
2. The nucleus is removed from the egg cell.
1. Female sheep A provides an egg cell.
16.在二项式定理这节教材中有这样一个性质: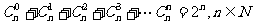
⑴计算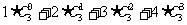 的值方法如下:
的值方法如下:
设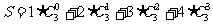
又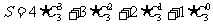
相加得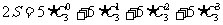
即
所以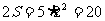 利用类似方法求值:
利用类似方法求值:  ⑵将⑴的情况推广到一般的结论,并给予证明
⑵将⑴的情况推广到一般的结论,并给予证明
⑶设 是首项为
是首项为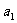 ,公比为
,公比为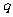 的等比数列
的等比数列 的前
的前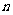 项的和,求
项的和,求
15.有这样一个事实:从装有6个球的口袋中取出2个球,共有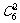 种取法。在这
种取法。在这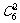 种取法中,可以分成一个指定的球被取到和未被取到两类:一类是该指定的球被取到,共有
种取法中,可以分成一个指定的球被取到和未被取到两类:一类是该指定的球被取到,共有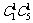 种取法;另一类是该指定的球未被取到,共有
种取法;另一类是该指定的球未被取到,共有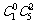 种取法。
⑴请从上述事实中提炼出一个有意义的等式;
⑵请写出⑴中等式的一般形式,使⑴中等式成为特例,并证明你写出的等式;
⑶根据题目中的事实,请你将⑵中的等式推广到更一般的形式,使⑵中等式成为特例,说明这个等式的实际意义,并证明这个等式。
种取法。
⑴请从上述事实中提炼出一个有意义的等式;
⑵请写出⑴中等式的一般形式,使⑴中等式成为特例,并证明你写出的等式;
⑶根据题目中的事实,请你将⑵中的等式推广到更一般的形式,使⑵中等式成为特例,说明这个等式的实际意义,并证明这个等式。
14.在中学阶段,对许多特定集合(如实数集、复数集以及平面向量集等)的学习常常是以定义运算(如四则运算)和研究运算律为主要内容.现设集合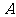 由全体二元有序实数组组成,在
由全体二元有序实数组组成,在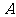 上定义一个运算,记为⊙,对于
上定义一个运算,记为⊙,对于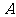 中的任意两个元素
中的任意两个元素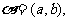
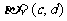 ,规定:
,规定: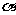 ⊙
⊙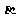
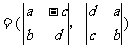 .
.
(Ⅰ)计算: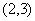 ⊙
⊙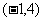 ;
;
(Ⅱ)请用数学符号语言表述运算⊙满足交换律和结合律,并任选其一证明;
(Ⅲ)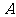 中是否存在唯一确定的元素
中是否存在唯一确定的元素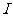 满足:对于任意
满足:对于任意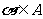 ,都有
,都有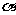 ⊙
⊙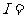
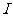 ⊙
⊙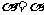 成立,若存在,请求出元素
成立,若存在,请求出元素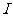 ;若不存在,请说明理由;
;若不存在,请说明理由;
(Ⅳ)试延续对集合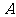 的研究,请在
的研究,请在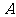 上拓展性地提出一个真命题,并说明命题为真的理由.
上拓展性地提出一个真命题,并说明命题为真的理由.
13. 杨辉是中国南宋末年的一位杰出的数学家、数学教育家、杨辉三角是杨辉的一大重要研究成果,它的许多性质与组合数的性质有关,杨辉三角中蕴藏了许多优美的规律。下图是一个11阶杨辉三角:
杨辉是中国南宋末年的一位杰出的数学家、数学教育家、杨辉三角是杨辉的一大重要研究成果,它的许多性质与组合数的性质有关,杨辉三角中蕴藏了许多优美的规律。下图是一个11阶杨辉三角:
 ⑴求第20行中从左到右的第4个数;
⑴求第20行中从左到右的第4个数;
⑵若第n行中从左到右第14与第15个数的比为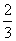 ,求n的值;
,求n的值;
⑶若n阶(包括0阶)杨辉三角的所有数的和;
⑷在第3斜列中,前5个数依次为1,3,6,10,15;第4斜列中,第5个数为35。显然,1+3+6+10+15=35。事实上,一般地有这样的结论:第m斜列中(从右上到左下)前k个数之和,一定等于第m+1斜列中第k个数。试用含有m、k 的数学公式表示上述结论,并给予证明。
的数学公式表示上述结论,并给予证明。
12.定义矩阵方幂运算:设A是一个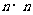 的矩阵,定义
的矩阵,定义 。若
。若 ,求⑴
,求⑴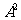 ,
, ;⑵猜测
;⑵猜测 ,并用数学归纳法证明。
,并用数学归纳法证明。
11.函数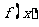 是这样定义的:对于任意整数
是这样定义的:对于任意整数 ,当实
,当实
数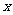 满足不等式
满足不等式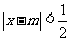 时,有
时,有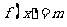 .
.
 ⑴求函数
⑴求函数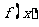 的定义域
的定义域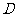 ,并画出它在
,并画出它在 上的图像;
上的图像;
 ⑵若数列
⑵若数列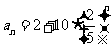 ,记
,记
 ,求
,求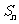 ;
;
⑶若等比数列 的首项是
的首项是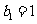 ,公比为
,公比为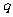 (q>0),
(q>0),
 又
又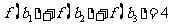 ,求公比
,求公比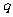 的取值范围.
的取值范围.
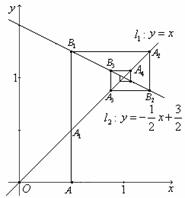
10、 如图所示,直线
如图所示,直线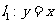 ,
,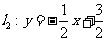 ,点
,点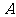 是
是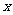 轴上的一点,过
轴上的一点,过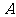 作
作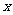 轴的垂线交
轴的垂线交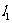 、
、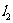 分别于
分别于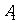 、
、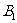 ,过
,过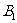 作
作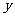 轴的垂线交
轴的垂线交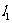 于
于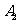 ,过
,过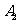 作
作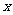 轴的垂线交
轴的垂线交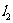 于
于 ……,依此类推分别作
……,依此类推分别作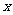 轴及
轴及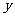 轴的垂线,这样在直线
轴的垂线,这样在直线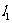 、
、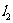 上分别得到点列
上分别得到点列 及
及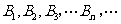 .设点
.设点 .
.
(1) 已知点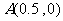 ,试写出数列
,试写出数列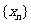 的递推关系式;
的递推关系式;
(2) 求数列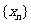 的通项公式,并计算
的通项公式,并计算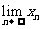 ;
;
(3) 考察(2)中的极限与两直线交点坐标之间的关系,试构造一个递推关系式并用计算器迭代求出方程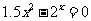 在区间
在区间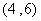 上的近似解(精确到0.01).
上的近似解(精确到0.01).
9. 设函数
设函数 ,其中
,其中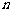 为正整数.⑴判断函数
为正整数.⑴判断函数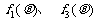 的单调性,并就
的单调性,并就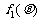 的情形证明你的结论;⑵证明:
的情形证明你的结论;⑵证明: ;
;
⑶对于任意给定的正整数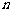 ,求函数
,求函数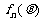 的最大值和最小值.
的最大值和最小值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com