
41.(上海理综)中国馆、世博中心和主题馆等主要场馆,太阳能的利用规模达到了历届世博会之最,总发电装机容量达到4.6×103kW。设太阳能电池板的发电效率为18%,已知地球表面每平方米接收太阳能的平均辐射功率为1.353kW,那么所使用的太阳能电池板的总面积为 m2。
答案:1.9×1014
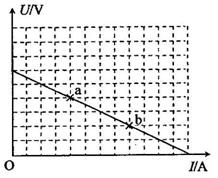
19.(新课标卷)电源的效率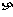 定义为外电路电阻消耗的功率与电源的总功率之比.在测电源电动势和内电阻的实验中得到的实验图线如图所示,图中U为路端电压,I为干路电流,a、b为图线上的两点,相应状态下电源的效率分别为
定义为外电路电阻消耗的功率与电源的总功率之比.在测电源电动势和内电阻的实验中得到的实验图线如图所示,图中U为路端电压,I为干路电流,a、b为图线上的两点,相应状态下电源的效率分别为 、
、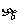 .由图可知
.由图可知 、
、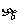 的值分别为
的值分别为
A、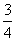 、
、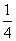 B、
B、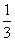 、
、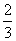 C、
C、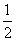 、
、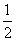 D、
D、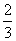 、
、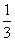
答案:D
解析:电源效率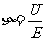 ,E为电源的总电压(即电动势),根据图象可知Ua=
,E为电源的总电压(即电动势),根据图象可知Ua=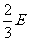
Ub=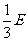 ,所以选项D正确。
,所以选项D正确。
2. (2010福建理数)
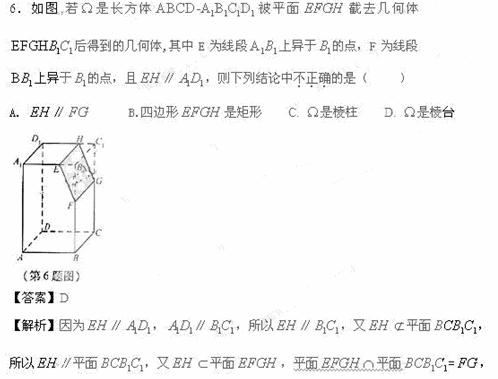
所以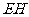 ∥
∥ ,故
,故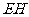 ∥
∥ ∥
∥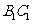 ,所以选项A、C正确;因为
,所以选项A、C正确;因为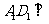 平面
平面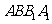 ,
,
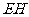 ∥
∥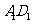 ,所以
,所以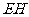
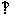 平面
平面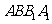 ,又
,又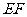
 平面
平面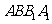 ,
故
,
故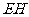
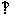
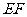 ,所以选项B也正确,故选D。
,所以选项B也正确,故选D。
[命题意图]本题考查空间中直线与平面平行、垂直的判定与性质,考查同学们的空间想象能力和逻辑推理能力。
8.C
[解析]该几何体由两个长方体组合而成,其表面积等于下面长方体的全面积加上面长方体的4个侧面积之和。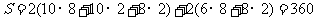 .
.
[方法技巧]把三视图转化为直观图是解决问题的关键.又三视图很容易知道是两个长方体的组合体,画出直观图,得出各个棱的长度.把几何体的表面积转化为下面长方体的全面积加上面长方体的4个侧面积之和。
1.(2010安徽理数)8、一个几何体的三视图如图,该几何体的表面积为
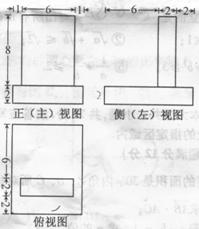 A、280 B、292 C、360 D、372
A、280 B、292 C、360 D、372
4.(2010湖北文数)用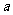 、
、 、
、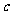 表示三条不同的直线,
表示三条不同的直线,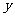 表示平面,给出下列命题:
表示平面,给出下列命题:
①若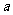 ∥
∥ ,
, ∥
∥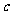 ,则
,则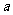 ∥
∥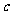 ;②若
;②若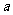 ⊥
⊥ ,
, ⊥
⊥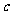 ,则
,则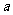 ⊥
⊥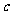 ;
;
③若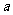 ∥
∥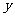 ,
, ∥
∥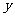 ,则
,则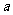 ∥
∥ ;④若
;④若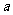 ⊥
⊥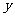 ,
, ⊥
⊥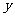 ,则
,则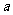 ∥
∥ .
.
A. ①② B. ②③ C. ①④ D.③④

(2010山东理数)(3)在空间,下列命题正确的是
(A)平行直线的平行投影重合
(B)平行于同一直线的两个平面平行
(C)垂直于同一平面的两个平面平行
(D)垂直于同一平面的两条直线平行
[答案]D
[解析]由空间直线与平面的位置关系及线面垂直与平行的判定与性质定理可以得出答案。
[命题意图]考查空间直线与平面的位置关系及线面垂直与平行的判定与性质,属基础题。
6.C[命题意图]本小题主要考查直三棱柱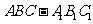 的性质、异面直线所成的角、异面直线所成的角的求法.
的性质、异面直线所成的角、异面直线所成的角的求法.
[解析]延长CA到D,使得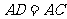 ,则
,则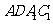 为平行四边形,
为平行四边形,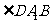 就是异面直线
就是异面直线
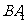 与
与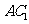 所成的角,又三角形
所成的角,又三角形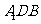 为等边三角形,
为等边三角形,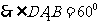
(2010全国卷1理数)(12)已知在半径为2的球面上有A、B、C、D四点,若AB=CD=2,则四面体ABCD的体积的最大值为
(A) 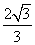 (B)
(B)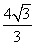 (C)
(C) 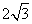 (D)
(D) 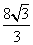

(2010全国卷1理数)(7)正方体ABCD-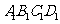 中,B
中,B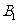 与平面AC
与平面AC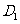 所成角的余弦值为
所成角的余弦值为
(A) 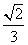 (B)
(B)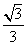 (C)
(C)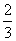 (D)
(D)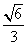

(2010四川文数)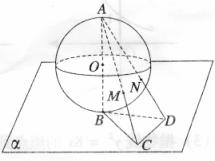 (12)半径为
(12)半径为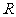 的球
的球 的直径
的直径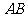 垂直于平面
垂直于平面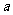 ,垂足为
,垂足为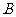 ,
,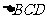 是平面
是平面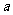 内边长为
内边长为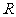 的正三角形,线段
的正三角形,线段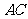 、
、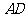 分别与球面交于点
分别与球面交于点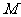 、
、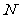 ,那么
,那么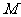 、
、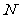 两点间的球面距离是
两点间的球面距离是
(A)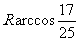 (B)
(B)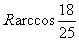
(C)
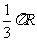 (D)
(D)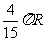
解析:由已知,AB=2R,BC=R,故tan∠BAC=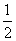
cos∠BAC=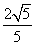
连结OM,则△OAM为等腰三角形
AM=2AOcos∠BAC=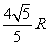 ,同理AN=
,同理AN=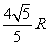 ,且MN∥CD
,且MN∥CD
而AC=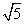 R,CD=R
R,CD=R
故MN:CD=AN:AC
Þ MN=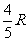 ,
,
连结OM、ON,有OM=ON=R
于是cos∠MON=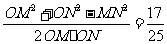
所以M、N两点间的球面距离是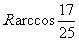
答案:A
9.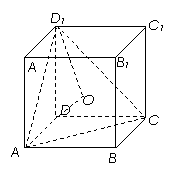 D [命题意图]本小题主要考查正方体的性质、直线与平面所成的角、点到平面的距离的求法,利用等体积转化求出D到平面AC
D [命题意图]本小题主要考查正方体的性质、直线与平面所成的角、点到平面的距离的求法,利用等体积转化求出D到平面AC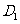 的距离是解决本题的关键所在,这也是转化思想的具体体现.
的距离是解决本题的关键所在,这也是转化思想的具体体现.
[解析1]因为BB1//DD1,所以B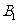 与平面AC
与平面AC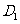 所成角和DD1与平面AC
所成角和DD1与平面AC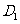 所成角相等,设DO⊥平面AC
所成角相等,设DO⊥平面AC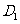 ,由等体积法得
,由等体积法得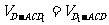 ,即
,即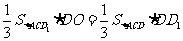 .设DD1=a,
.设DD1=a,
则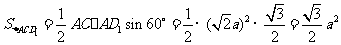 ,
,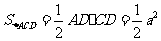 .
.
所以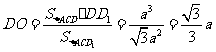 ,记DD1与平面AC
,记DD1与平面AC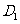 所成角为
所成角为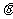 ,则
,则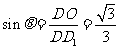 ,所以
,所以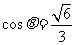 .
.
[解析2]设上下底面的中心分别为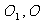 ;
;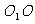 与平面AC
与平面AC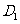 所成角就是B
所成角就是B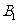 与平面AC
与平面AC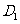 所成角,
所成角,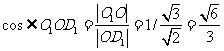
(2010全国卷1文数)(6)直三棱柱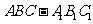 中,若
中,若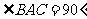 ,
,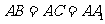 ,则异面直线
,则异面直线
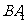 与
与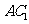 所成的角等于
所成的角等于
(A)30° (B)45°(C)60° (D)90°
12.B[命题意图]本小题主要考查几何体的体积的计算、球的性质、异面直线的 距离,通过球这个载体考查考生的空间想象能力及推理运算能力.
距离,通过球这个载体考查考生的空间想象能力及推理运算能力.
[解析]过CD作平面PCD,使AB⊥平面PCD,交AB与P,设点P到CD的距离为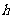 ,则有
,则有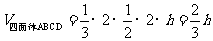 ,当直径通过AB与CD的中点时,
,当直径通过AB与CD的中点时,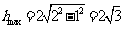 ,故
,故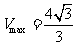
(2010全国卷1文数)(9)正方体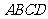 -
-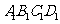 中,
中,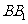 与平面
与平面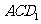 所成角的余弦值为
所成角的余弦值为
(A) 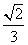 (B)
(B)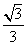 (C)
(C)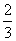 (D)
(D)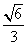
6.D.
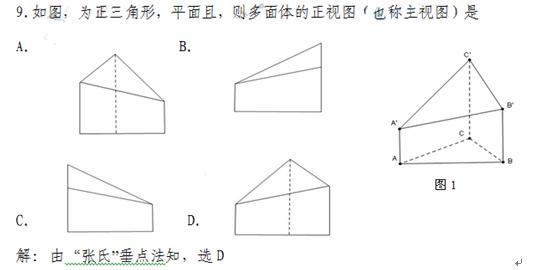
(2010广东文数)
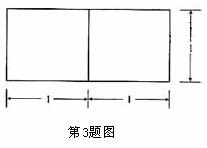 (2010福建文数)3.若一个底面是正三角形的三棱柱的正视图如图所示,则其侧面积等于 ( )
(2010福建文数)3.若一个底面是正三角形的三棱柱的正视图如图所示,则其侧面积等于 ( )
A. B.2
B.2
C.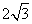 D.6
D.6
[答案]D
[解析]由正视图知:三棱柱是以底面边长为2,高为1的正三棱柱,所以底面积为
 ,侧面积为
,侧面积为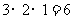 ,选D.
,选D.
[命题意图]本题考查立体几何中的三视图,考查同学们识图的能力、空间想象能力等基本能力。
(2010全国卷1文数)(12)已知在半径为2的球面上有A、B、C、D四点,若AB=CD=2,则四面体ABCD的体积的最大值为
(A) 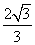 (B)
(B)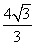 (C)
(C) 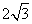 (D)
(D) 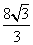
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com