
4、[答案]C
[命题意图]本题从分段函数的角度出发,考查了学生对基本初等函数的掌握程度。
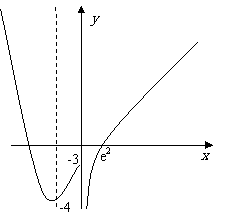
[解析]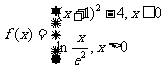 ,绘制出图像大致为
,绘制出图像大致为
所以零点个数为2。
3、[答案]A
[命题意图]本题考查学生对等差数列公式、求和公式的掌握程度,以及一元二次方程最值问题的求解。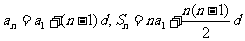 。
。
 [解析]由
[解析]由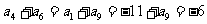 ,得到
,得到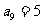 ,从而
,从而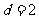 ,所以
,所以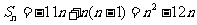 ,因此当
,因此当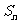 取得最小值时,
取得最小值时,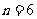 .
.
2、[答案]D
[命题意图] 本题考查学生对抛物线焦点的识记以及原方程的求解。
本题考查学生对抛物线焦点的识记以及原方程的求解。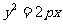 的焦点为
的焦点为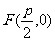 ,求解圆方程时,确定了圆
,求解圆方程时,确定了圆 心与半径就好做了。
心与半径就好做了。
[解析]抛物线的焦点为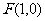 ,又圆过原点,所以
,又圆过原点,所以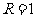 ,方程为
,方程为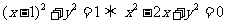 。
。
1、[答案]A
[命题意图]本题考查学生对于三角两角差公式的运用以及常见三角函数值的记忆。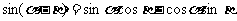 ,
,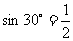 。
。
[解析]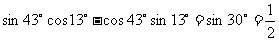
21.本题设有(1)(2)(3)三个选考题,每题7分,请考生任选2题作答,满分14分。如果多做,则按所做的前两题记分。作答时,先用2B铅笔在答题卡上把所选题目对应的题号涂黑,并将所选题号填入括号中。
(1)(本小题满分7分)选修4-2:矩阵与变换
已知矩阵M=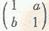 ,N=
,N=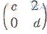 ,且MN=
,且MN= 。
。
(Ⅰ)求实数a,b,c,d的值;(Ⅱ)求直线y=3x在矩阵M所对应的线性变换作用下的像的方程。
(2)(本小题满分7分)选修4-4:坐标系与参数方程
在直角坐标系xOy中,直线L的参数方程为 (t为参数),在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为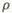 =2
=2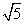 sin
sin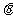 。
。
(Ⅰ)求圆C的直角坐标方程;
(Ⅱ)设圆C与直线L交于点A,B。若点P的坐标为(3,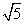 ),求∣PA∣+∣PB∣。
),求∣PA∣+∣PB∣。
(3)(本小题满分7分)选修4-5:不等式选讲
已知函数f(x)= ∣x-a∣.
(Ⅰ)若不等式f(x)  3的解集为
3的解集为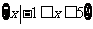 ,求实数a的值;
,求实数a的值;
(Ⅱ)在(Ⅰ)的条件下,若f(x)+f(x+5)≥m对一切实数x恒成立,求实数m的取值范围。
[2010年福建高考试题解析](理科数学)
20.(本小题满分14分)
(Ⅰ)已知函数f(x)=x3-x ,其图像记为曲线C.
(i) 求函数f(x)的单调区间;
(ii)
证明:若对于任意非零实数x1 ,曲线C与其在点P1
(x1,f(x1)))处的切线交于另一点P2(x2,f(x2)),曲线C与其在点P2处的切线交于另一点P3(x3,f(x3)),线段P1 P2, P2 P3与曲线C所围成封闭图形的面积分别记为S1,S2,则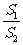 为定值;
为定值;
(Ⅱ)对于一般的三次函数g(x)=ax3+bx2+cx+d(a 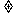 0),请给出类似于(Ⅰ)(ii)的正确命题,并予以证明。
0),请给出类似于(Ⅰ)(ii)的正确命题,并予以证明。
19.(本小题满分13分)
某港口O要将一件重要物品用小艇送到一艘正在航行的轮船上,在小艇出发时,轮船位于港口O北偏西30°且与该港口相距20海里的A处,并正以30海里/小时的航行速度沿正东方向匀速行驶,经过t小时与轮船相遇。
(Ⅰ)若希望相遇时小艇的航行距离最小,则小艇航行速度的大小应为多少?
(Ⅱ)假设小艇的最高航行速度只能达到30海里/小时,试设计航行方案(即确定航行方向和航行速度的大小),使得小艇能以最短时间与轮船相遇,并说明理由。
18.(本小题满分13分)
如图,圆柱OO1内有一个三棱柱ABC-A1B1C1,
三棱柱的底面为圆柱底面的内接三角形,且AB是圆O的直径。
(Ⅰ)证明:平面A1ACC1⊥平面B1BCC1;
(Ⅱ)设AB=AA1。在圆柱OO1内随机选取一点,记该点取自于
三棱柱ABC-A1B1C1内的概率为P。
(i) 当点C在圆周上运动时,求P的最大值;
(ii)
记平面A1ACC1与平面B1OC所成的角为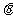 (0°<
(0°< 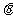
 90°)。当P取最大值时,求cos
90°)。当P取最大值时,求cos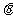 的值。
的值。
17.(本小题满分13分)
已知中心在坐标原点O的椭圆C经过点A(2,3),且点F(2.0)为其右焦点。
(Ⅰ)求椭圆C的方程;
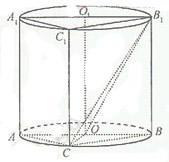 (Ⅱ)是否存在平行于OA的直线L,使得直线L与椭圆C有公共点,且直线OA与L的距离等于4?若存在,求出直线L的方程;若不存在,说明理由。
(Ⅱ)是否存在平行于OA的直线L,使得直线L与椭圆C有公共点,且直线OA与L的距离等于4?若存在,求出直线L的方程;若不存在,说明理由。
16.(本小题满分13分)
设S是不等式x2-x-6 0的解集,整数m,n
0的解集,整数m,n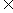 S。
S。
(Ⅰ)记“使得m+n=0成立的有序数组(m,n)”为事件A,试列举A包含的基本事件;
(Ⅱ)设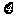 =m2,求
=m2,求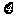 的分布列及其数学期望E
的分布列及其数学期望E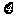 。
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com