
8. 下列有关化学研究的正确说法是
A.同时改变两个变量来研究反映速率的变化,能更快得出有关规律
B.对于同一个化学反应,无论是一步完成还是分几步完成,其反应的焓变相同
C.依据丁大尔现象可将分散系分为溶液、胶体与浊液
D.从HF、HCl、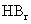 、HI酸性递增的事实,推出F、Cl、Br、I的非金属递增的规律
、HI酸性递增的事实,推出F、Cl、Br、I的非金属递增的规律
[解析]答案:B
本题侧重考查反应速率、盖斯定律、分散系、元素周期律重要的基本概念,规律
A. 同时改变两个变量来研究反应速率的变化,不容易判断影响反应速率的主导因素,因此更难得出有关规律
B. 这是盖斯定律的表述
C. 分散系的划分是以分散质颗粒大小来区分的
D. 在以酸性强弱作为判断元素非金属性非金属性强弱依据时,是以最高价氧化物对应水化物的酸性强弱为判断依据的。
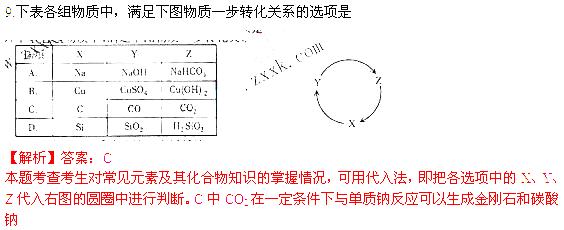
7.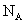 表示阿伏伽德罗常数,下列判断正确的是
表示阿伏伽德罗常数,下列判断正确的是
A.在18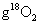 中含有
中含有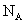 个氧原子
个氧原子
B.标准状况下,22.4L空气含有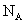 个单质分子
个单质分子
C.1 mol参加反应转移电子数一定为2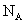
D.含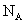 个
个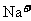 的
的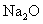 溶解于1L水中,
溶解于1L水中,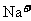 的物质的量浓度为
的物质的量浓度为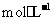

6.下列关于有机物的正确说法是
A.聚乙烯可发生加成反应 B。石油干馏可得到汽油、,煤油等。
C.淀粉、蛋白质完全水解的产物互为同分异构体 D。乙酸乙酯、油脂与NaOH溶液反
应均有醇生成。
[解析]答案:D
本题考查有机化学方面有关的知识点
A. 乙烯加聚反应生成聚乙烯后,双键变单键不能发生加成反应
B. 石油分馏可得汽油和煤油属于物理变化过程,干馏是指隔绝空气加强热,属于化学变化
C. 淀粉属于糖类,完全水解生成葡萄糖;蛋白质完全水解生成氨基酸;两者的产物不可能是同分异构体
D. 乙酸乙酯和油脂都属于酯类,在氢氧化钠溶液反应后均生成醇,前者生成乙醇,后者生成甘油
21、(1)(矩阵变换)[解析](1) ,对应系数有
,对应系数有 ;(2)取
;(2)取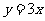 上一点
上一点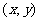 ,设经过变换后对应点为
,设经过变换后对应点为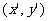 ,则
,则 ,从而
,从而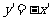 ,所以经过变换后的图像方程为
,所以经过变换后的图像方程为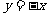 。
。
[命题意图]本题考查的是学生对矩阵运算理解与掌握,要求考生能够正确进行运算,熟悉矩阵的基本运算方法。
[点评]本题相对基础,对于学生提高自信心有一定帮助。
(2)(坐标系与参数方程)[解析](1)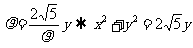 ,所以
,所以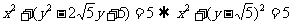 ;(2)直线的一
;(2)直线的一 般方程为
般方程为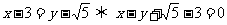 ,容易知道P在直线上,又
,容易知道P在直线上,又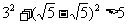 ,所以P在圆外,联立圆与直线方程可以得到:
,所以P在圆外,联立圆与直线方程可以得到: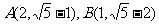 ,所以|PA|+|
,所以|PA|+| PB|=|AB|+2|PA|=
PB|=|AB|+2|PA|=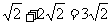 ,所以答案为
,所以答案为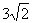
[命题意图]本题考查了学生极坐标方程化一般方程、参数方程化一般方程的能力以及综合的分析问题能力,有一定的选拔意义。
[ 点评]遇到参数方程题目的时候,只需要化简为一般方程,问题便迎刃而解。
点评]遇到参数方程题目的时候,只需要化简为一般方程,问题便迎刃而解。
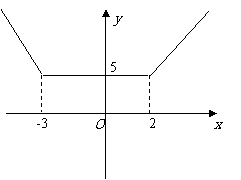 (3)(不等式选讲)[解析]
(3)(不等式选讲)[解析] ,对应系数得a=2;(2)
,对应系数得a=2;(2)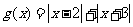 的图像为
的图像为
所以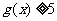 ,故
,故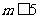 。
。
[命题意图]本题考查学生解不等式的基本能力,难度较低。
[点评]本类型的方法是绘图法,或者采用零点分区间法,考查基本。
20、[解析](1)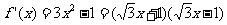 ,令
,令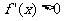 得到
得到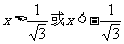 ,令
,令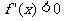 有
有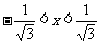 ,因此原函数的单调递增区间为
,因此原函数的单调递增区间为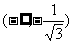 和
和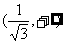 ;单调递减区间为
;单调递减区间为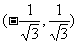
(2)(i)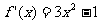 ,
,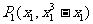 ,
, ,因此过点
,因此过点 的切线方程为:
的切线方程为: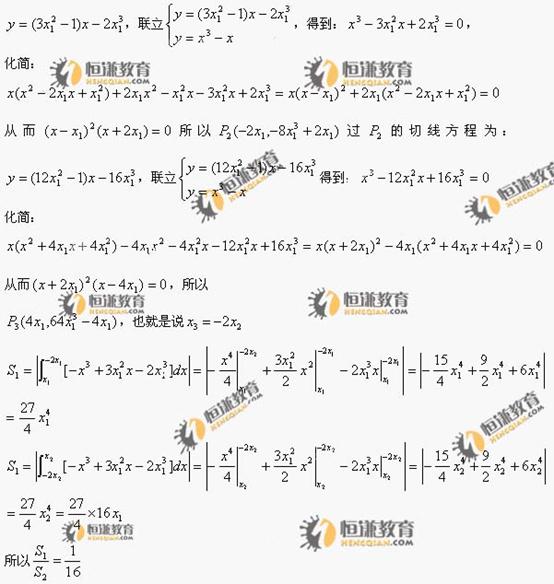 (ii)[命题]若对于任意函数
(ii)[命题]若对于任意函数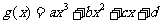 的图像为曲线
的图像为曲线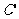 ,其类似于(2)(i)的命题为:若对任意不等于
,其类似于(2)(i)的命题为:若对任意不等于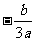 的实数
的实数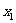 ,曲线与其在点
,曲线与其在点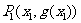 处的切线交于另一点
处的切线交于另一点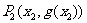 ,曲线
,曲线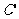 与其在点
与其在点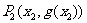 处的切线交于另外一点
处的切线交于另外一点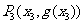 ,线段
,线段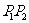 、
、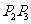 与曲线
与曲线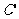 所围成面积为
所围成面积为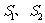 ,则
,则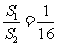 。
。
[证明]对于曲线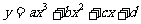 ,无论如何平移,其面积值是恒定的,所以这里仅考虑
,无论如何平移,其面积值是恒定的,所以这里仅考虑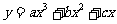 的情形,
的情形,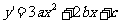 ,
,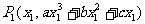 ,
,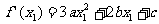 ,因此过点
,因此过点 的切线方程为:
的切线方程为:
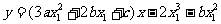 ,联立
,联立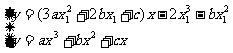 ,得到:
,得到: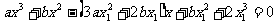 ,
,
化简:得到
从而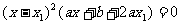 所以
所以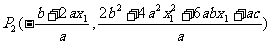 同样运用(i)中方法便可以得到
同样运用(i)中方法便可以得到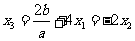
所以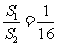
[命题意图]本题从函数角度出发,考查了积分运算、单调性、求导等基本能力,又综合地考查了学生分析问题、解决问题的能力。计算量较大,不容易正确。
[点评]该题思维量较小,计算量却较为庞大,对考生有一定的区分作用。
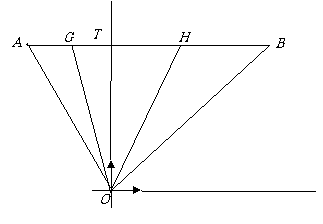
19、[解析](1)为使小艇航行距离最短,理想化的航行路线为OT,小艇到达T位置时轮船的航行位移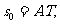 即
即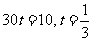 ,
,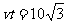 ,从而
,从而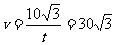 (海里/时)
(海里/时)
(2)讨论:(1)若轮船与小艇在A、T之间G位置相遇时,根据小艇的速度限制,有OG<AG,但实际上,这种情况中AG<OG,所以不符合要求舍去。轮船与小艇的交点必在T、B之间。
(2)若轮船与小艇在H处相遇时,在直角三角形OHT中运用勾股定理有: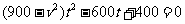 ,等价于
,等价于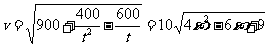
 从而
从而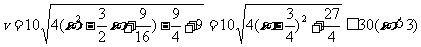
所以当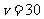 时,
时,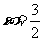 ,
,
也就是说,当小艇以30海里每小时的速度,沿北偏东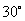 方向行走能以最短的时间遇到轮船。
方向行走能以最短的时间遇到轮船。
[命题意图]本题从三角函数出发,考查了学生运用知识解决实际问题的能力、求解一元二次方程最值问题的能力以及综合分析问题的能力。
[点评]对待应用题没有什么通解通法,只要你不畏惧困难,认真读题、审题,通过列表、作图等方式合理分析已知量间的关系,总是能够轻松解题。
16、[解析](1)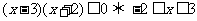 ,则
,则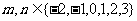
 有
有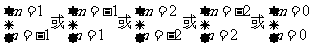 ,因此A包含的基本事件为:
,因此A包含的基本事件为: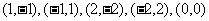
(2)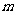 的可能去取为
的可能去取为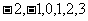 ,则
,则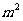 的可能取值为
的可能取值为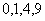
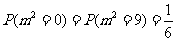 ,
,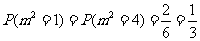
因此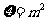 得分布列为:
得分布列为:
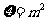 |
0 |
1 |
4 |
9 |
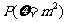 |
 |
 |
 |
 |
数学期望为

[命题意图]本题考查学生对概率分布的理解以及数学期望的计算,难度较易。
[点评]本题作为解答题的第一题具备送分的作用,考生只要掌握了基本的计算知识,能够轻松应对。
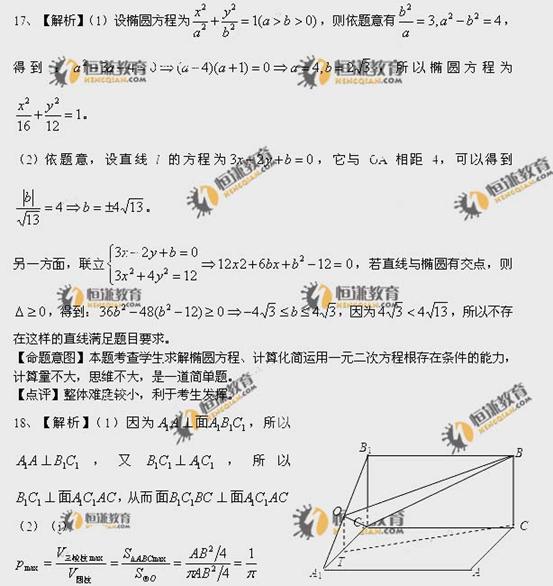
(ii)过O点做OT平行于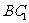 ,则由
,则由 有
有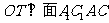 ,所以
,所以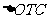 即为面
即为面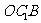 在
在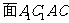 内的投影,设
内的投影,设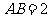 ,则
,则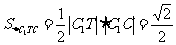 ,设二面角
,设二面角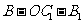 的平面角大小为
的平面角大小为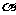 ,则
,则
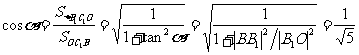
从而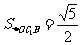 ,故
,故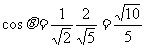
[命题意图]本题从棱柱出发,综合地考查了学生线面垂直、面面垂直的证明方法以及二面角、简单概率的求解,综合性强,灵活度大,是一道较好的题目。
[点评]在完成立体几何题目时,考生应当尽量把握从已知到未知的推理,发挥自己的空间思维能力,转化图形。正确求解。
11、[答案]124
[命题意图]本题通过抽象函数,考查了函数的周期性,单调性,以及学生的综合分析能力,难度不大。
[解析]1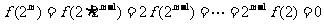 ,正确;2取
,正确;2取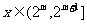 ,则
,则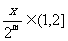 ;
;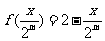 ,从而
,从而
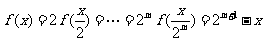 ,其中,
,其中,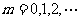 ,从而
,从而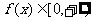 ,正确;3
,正确;3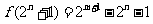 ,假设存在
,假设存在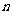 使
使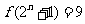 ,即存在
,即存在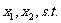
 ,又,
,又,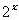 变化如下:2,4,8,16,32,……,显然不存在,所以该命题错误;4根据前面的分析容易知道该选项正确;综合有正确的序号是124
变化如下:2,4,8,16,32,……,显然不存在,所以该命题错误;4根据前面的分析容易知道该选项正确;综合有正确的序号是124
6、[答案]D
[命题意图]本题考查考生对立体几何体的理解程度、空间想像能力。灵活,全面地考查了考生对知识的理解。
[解析]若FG不平行于EH,则FG与EH相交,焦点必 然在B1C1上,而EH平行于B1C1,矛盾,所以FG平行于EH;由
然在B1C1上,而EH平行于B1C1,矛盾,所以FG平行于EH;由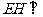 面
面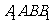 ,得到
,得到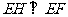 ,可以得到四边形EFGH为矩形,将
,可以得到四边形EFGH为矩形,将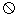 从正面看过去,就知道是一个五棱柱,C正确;D没能正确理解棱台与这个图形。
从正面看过去,就知道是一个五棱柱,C正确;D没能正确理解棱台与这个图形。
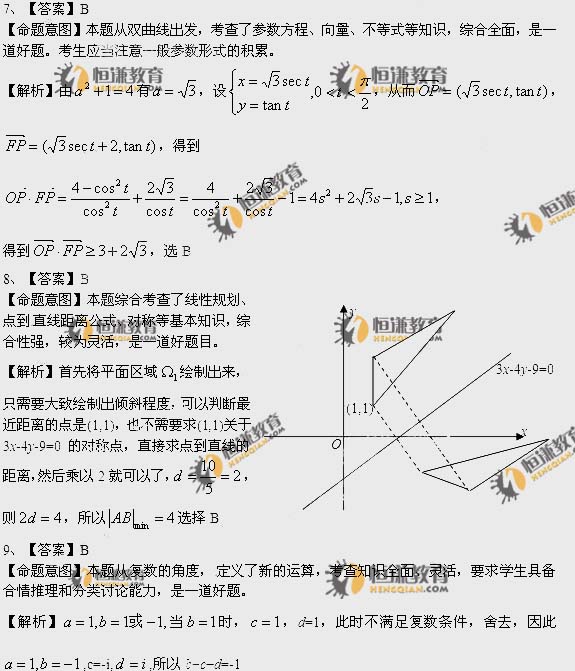 [答案]C
[答案]C
[命题意图]本题从大学数列极限定义的角度出发,仿造构造了分渐近线函数,目的是考查学生分析问题、解决问题的能力,考生需要抓住本质:存在分渐近线的充要条件是 时,
时, 进行做答,是一道好题,思维灵活。
进行做答,是一道好题,思维灵活。
[解析]要透过现象看本质,存在分渐近线的充要条件是 时,
时, 。对于1,当
。对于1,当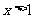 时便不符合,所以1不存在;对于2,肯
时便不符合,所以1不存在;对于2,肯 定存在分渐近线,因为当时,
定存在分渐近线,因为当时, ;对于3,
;对于3,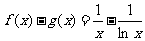 ,设
,设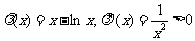 且
且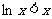 ,所以当
,所以当 时
时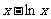 越来愈大,从而
越来愈大,从而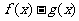 会越来越小,不会趋近于0,所以不存在分渐近线;4当
会越来越小,不会趋近于0,所以不存在分渐近线;4当 时,
时,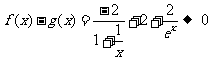 ,因此存在分渐近线。故,存在分
,因此存在分渐近线。故,存在分 渐近线的是24选C
渐近线的是24选C

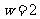 ,得到
,得到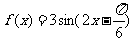 ,当
,当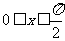 时,
时, ,所以
,所以
5、[答案]C
[命题意图]本题考查学生对程序框图的理解。选材较为简单,只需要考生能从上到下一步步列出就可以正确作答。
[ 解析]s=0
解析]s=0 i=1
i=1 a=2
a=2
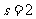

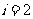

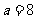

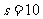

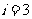

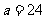

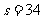
 i=4
i=4 输出i=4,选择C
输出i=4,选择C
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com