
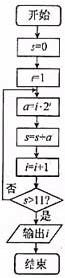
4.函数f(x)= 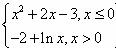 的零点个数为
的零点个数为
A. 0 B. 1 C.2 D.3
3.设等差数列{an}前n项和为Sn . 若a1= -11,a4+a6= -6 ,则当Sn 取最小值时,n等于
 A.6
B. 7
C.8 D.9
A.6
B. 7
C.8 D.9
2.以抛物线y2=4x的焦点为圆心,且过坐标原点的圆的方程为
A. x2+y2+2x=0 B. x2+y2+x=0
C. x2+y2-x=0 D. x2+y2-2x=0
1.计算sin43°cos13°-cos43°sin13°的结果等于
A.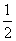 B.
B. 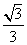 C.
C.
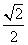 D.
D. 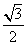
22.(本小题满分14分)
已知函数f(x)=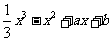 的图像在点P(0,f(0))处的切线方程为y=3x-2
的图像在点P(0,f(0))处的切线方程为y=3x-2
(Ⅰ)求实数a,b的值;
(Ⅱ)设g(x)=f(x)+ 是[
是[ ]上的增函数。
]上的增函数。
(i)求实数m的最大值;
(ii)当m取最大值时,是否存在点Q,使得过点Q的直线若能与曲线y=g(x)围成两个封闭图形,则这两个封闭图形的面积总相等?若存在,求出点Q的坐标;若不存在,说明理由。




21.(本小题满分12分)
某港口 要将一件重要物品用小艇送到一艘正在航行的轮船上,在小艇出发时,轮船位于港口
要将一件重要物品用小艇送到一艘正在航行的轮船上,在小艇出发时,轮船位于港口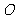 北偏西30°且与该港口相距20海里的
北偏西30°且与该港口相距20海里的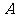 处,并正以30海里/小时的航行速度沿正东方向匀速行驶。假设该小艇沿直线方向以
处,并正以30海里/小时的航行速度沿正东方向匀速行驶。假设该小艇沿直线方向以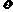 海里/小时的航行速度匀速行驶,经过
海里/小时的航行速度匀速行驶,经过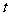 小时与轮船相遇。
小时与轮船相遇。
(Ⅰ)若希望相遇时小艇的航行距离最小,则小艇航行速度的大小应为多少?
(Ⅱ)为保证小艇在30分钟内(含30分钟)能与轮船相遇,试确定小艇航行速度的最小值; (Ⅲ)是否存在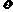 ,使得小艇以
,使得小艇以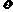 海里/小时的航行速度行驶,总能有两种不同的航行方向与轮船相遇?若存在,试确定
海里/小时的航行速度行驶,总能有两种不同的航行方向与轮船相遇?若存在,试确定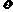 的取值范围;若不存在,请说明理由。
的取值范围;若不存在,请说明理由。

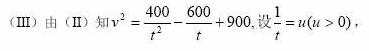

20. (本小题满分12分)
如图,在长方体ABCD – A1B1C1D1中,E,H分别是棱A1B1,D1C1上的点(点E与B1不重合),且EH//A1D1。过EH的平面与棱BB1,CC1相交,交点分别为F,G。
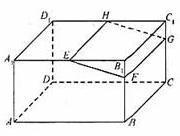 (I)证明:AD//平面EFGH;
(I)证明:AD//平面EFGH;
(II)设AB=2AA1=2a。在长方体ABCD-A1B1C1D1内随机选取一点,记该点取自于几何体A1ABFE – D1DCGH内的概率为p。当点E,F分别在棱A1B1, B1B上运动且满足EF=a时,求p的最小值。


19.(本小题满分12分)
已知抛物线C: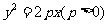 过点A (1 , -2)。
过点A (1 , -2)。
(I)求抛物线C 的方程,并求其准线方程;
(II)是否存在平行于OA(O为坐标原点)的直线L,使得直线L与抛物线C有公共点,且直线OA与L的距离等于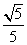 ?若存在,求直线L的方程;若不存在,说明理由。
?若存在,求直线L的方程;若不存在,说明理由。

18.(本小题满分12分)
设平顶向量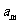 = ( m , 1),
= ( m , 1), 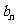 = ( 2 , n ),其中 m, n
= ( 2 , n ),其中 m, n 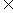 {1,2,3,4}.
{1,2,3,4}.
(I)请列出有序数组( m,n )的所有可能结果;
(II)记“使得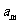
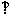 (
(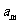 -
-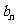 )成立的( m,n )”为事件A,求事件A发生的概率。
)成立的( m,n )”为事件A,求事件A发生的概率。

17. (本小题满分12分 )
数列{ } 中
} 中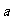 =
=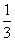 ,前n项和
,前n项和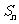 满足
满足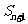 -
-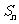 =
=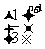 (n
(n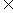
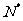 ).
).
( I ) 求数列{ }的通项公式
}的通项公式 以及前n项和
以及前n项和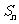 ;
;
(II)若S1, t ( S1+S2 ), 3( S2+S3 ) 成等差数列,求实数t的值。

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com