
5.伯里克利说:民主的实质就是“政权在全体公民手中,而不是在少数人手中”。他在担任首席将军时雅典民主政治的新发展表现在 ( )
①设立五百人会议 ②成年男性公民都可以参加公民大会
③给低等级的公民参加政治活动发放津贴④创立“陶片放逐法”
A.①②④ B.②③④ C.①④ D.②③
 6.右图中的十二块铜牌陈列于罗马广场,详细列出了民法、
6.右图中的十二块铜牌陈列于罗马广场,详细列出了民法、
刑法、诉讼程序等许多方面的内容。此举的历史意义
在于 ( )
A.应广大平民要求设立
B.保障了平民利益,消除了平民与贵族的矛盾
C.用文字明示法律规定,成为罗马法发展的里程碑
D.作为罗马的基本法,标志着罗马法的成熟
4.史载:“自雍乾后百八十年,威命所寄,不于内阁而于军机处。”这一变化 ( )
A.提高了清朝行政效率 B.消除了皇权相权矛盾
C.扩大了清朝统治基础 D.增加了政务处理环节
3.斯塔夫里阿诺斯在《全球通史》中说:“在中国长达数千年的历史上,有过三次大革命,它们从根本上改变了中国的政治和社会结构/第一次发生于公元前221年……第二次发生于1911年……第三次在1949年”。第一次“革命”是指 ( )
A.中央集权制度建立 B.世袭制度确立
C.宗法式家族制度形成 D.世卿世禄制度确立
2.《史记·楚世家》记载:“(春秋时期楚庄王)八年,伐陆军戎(在洛阳西南),遂至洛,观兵于周郊。周定王使王孙满劳楚王。楚王问鼎大小轻重。”这则材料突出反映了当时
( )
A.王权衰落,王命不行 B.尊王攘夷,天子独尊
C.周室衰微,大国争霸 D.列国内乱,诸侯兼并
1.西周时期实行宗法制度到春秋时期逐渐松驰,由此产生的主要政治影响是 ( )
A.世卿世禄的特权自行消亡 B.土地国有制度逐渐被废止
C.中央对地方的控制削弱 D.贵族阶层逐渐转化为庶民
功率是描述做功快慢的物理量。
(1)功率的定义式: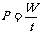 ,所求出的功率是时间t内的平均功率。
,所求出的功率是时间t内的平均功率。
(2)功率的计算式:P=Fvcosθ,其中θ是力与速度间的夹角。该公式有两种用法:①求某一时刻的瞬时功率。这时F是该时刻的作用力大小,v取瞬时值,对应的P为F在该时刻的瞬时功率;
②当v为某段位移(时间)内的平均速度时,则要求这段位移(时间)内F必须为恒力,对应的P为F在该段时间内的平均功率。
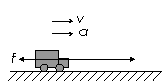 ⑶重力的功率可表示为PG=mgvy,即重力的瞬时功率等于重力和物体在该时刻的竖直分速度之积。
⑶重力的功率可表示为PG=mgvy,即重力的瞬时功率等于重力和物体在该时刻的竖直分速度之积。
⑷汽车的两种加速问题。当汽车从静止开始沿水平面加速运动时,有两种不同的加速过程,但分析时采用的基本公式都是P=Fv和F-f = ma
①恒定功率的加速。由公式P=Fv和F-f=ma知,由于P恒定,随着v的增大,F必将减小,a也必将减小,汽车做加速度不断减小的加速运动,直到F=f,a=0,这时v达到最大值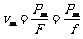 。可见恒定功率的加速一定不是匀加速。这种加速过程发动机做的功只能用W=Pt计算,不能用W=Fs计算(因为F为变力)。
。可见恒定功率的加速一定不是匀加速。这种加速过程发动机做的功只能用W=Pt计算,不能用W=Fs计算(因为F为变力)。
②恒定牵引力的加速。由公式P=Fv和F-f=ma知,由于F恒定,所以a恒定,汽车做匀加速运动,而随着v的增大,P也将不断增大,直到P达到额定功率Pm,功率不能再增大了。这时匀加速运动结束,其最大速度为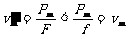 ,此后汽车要想继续加速就只能做恒定功率的变加速运动了。可见恒定牵引力的加速时功率一定不恒定。这种加速过程发动机做的功只能用W=Fžs计算,不能用W=Pžt计算(因为P为变功率)。
,此后汽车要想继续加速就只能做恒定功率的变加速运动了。可见恒定牵引力的加速时功率一定不恒定。这种加速过程发动机做的功只能用W=Fžs计算,不能用W=Pžt计算(因为P为变功率)。
要注意两种加速运动过程的最大速度的区别。
[例8] 质量为2t的农用汽车,发动机额定功率为30kW,汽车在水平路面行驶时能达到的最大时速为54km/h。若汽车以额定功率从静止开始加速,当其速度达到v=36km/h时的瞬时加速度是多大?
解析:汽车在水平路面行驶达到最大速度时牵引力F等于阻力f,即Pm=fžvm,而速度为v时的牵引力F=Pm/v,再利用F-f=ma,可以求得这时的a=0.50m/s2
[例9]卡车在平直公路上从静止开始加速行驶,经时间t前进距离s,速度达到最大值vm。设此过程中发动机功率恒为P,卡车所受阻力为f,则这段时间内,发动机所做的功为( )
A.Pt B.fs C.Pt=fs D.fvmt
解析:发动机所做的功是指牵引力的功。由于卡车以恒定功率运动,所以发动机所做的功应等于发动机的功率乘以卡车行驶的时间,∴A对。B项给出的是卡车克服阻力做的功,在这段时间内,牵引力的功除了克服阻力做功外还要增加卡车的功能,∴B错。C项给出的是卡车所受外力的总功。D项中,卡车以恒功率前进,将做加速度逐渐减小的加速运动,达到最大速度时牵引力等于阻力,阻力f乘以最大速度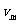 是发动机的功率,再乘以t恰是发动机在t时间内做的功。故A D是正确的。
是发动机的功率,再乘以t恰是发动机在t时间内做的功。故A D是正确的。
[例10]质量为m、额定功率为P的汽车在平直公路上行驶。若汽车行驶时所受阻力大小不变,并以额定功率行驶,汽车最大速度为v1,当汽车以速率v2(v2<v1)行驶时,它的加速度是多少?
解析:速度最大时,牵引力最小,在量值上等于阻力。所以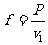 ,以速率v2运动时,由牛顿第二定律有: F-f=ma
,以速率v2运动时,由牛顿第二定律有: F-f=ma
其中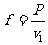 ,
, 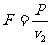
得 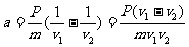
[例11]质量是2000kg、额定功率为80kW的汽车,在平直公路上行驶中的最大速度为20m/s。若汽车从静止开始做匀加速直线运动,加速度大小为2m/s2,运动中的阻力不变。求:①汽车所受阻力的大小。②3s末汽车的瞬时功率。③汽车做匀加速运动的时间。④汽车在匀加速运动中牵引力所做的功。
解析:①所求的是运动中的阻力,若不注意“运动中的阻力不变”,则阻力不易求出。以最大速度行驶时,根据P=Fv,可求得F=4000N。而此时牵引力和阻力大小相等。
②由于3s时的速度v=at=6m/s,而牵引力由F-Ff=ma得F=8000N,故此时的功率为P= Fv =4.8×104W。
③设匀加速运动的时间为t,则t时刻的速度为v=a t=2t,这时汽车的功率为额定功率。由P=Fv,将F=8000N和v=2 t代入得t=5s。
④虽然功率在不断变化,但功率却与速度成正比,故平均功率为额定功率的一半,从而得牵引力的功为W=Pt=40000×5J=2×105J.
点评:③中的时间,有的学生用v=at,得t=vm/a=10s,这是错误的。要注意,汽车不是一直匀加速到最大速度的。
[例12]
质量为0.5kg的物体从高处自由下落,在下落的前2s内重力对物体做的功是多少?这2s内重力对物体做功的平均功率是多少?2s末,重力对物体做功的即时功率是多少?(g取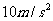 )
)
解析:前2s,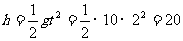 m,
m,
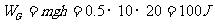 ,
,
平均功率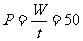 W,
W,
2s末速度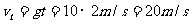 ,
,
2s末即时功率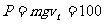 W。
W。
3.一对作用力和反作用力做功的特点
(1)一对作用力和反作用力在同一段时间内,可以都做正功、或者都做负功,或者一个做正功、一个做负功,或者都不做功。
(2)一对作用力和反作用力在同一段时间内做的总功可能为正、可能为负、也可能为零。
(3)一对互为作用反作用的摩擦力做的总功可能为零(静摩擦力)、可能为负(滑动摩擦力),但不可能为正。
点评:一对作用力和反作用力在同一段时间内的冲量一定大小相等,方向相反,矢量和为零。
[例7] 关于力对物体做功,以下说法正确的是( )
A.一对作用力和反作用力在相同时间内做的功一定大小相等,正负相反
B.不论怎样的力对物体做功,都可以用W=Fscosα
C.合外力对物体不作功,物体必定做匀速直线运动
D.滑动摩擦力和静摩擦力都可以对物体做正功或负功
解析:一对作用力和反作用力一定大小相等、方向相反,而相互作用的两物体所发生的位移不一定相等,它们所做的功不一定大小相等,所以,它们所做的功不一定大小相等,正负相反。公式W=Fscosα,只适用于恒力功的计算。合外力不做功,物体可以处于静止。滑动摩擦力、静摩擦力都可以做正功或负功,如:在一加速行驶的卡车上的箱子,若箱子在车上打滑(有相对运动),箱子受滑动摩擦力,此力对箱子做正功;若箱子不打滑(无相对运动),箱子受静摩擦力,对箱子也做正功。故D是正确的。
2.功的物理含义
关于功我们不仅要从定义式W=Fs cos α 进行理解和计算, 还应理解它的物理含义. 功是能量转化的量度,即:做功的过程是能量的一个转化过程,这个过程做了多少功,就有多少能量发生了转化.对物体做正功,物体的能量增加.做了多少正功,物体的能量就增加了多少;对物体做负功,也称物体克服阻力做功,物体的能量减少,做了多少负功,物体的能量就减少多少.因此功的正、负表示能的转化情况,表示物体是输入了能量还是输出了能量.
[例5]质量为m的物体,受水平力F的作用,在粗糙的水平面上运动,下列说法中正确的是( )
A.如果物体做加速直线运动,F一定做正功
B.如果物体做减速直线运动,F一定做负功
C.如果物体做减速直线运动,F可能做正功
D.如果物体做匀速直线运动,F一定做正功
解析:物体在粗糙水平面上运动,它必将受到滑动摩擦力,其方向和物体相对水平面的运动方向相反。当物体做加速运动时,其力F方向必与物体运动方向夹锐角(含方向相同),这样才能使加速度方向与物体运动的方向相同。此时,力F与物体位移的方向夹锐角,所以,力F对物体做正功, A对。
当物体做减速运动时,力F的方向可以与物体的运动方向夹锐角也可以夹钝角(含方向相反),只要物体所受合力与物体运动方向相反即可,可见,物体做减速运动时,力F可能对物体做正功,也可能对物体做负功, B错,C对。
当物体做匀速运动时,力F的方向必与滑动摩擦力的方向相反,即与物体位移方向相同,所以,力F做正功,D对。
故A、C、D是正确的。
[例6]如图所示,均匀长直木板长L=40cm,放在水平桌面上,它的右端与桌边相齐,木板质量m=2kg,与桌面间的摩擦因数μ=0.2,今用水平推力F将其推下桌子,则水平推力至少做功为( )(g取10/s2)
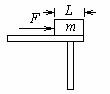
A.0.8J B.1.6J C.8J D.4J
解析:将木板推下桌子即木块的重心要通过桌子边缘,水平推力做的功至少等于克服滑动摩擦力做的功,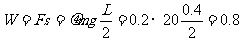 J。故A是正确的。
J。故A是正确的。
1.功
功是力的空间积累效应。它和位移相对应(也和时间相对应)。计算功的方法有两种:
(1)按照定义求功。即:W=Fscosθ。 在高中阶段,这种方法只适用于恒力做功。当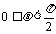 时F做正功,当
时F做正功,当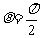 时F不做功,当
时F不做功,当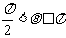 时F做负功。
时F做负功。
这种方法也可以说成是:功等于恒力和沿该恒力方向上的位移的乘积。
(2)用动能定理W=ΔEk或功能关系求功。当F为变力时,高中阶段往往考虑用这种方法求功。这里求得的功是该过程中外力对物体做的总功(或者说是合外力做的功)。
这种方法的依据是:做功的过程就是能量转化的过程,功是能的转化的量度。如果知道某一过程中能量转化的数值,那么也就知道了该过程中对应的功的数值。
 [例1] 如图所示,质量为m的小球用长L的细线悬挂而静止在竖直位置。在下列三种情况下,分别用水平拉力F将小球拉到细线与竖直方向成θ角的位置。在此过程中,拉力F做的功各是多少?
[例1] 如图所示,质量为m的小球用长L的细线悬挂而静止在竖直位置。在下列三种情况下,分别用水平拉力F将小球拉到细线与竖直方向成θ角的位置。在此过程中,拉力F做的功各是多少?
⑴用F缓慢地拉;
⑵F为恒力;
⑶若F为恒力,而且拉到该位置时小球的速度刚好为零。
可供选择的答案有
A.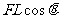 B.
B.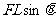 C.
C. D.
D.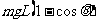
解析:
⑴若用F缓慢地拉,则显然F为变力,只能用动能定理求解。F做的功等于该过程克服重力做的功。选D
⑵若F为恒力,则可以直接按定义求功。选B
⑶若F为恒力,而且拉到该位置时小球的速度刚好为零,那么按定义直接求功和按动能定理求功都是正确的。选B、D
在第三种情况下,由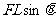 =
=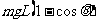 ,可以得到
,可以得到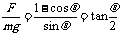 ,可见在摆角为
,可见在摆角为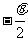 时小球的速度最大。实际上,因为F与mg的合力也是恒力,而绳的拉力始终不做功,所以其效果相当于一个摆,我们可以把这样的装置叫做“歪摆”。
时小球的速度最大。实际上,因为F与mg的合力也是恒力,而绳的拉力始终不做功,所以其效果相当于一个摆,我们可以把这样的装置叫做“歪摆”。
[例2]如图所示,线拴小球在光滑水平面上做匀速圆周运动,圆的半径是1m,球的质量是0.1kg,线速度v=1m/s,小球由A点运动到B点恰好是半个圆周。那么在这段运动中线的拉力做的功是( )
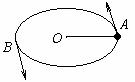
A.0 B.0.1J C.0.314J D.无法确定
解析:小球做匀速圆周运动,线的拉力为小球做圆周运动的向心力,由于它总是与运动方向垂直,所以,这个力不做功。故A是正确的。
[例3]下面列举的哪几种情况下所做的功是零( )
A.卫星做匀速圆周运动,地球引力对卫星做的功
B.平抛运动中,重力对物体做的功
C.举重运动员,扛着杠铃在头上的上方停留10s,运动员对杠铃做的功
D.木块在粗糙水平面上滑动,支持力对木块做的功
解析:引力作为卫星做圆周运动的向心力,向心力与卫星运动速度方向垂直,所以,这个力不做功。杠铃在此时间内位移为零。支持力与位移方向垂直,所以,支持力不做功。故A、C、D是正确的。
[例4]用力将重物竖直提起,先是从静止开始匀加速上升,紧接着匀速上升。如果前后两过程的运动时间相同,不计空气阻力,则( )
A.加速过程中拉力做的功比匀速过程中拉力做的功大
B.匀速过程中拉力做的功比加速过程中拉力做的功大
C.两过程中拉力做的功一样大
D.上述三种情况都有可能
解析:应先分别求出两过程中拉力做的功,再进行比较。重物在竖直方向上仅受两个力作用,重力mg、拉力F。
匀加速提升重物时,设拉力为F1,物体向上的加速度为a,根据牛顿第二定律
得F1-mg=ma
拉力F1所做的功
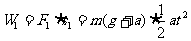
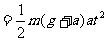 ①
①
匀速提升重物时,设拉力为F2,根据平衡条件得F2=mg
匀速运动的位移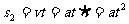
所以匀速提升重物时拉力的功
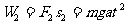 ②
②
比较①、②式知:当a>g时,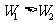 ;当a=g时,
;当a=g时,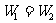 ;当a<g时,
;当a<g时,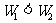
故D选项正确。
点评:可见,力对物体所做的功的多少,只决定于力、位移、力和位移间夹角的大小,而跟物体的运动状态无关。在一定的条件下,物体做匀加速运动时力对物体所做的功,可以大于、等于或小于物体做匀速直线运动时该力的功。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com