
(八)基本初等函数Ⅱ(三角函数)
1.任意角、弧度
了解任意角的概念和弧度制的概念;能进行弧度与角度的互化。
2.三角函数
理解任意角三角函数(正弦、余弦、正切)的定义;能用单位圆中的三角函数线推导出 的正弦、余弦、正切的诱导公式及
的正弦、余弦、正切的诱导公式及 的正弦、余弦的诱导公式;能画出y=sin x, y=cos x, y=tan x的图象,了解三角函数的周期性;理解正弦函数、余弦函数在[0,2π]上的性质(如单调性、最大值和最小值、图象与x轴交点等),理解正切函数在(
的正弦、余弦的诱导公式;能画出y=sin x, y=cos x, y=tan x的图象,了解三角函数的周期性;理解正弦函数、余弦函数在[0,2π]上的性质(如单调性、最大值和最小值、图象与x轴交点等),理解正切函数在(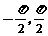 )上的单调性;理解同角三角函数的基本关系式:sin2x+cos2x=1,
)上的单调性;理解同角三角函数的基本关系式:sin2x+cos2x=1,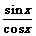 =tan x;了解函数
=tan x;了解函数
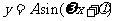 的实际意义,了解函数
的实际意义,了解函数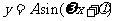 中参数A,
中参数A,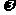 ,
,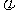 对函数图象变化的影响;会用三角函数解决一些简单实际问题。
对函数图象变化的影响;会用三角函数解决一些简单实际问题。
(七)概率
1. 事件与概率
了解随机事件发生的不确定性和频率的稳定性,了解概率的意义及频率与概率的区别;了解两个互斥事件的概率加法公式。
2.古典概型
理解古典概型及概率计算公式;会计算一些随机事件的基本事件数及其发生的概率。
3.随机数与几何概型
了解随机数的意义,了解几何概型的意义,能运用模拟方法估计概率。
(六)统计
1. 随机抽样
理解随机抽样;会用简单随机抽样方法从总体中抽取样本;了解分层抽样和系统抽样方法。
2. 用样本估计总体
了解分布的意义和作用,能根据频率分布表画频率分布直方图、频率折线图、茎叶图,了解他们各自的特点;理解样本数据标准差的意义和作用,会计算数据标准差(不要求记忆公式);能从样本数据中提取基本的数字特征(如平均数、标准差),并作出合理的解释;会用样本的频率分布估计总体分布,会用样本的基本数字特征估计总体的基本数字特征,理解样本估计总体的思想;会用随机抽样的基本方法和样本估计总体的思想,解决一些简单的实际问题。
3. 变量的相关性
会作两个有关联变量的数据的散点图,并利用散点图认识变量间的相关关系;了解最小二乘法的思想,能根据给出的线性回归方程系数公式建立线性回归方程(线性回归方程系数公式不要求记忆)。
(五)算法初步
1.算法的含义、程序框图
了解算法的含义,了解算法的思想;理解程序框图的三种基本逻辑结构:顺序、条件分支、循环。
2.基本算法语句
了解几种基本算法语句--输入语句、输出语句、赋值语句、条件语句、循环语句的含义。
3.算法案例
了解秦九韶算法、辗转相除法、更相减损术等算法案例。
(四)平面解析几何初步
1.直线与方程
掌握确定直线位置的几何要素;理解直线的倾斜角和斜率的概念,掌握过两点的直线斜率的计算公式;能根据两条直线的斜率判定这两条直线平行或垂直;掌握直线方程的三种形式(点斜式、两点式及一般式),了解斜截式与一次函数的关系;能用解方程组的方法求两相交直线的交点坐标;掌握两点间的距离公式、点到直线的距离公式,会求两平行直线间的距离。
2.圆与方程
掌握确定圆的几何要素,掌握圆的标准方程与一般方程;能根据给定直线、圆的方程,判断直线与圆的位置关系;能根据给定两个圆的方程判断圆与圆的位置关系;能用直线和圆的方程解决一些简单的问题;了解用代数方法处理几何问题的思想。
3.空间直角坐标系
了解空间直角坐标系,会用空间直角坐标刻画点的位置;会求空间两点间的距离。
(三)立体几何初步
1.空间几何体
了解柱、锥、台、球及其简单组合体的结构特征,会用这些特征描述现实生活中简单物体的结构;能画出简单空间图形(长方体、球、圆柱、圆锥、棱柱等的简易组合)的三视图,能识别上述的三视图所表示的立体模型,会用斜二侧法画出它们的直观图;会用平行投影方法画出简单空间图形的三图视与直观图,了解空间图形的不同表示形式;了解球、棱柱、棱锥、台的表面积和体积的计算公式(不要求记忆公式)。
2. 点、直线、平面之间的位置关系
理解空间直线、平面位置关系的定义,会用以下公理和定理进行推理:
◆公理1:如果一条直线上的两点在一个平面内,那么这条直线在此平面内。
◆公理2:过不在一条直线上的三点,有且只有一个平面。
◆公理3:如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线。
◆公理4:平行于同一条直线的两条直线平行。
◆定理:空间中如果两个角的两条边分别对应平行,那么这两个角相等或互补。
以立体几何的上述定义、公理和定理为出发点,通过直观感知、操作确认、思辨论证,认识和理解空间中线面平行、垂直的有关性质与判定。
理解以下判定定理并用以证明一些空间位置关系的简单命题:
◆平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行。
◆一个平面内的两条相交直线与另一个平面平行,则这两个平面平行。
◆一条直线与一个平面内的两条相交直线垂直,则该直线与此平面垂直。
◆ 一个平面过另一个平面的垂线,则两个平面垂直。
掌握以下性质定理并用以证明一些空间位置关系的简单命题:
◆一条直线与一个平面平行,则过该直线的任一个平面与此平面的交线与该直线平行。
◆两个平面平行,则任意一个平面与这两个平面相交所得的交线相互平行。
◆垂直于同一个平面的两条直线平行。
◆两个平面垂直,则一个平面内垂直于交线的直线与另一个平面垂直。
(二)函数概念与基本初等函数Ⅰ
1.函数
了解构成函数的要素,会求一些简单函数的定义域和值域,了解映射的概念;会根据不同的需要选择恰当的方法(如图象法、列表法、解析法)表示函数;了解简单的分段函数,并能简单应用(函数分段不超过三段);理解函数的单调性、最大(小)值及其几何意义;了解函数奇偶性的含义;会运用基本初等函数的图象分析函数的性质。
2.指数函数
理解有理指数幂的含义,了解实数指数幂的意义,掌握有理指数幂的运算及性质;理解指数函数的概念及其单调性,掌握函数图象通过的特殊点,会画底数为2、3、10、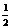 、
、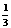 的指数函数的图象;知道指数函数是一类重要的函数模型。
的指数函数的图象;知道指数函数是一类重要的函数模型。
3. 对数函数
理解对数的概念及其运算性质,会用换底公式将一般对数转化成自然对数或常用对数,了解对数在简化运算中的作用;理解对数函数的概念及其单调性,掌握对数函数图象通过的特殊点,会画底数为2、10、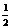 的对数函数的图象;知道对数函数是一类重要的函数模型,知道指数函数
的对数函数的图象;知道对数函数是一类重要的函数模型,知道指数函数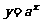 (a > 0,且
a≠1) 与对数函数
(a > 0,且
a≠1) 与对数函数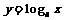 (a > 0, a≠1)互为反函数。
4. 幂函数
(a > 0, a≠1)互为反函数。
4. 幂函数
了解幂函数的概念;了解幂函数y=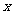 ,y=
,y=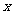 2,y=
2,y=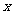 3,
3,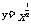 ,
,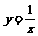 的图象的变化情况。
的图象的变化情况。
5.函数与方程
了解函数的零点与方程根的联系,会判断一元二次方程根的存在性与根的个数;会用二分法求相应方程的近似解。
6.函数模型及其应用
了解指数函数、对数函数、幂函数的增长特征,知道直线上升、指数爆炸、对数增长等不同函数类型增长的含义;了解函数模型(如指数函数、对数函数、幂函数、分段函数等在社会生活中普遍使用的函数模型)的广泛应用。
(一)集合
1.集合的含义与表示
了解集合的含义,了解元素与集合的关系;能用自然语言、图形语言、集合语言(列举法或描述法)描述具体问题。
2.集合间的基本关系
理解集合之间包含与相等的含义;了解全集、子集、空集的含义。
3.集合的基本运算
理解两个集合的并集与交集的含义,会求两个简单集合的并集与交集;理解补集的含义,会求给定子集的补集;会用Venn图表达两个简单集合间的关系及运算。
普通高中《数学课程标准》所规定的五个必修模块的学习内容。具体分述如下:
4.个性品质
个性品质是指学生个体的情感、态度和价值观。要求学生具有一定的数学视野,认识数学的科学价值和人文价值,崇尚数学的理性精神,形成审慎思维的习惯,体会数学的美学意义。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com