21．(本小题满分14分)

设A(X₁,Y₁),B(X₂,Y₂)是平面直角坐标系xOy上的两点，先定义由点A到点B的一种折线距离p(A,B)为

对于平面xOy上给定的不同的两点AA(X₁,Y₁),B(X₂,Y₂)

(1)　　 若点C(x, y)是平面xOy上的点，试证明

(2)　　 在平面xOy上是否存在点c(x, y),同时满足

20．(本小题满分为14分)

　一直双曲线 　　的左、右顶点分别为A₁,A₂，点P(X₁,Y₁)，Q(X₁,-Y₁)是双曲线上不同的两个动点

(1)　　　 求直线A与A₂Q交点的轨迹E的方程式；

(2)　　　 若点H(O, h)(h>1)的两条直线l₁和l₂与轨迹E都只有一个交点，且l_{1　 　,}求h的值。

19.(本小题满分12分)

　 某营养师要为某个儿童预定午餐和晚餐，已知一个单位的午餐含12个单位的碳水化合物6个单位蛋白质和6个单位的维生素C；一个单位的晚餐含8个单位的碳水化合物，6个单位的蛋白质和10个单位的维生素C.另外，该儿童这两餐需要的营养中至少含64个单位的

碳水化合物，42各单位的蛋白质和54个单位的维生素C.

　 如果一个单位的午餐、晚餐的费用分别是2.5元和4元，那么要满足上述的营养要求，并且花费最少，应当为该儿童分别预定多少个单位的午餐和晚餐？

18.(本小题满分14分)

如图5⌒AEC是半径为a的半圆，AC为直径，点E为⌒AC的中点，点B和点C为线段图图5

AD的三等分点。平面AEC外一点F满足FB=FD=√　5a，FE=√　6a

(1)　　　 证明：EB⊥FD

(2)已知点Q,R分别为线段FE,FB上的点，使得BQ=FE,FR=FB,求平面BED与平面RQD所成二面角的正弦值。

17.(本小题满分12分)

某食品厂为了检查一条自动包装流水线的生产情况，随即抽取该流水线上40件产品作为样本算出他们的重量(单位：克)重量的分组区间为(490,495)，(495,500)，。。。(510,515)，

由此得到样本的频率分布直方图，

如图4所示。

(1)　　　 根据频率分布直方图，求重量超过505

克的产品总量。

(2)　　　 在上述抽取的40件产品中任取2件，设

Y为重量超过505克的产品数量，求Y的分布列。

(3)　　　 从流水线上任取5件产品，求恰有2件产

(4)　　　 品合格的重量超过505克的概率。

16、(本小题满分14分)　

(1)　　 求f(x)的最小正周期；

(2)　　 求f(x)的解析式；

(3)　　 若f(2/3α　+PI /12)=12/5,求sinα　

(一)必做题(9-13)

9.函数f(x)=lg(x-2)的定义域是　　　　　 。

10.若向量a=(1,1,x),b=(1,2,1),c=(1,1,1),满足条件(，a)·(2b)=-2,则x=　　　　 .

11.已知a,b,c分别是△ABC的三个内角A,B,C所对的边，若a=1,b=√3,A+B=2B,则sinC=　　 .

12.已知圆心在x轴上，半径为√2的圆O位于y轴左侧，且与直线x+y=0相切，则圆O的方程是　　　 。

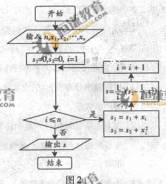
13.某城市缺水问题比较突出，为了制定节水管理办法，对全市居民某年的月均用水量进行了抽样调查，其中n位居民的月均用水量分别为x₁…x_n(单位：吨)，根据图2所示的程序框图，若n=2,且x_1，x₂ 分别为1,2，则输出地结果s为　　 。

(二)选做题(14-15题，考生只能从中选做一题)

14、(几何证明选讲选做题)如图3，AB，CD是半径为a的圆O的两条弦，它们相交于AB的中点P，PD=2a/3，∠OAP=30　^o，则CP＝______.

15、(坐标系与参数方程选做题)在极坐标系(ρ，θ)(0　≤　θ<2π)中，曲线ρ= 与的交点的极坐标为______。

8.为了迎接2010年广州亚运会，某大楼安装5个彩灯，他们闪亮的顺序不固定，每个彩灯彩灯闪亮只能是红橙黄绿蓝中的一种颜色，切这5个彩灯商量的颜色各不相同，记得这5个彩灯有序地闪亮一次为一个闪烁，而相邻两个闪烁的时间间隔均为5妙。在每一个闪烁中，那没需要的时间至少是

A1205秒　　　　　 B1200秒　　　 C1195秒　　　　 D1190秒

6.如图1.为三角形，AA^’‖BB^’　‖CC^’　, CC⊥平面ABC　且3AA^’=BB^’=cc^’ =AB,则多面体ABC-A^‘B^’C^‘

的正视图是

ABCD

7已知随机变量X服从整台分布N(3.1)，且p(2　≤X　≤4)=0.6826.则p(X>4)=。

A　 0.1588　　　　　 　B　 0.1587　　　 　C　 0.1586　　　　　 　D　 0.1585

5. “”是“一元二次方程x2+x+m=0”有实数解“的

A．充分非必要条件　　　　　　　　 B.充分必要条件

C．必要非充分条件　　　　 　　　　D.非充分必要条件