2．随着医疗技术的进步和医疗条件的改善，传染性疾病逐渐得到了控制，而遗传病已成为威胁人类健康的一个重要因素，下面对遗传病的认识正确的一项是

　　 A．成年后才患有的疾病不是遗传病，而出生时就患有的疾病则是遗传病

　　 B．一个家族仅在一代人中出现过的疾病不是遗传病，一个家族在几代人中都出现过的疾病是遗传病

　　 C．研究某遗传病的发病率，一般要选择多个有此病的家族进行研究统计计算发病率

　　 D．苯丙酮尿症是一种单基因遗传病，致病基因位于常染色体上，可通过尿液化验来诊断

1．将物质的量浓度都相同的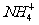、、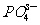K⁺、Ca²⁺共同置于500 mL水中，再放入一些生长旺盛的水稻幼苗，一天之后发现溶液的体积是400mL，，再测定溶液中上述四种离子含量变化如下：

项目		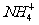、K+	Ca2+
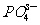变化后浓度	83%	72%	98%	122%

　　 下面是通过该实验得到的结论，其中错误的是

A．水稻幼苗对水分的吸收和对矿质离子的吸收是两个相对独立的过程

　　 B．根对四种离子的吸收量有差异，说明根对离子的吸收具有选择性

　　 C．根对矿质离子的吸收需要消耗能量

　　 D．水稻对K⁺的吸收速度快于其他三种离子

22．(本小题满分12分)

　　 已知函数f(x)＝lnax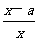－(a≠0)．

　 (Ⅰ)求此函数的单调区间及最值；

　 (Ⅱ)求证：对于任意正整数n，均有1+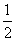++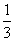…+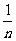≥ln ；

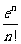　 (Ⅲ)当a＝1时，是否存在过点(1，－1)的直线与函数y＝f(x)的图象相切?若存在，有多少条?若不存在，说明理由．

21．(本小题满分12分)

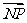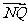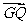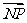　　 已知圆M：(x－m)²+(y－n)²＝γ²及定点N(1，0)，点P是圆M上的动点，点Q在NP上，点G在MP上，且满足＝2，·＝0．

　 (Ⅰ)若m＝－1，n＝0，r＝4，求点G的轨迹C的方程；

　 (Ⅱ)若动圆M和(Ⅰ)中所求轨迹C相交于不同两点A、B，是否存在一组正实数m，n，r使得直线MN垂直平分线段AB，若存在，求出这组正实数；若不存在，说明理由．

20．(本小题满分12分)

　　 某中学举办“上海世博会”知识宣传活动，现场的“抽卡有奖游戏”特别引人注目，游戏规则是：盒子中装有8张形状大小相同的精美卡片，卡片上分别印有“世博会吉祥物海宝”或“世博会会徽”，要求4人一组参加游戏，参加游戏的4人从盒子中轮流抽取卡片，一次抽2张，抽取后不放回，直到4人中某人一次抽到2张“世博会吉祥物海宝”卡才能获奖，当某人获奖或者盒中卡片抽完时游戏终止．

　 (Ⅰ)游戏开始之前，一位高中生问：“盒子中有几张‘世博会会徽’卡?”主持人说：“若从盒中任抽2张卡片不都是‘世博会会徽’卡的概率为”请你回答有几张“世博会会徽”卡呢?

　 (Ⅱ)在(Ⅰ)的条件下，甲、乙、丙、丁4人参加游戏，约定甲、乙、丙、丁依次抽取．用随机变量ξ表示游戏终止时总共抽取的次数(注意，一次抽取的是两张卡片)，求ξ的分布列和数学期望．

19．(本小题满分12分)

已知函数f(x)＝2x+1，g(x)＝x，x∈R，数列{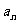}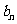，{}满足条件：a₁＝1，＝

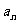f(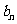)＝g(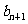)，n∈N﹡．

　 (Ⅰ)求证：数列{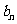+1}为等比数列；

　 (Ⅱ)令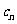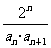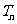＝，是数列{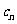}的前n项和，求使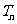>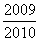成立的最小的n值.

18．(本小题满分12分)

　　 如图1，在直角梯形ABCD中，AB∥CD，∠BAD＝90°，AB＝2，AD＝3，CD＝1，点E、F分别在AD、BC上，且AE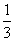＝AD,BF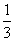＝BC．现将此梯形沿EF折至使AD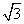＝的位置(如图2)．

(Ⅰ)求证：AE⊥平面ABCD；

　 (Ⅱ)求点B到平面CDEF的距离；　　

　 (Ⅲ)求直线CE与平面BCF所成角的正弦值．

17．(本小题满分10分)

在△ABC中，a、b、c分别是角A、B、C的对边，m＝(2b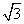－c，cosC)，n＝

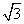(a，cosA)，且m∥n．

(Ⅰ)求角A的大小；

　 (Ⅱ)求2cos ²B+sin(A－2B)的最小值．

16．已知函数y＝f(x)是R上的偶函数，对于x∈R都有f(x－6)＝f(x)+f(3)成立，且f(0)＝－2，当x₁，x₂∈[0，3]，且x₁≠x₂时，都有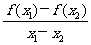>0．则给出下列命题：

①f(2010)＝－2；②函数y＝f(x)图象的一条对称轴为x＝－6；③函数y＝f(x)在[－9，－6]上为增函数；④方程f(x)＝0在[－9，9]上有4个根．其中所有正确命题的序号是__________.

15．设正数x，y满足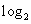(x+y+3)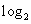＝x+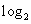y，则x+y的取值范围是__________．