
第一节 听力理解(共15小题;每小题2分,满分30分)
每段播放两遍。各段后有几个小题,各段播放前每小题有5秒钟的阅题时间。请根据各段播放内容及其相关小题,在5秒钟内从题中所给的A、B、C项中,选出最佳选项,并在答题卡上将该项涂黑。
听下面一段对话,回答第1-3三个小题。
1. Where will the girl and her father be at 2:45p.m.?
A. At the meeting room.
B. At the cinema.
C. In the restaurant.
2. Why does the father want to go to the beach?
A. There are many people on the beach.
B. The daughter doesn’t like walking in the park.
C. The mommy likes fresh air on the beach.
3. What food will the family have this evening?
A. Japanese food. B. Chinese food. C. Western food.
听下面一段对话,回答第4-6三个小题。
4. Why does Lisa come back from Hong Kong?
A. She misses home.
B. She’s having a holiday.
C. She doesn’t like Hong Kong.
5. What is important at Easter?
A. Baskets B. Candies C. Eggs
6. What is the relationship between the boy and the girl?
A. Brother and sister B. Neighbors C. Teacher and student
听下面一段对话,回答第7-9三个小题。
7. Who is the man talking to?
A. A sports official. B. A driver. C. A shop assistant.
8. Which of the following shows the right way to the Center?
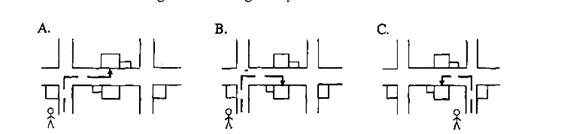
9. What did the man do at last to help himself find the place?
A. Call a taxi. B. Buy a city map. C. Phone his friends.
听下面一段独白,回答第10-12三个小题。
10. Where does the talk take place?
A. In Yunnan B. In the classroom C. On the playground
11. What is the first announcement about?
A. Giving help to people in southwest of China.
B. Miss Liu’s class.
C. Getting news from newspaper.
12. What will children do in Miss Liu’s English class tomorrow?
A. Visit Miss Liu because she’s ill.
B. Play outside.
C. Share reading.
听下面一段独白,回答第13-15三个小题。
13. What does the man talk about on the radio?
A. Earth Hour B. Australia C. How to turn off the lights
14. How long has Earth Hour been held?
A. Seven years B. One year C. Three years
15. What shouldn’t people do in their daily life according to the talk?
A. Turn off the water tap.
B. Use plastic bags as often as possible.
C. Cook at home.
(17)(本小题满分10分)(注意:在试题卷上作答无效)
已知 的内角
的内角 ,
, 及其对边
及其对边
 ,
,
 满足
满足 ,求内角
,求内角 .
.
(18)(本小题满分12分)(注意:在试题卷上作答无效)
投到某杂志的稿件,先由两位初审专家进行评审.若能通过两位初审专家的评审,
则予以录用;若两位初审专家都未予通过,则不予录用;若恰能通过一位初审专家的评
审,则再由第三位专家进行复审,若能通过复审专家的评审,则予以录用,否则不予录
用.设稿件能通过各初审专家评审的概率均为0.5,复审的稿件能通过评审的概率为0.3.
各专家独立评审.
(I)求投到该杂志的1篇稿件被录用的概率;
(II)记 表示投到该杂志的4篇稿件中被录用的篇数,求
表示投到该杂志的4篇稿件中被录用的篇数,求 的分布列及期望.
的分布列及期望.
(19)(本小题满分12分)(注意:在试题卷上作答无效)
如图,四棱锥S-ABCD中,SD 底面ABCD,AB//DC,AD
底面ABCD,AB//DC,AD DC,AB=AD=1,DC=SD=2,E为棱SB上的一点,平面EDC
DC,AB=AD=1,DC=SD=2,E为棱SB上的一点,平面EDC 平面SBC .
平面SBC .
(Ⅰ)证明:SE=2EB;
 (Ⅱ)求二面角A-DE-C的大小 .
(Ⅱ)求二面角A-DE-C的大小 .
(20 )(本小题满分12分)(注意:在试题卷上作答无效)
)(本小题满分12分)(注意:在试题卷上作答无效)
已知函数 .
.
(Ⅰ)若 ,求
,求 的取值范围;
的取值范围;
(Ⅱ)证明: .
.
(21)(本小题满分12分)(注意:在试题卷上作答无效)
已知抛物线 的焦点为F,过点
的焦点为F,过点 的直线
的直线 与
与 相交于
相交于 、
、 两点,点A关于
两点,点A关于 轴的对称点为D .
轴的对称点为D .
(Ⅰ )证明:点F在直线BD上;
)证明:点F在直线BD上;
( Ⅱ)设
Ⅱ)设 ,求
,求 的内切圆M的方程 .
的内切圆M的方程 .
(22)(本小题满分12分)(注意:在试题卷上作答无效)
已知数列 中,
中,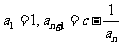 .
.
(Ⅰ)设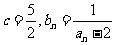 ,求数列
,求数列 的通项公式;
的通项公式;
(Ⅱ)求使不等式 成立的
成立的 的取值范围 .
的取值范围 .
(注意:在试题卷上作答无效 )
)
(13)不等式 的解集是
.
的解集是
.
(14)已知 为第三象限的角,
为第三象限的角, ,则
,则 .
.
(15)直线 与曲线
与曲线 有四个交点,则
有四个交点,则 的取值范围是 .
的取值范围是 .
(16)已知 是椭圆
是椭圆 的一个焦点,
的一个焦点, 是短轴的一个端点,线段
是短轴的一个端点,线段 的延长线交
的延长线交 于点
于点 ,
,
且 ,则
,则 的离心率为
.
的离心率为
.
3。第Ⅱ卷共l0小题,共90分。
(1)复数
(A) (B)
(B) (C)12-13
(C)12-13 (D) 12+13
(D) 12+13
(2)记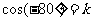 ,那么
,那么
A. B. -
B. - C.
C.  D. -
D. -
(3)若变量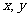 满足约束条件
满足约束条件 则
则 的最大值为
的最大值为
(A)4 (B)3 (C)2 (D)1
(4)已知各项均为正数的等比数列{ },
}, =5,
=5, =10,则
=10,则
 =
=
 (A)
(A)
 (B) 7 (C) 6 (D)
(B) 7 (C) 6 (D) 
(5) 的展开式中x的系数是
的展开式中x的系数是
(A) -4 (B) -2 (C) 2 (D) 4
(6)某校开设A类选修课3门,B类选择课4门,一位同学从中共选3门,若要求两类课程中各至少选一 门,则不同的选法共有
门,则不同的选法共有
(A) 30种 (B)35种 (C)42种 (D)48种
(7)正方体ABCD- 中,B
中,B 与平面AC
与平面AC 所成角的余弦值为
所成角的余弦值为
A  B
B C
C D
D
(8)设a= 2,b=In2,c=
2,b=In2,c= ,则
,则
A a<b<c Bb<c<a C c<a<b D c<b<a
( 9)已知
9)已知 、
、
 为双曲线C:
为双曲线C: 的左、右焦点,点p
的左、右焦点,点p 在C上,∠
在C上,∠ p
p =
= ,则P到x轴的距离为
,则P到x轴的距离为
(A)  (B)
(B) (C)
(C) 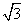 (D)
(D) 
(10)已知函数F(x)=|lgx|,若0<a<b,且f(a)=f(b),则a+2b的取值范围是
(A) (B)
(B) (C)
(C) (D)
(D)
(11)已知圆O的半径为1,PA、PB为该圆的两条切线,A、B为俩切点,那么 的最小值为
的最小值为
 (A)
(A)
 (B)
(B) (C)
(C)  (D)
(D)
(12)已知在半径为2的球面上有A、B、C、D四点,若AB=CD=2,则四面体ABCD的体积的最大值为
(A) 
 (B)
(B) (C)
(C)  (D)
(D) 
第Ⅱ卷
证号填写清楚,然后贴好条形码。请 认真核准条形码上的准考证号、姓名和科目。
认真核准条形码上的准考证号、姓名和科目。
2.第Ⅱ卷共2页,请用直径0.5毫米黑色墨水签字笔在答题卡上各题的答题区域
内作答,在试题卷上作答无效。
23、(10分)已知△ABC的三边长为有理数
(1)求证cosA是有理数
(2)对任意正整数n,求证cosnA也是有理数

22、(10分)某厂生产甲、乙两种产品,生产甲产品一等品80%,二等品20%;生产乙产品,一等品90%,二等品10%。生产一件甲产品,如果是一等品可获利4万元,若是二等品则要亏损1万元;生产一件乙产品,如果是一等品可获利6万元,若是二等品则要亏损2万元。设生产各种产品相互独立
(1)记x(单位:万元)为生产1件甲产品和件乙产品可获得的总利润,求x的分布列
(2)求生产4件甲产品所获得的利润不少于10万元的概率
20.(16分)设 使定义在区间
使定义在区间 上的函数,其导函数为
上的函数,其导函数为 .如果存在实数
.如果存在实数 和函数
和函数 ,其中
,其中 对任意的
对任意的 都有
都有 >0,使得
>0,使得 ,则称函数
,则称函数 具有性质
具有性质 .
.
(1)设函数
 ,其中
,其中 为实数
为实数
①求证:函数 具有性质
具有性质
②求函数 的单调区间
的单调区间
(2)已知函数 具有性质
具有性质 ,给定
,给定
 ,
, ,且
,且 ,若|
,若| |<|
|<| |,求
|,求 的取值范围
的取值范围
[理科附加题]
21(从以下四个题中任选两个作答,每题10分)
(1)几何证明选讲
AB是⊙O的直径,D为⊙O上一点,过点D作⊙O的切线交AB延长线于C,若DA=DC,求证AB=2BC

(2)矩阵与变换
在平面直角坐标系xOy中,A(0,0),B(-3,),C(-2,1),设k≠0,k∈R,M= ,N=
,N= ,点A、B、C在矩阵MN对应的变换下得到点A1,B1,C1,△A1B1C1的面积是△ABC面积的2倍,求实数k的值
,点A、B、C在矩阵MN对应的变换下得到点A1,B1,C1,△A1B1C1的面积是△ABC面积的2倍,求实数k的值
(3)参数方程与极坐标
在极坐标系中,圆ρ=2cosθ与直线3ρcosθ+4ρsinθ+a=0相切,求实数a的值
(4)不等式证明选讲
已知实数a,b≥0,求证:
19.(16分)设各项均为正数的数列 的前n项和为
的前n项和为 ,已知
,已知 ,数列
,数列 是公差为
是公差为 的等差数列.
的等差数列.
①求数列 的通项公式(用
的通项公式(用 表示)
表示)
②设 为实数,对满足
为实数,对满足 的任意正整数
的任意正整数 ,不等式
,不等式 都成立。求证:
都成立。求证: 的最大值为
的最大值为
18. (16分)在平面直角坐标系
(16分)在平面直角坐标系 中,如图,已知椭圆
中,如图,已知椭圆 的左右顶点为A,B,右顶点为F,设过点T(
的左右顶点为A,B,右顶点为F,设过点T( )的直线TA,TB与椭圆分别交于点M
)的直线TA,TB与椭圆分别交于点M ,
, ,其中m>0,
,其中m>0,
①设动点P满足 ,求点P的轨迹
,求点P的轨迹
②设 ,求点T的坐标
,求点T的坐标
③设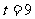 ,求证:直线MN必过x轴上的一定点
,求证:直线MN必过x轴上的一定点
(其坐标与m无关)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com