
2、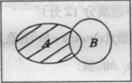 设集合
设集合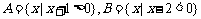 .
.
则右图中阴影部分表示的集合为( )]
A.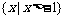 B.
B.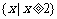
C.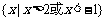 D.
D.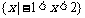
只有一项是符合题目要求的。)
1、设复数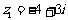 ,
,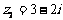 ,则复数
,则复数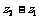 在复平面内对应的点位于( )
在复平面内对应的点位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
22.(本小题满分12分)已知椭圆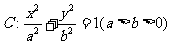 的离心率为
的离心率为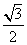 ,过焦点且垂直于长轴的直线被椭圆截得的弦长为
,过焦点且垂直于长轴的直线被椭圆截得的弦长为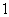 ,过点
,过点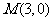 的直线
的直线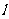 与椭圆
与椭圆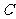 相交于两点
相交于两点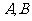 .
.
(1)求椭圆的方程;
(2)设 为椭圆上一点,且满足
为椭圆上一点,且满足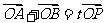 (
(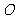 为坐标原点),当
为坐标原点),当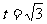 时,求直线
时,求直线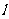 的方程.
的方程.
20.(本小题满分12分)已知数列{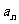 }满足条件:a1=1,
}满足条件:a1=1,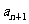 =2
=2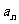 +1,n∈N﹡.
+1,n∈N﹡.
(1)求数列{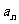 }的通项公式;
}的通项公式;
(2)令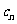 =
=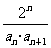 ,
, 是数列{
是数列{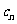 }的前n项和,证明
}的前n项和,证明  <1.
<1.
21(本小题满分12分)已知函数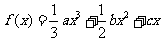 .
.
(1)若函数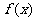 有三个零点
有三个零点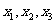 ,且
,且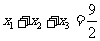 ,
, ,求函数
,求函数 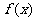 的单调区间;
的单调区间;
(2)在(1)的条件下,若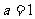 时,函数
时,函数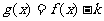 在区间
在区间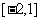 上有两个零点,求
上有两个零点,求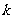 的取值范围.
的取值范围.

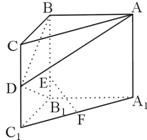
19.(本小题满分12分)如图,在直三棱柱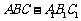 中,
中,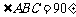 ,
,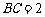 ,
,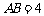 ,
,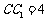 ,E在
,E在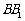 上,且
上,且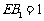 ,
,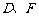 分别为
分别为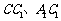 的中点.
的中点.
(1)求证: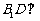 平面
平面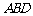 ;
;
(2)求异面直线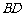 与
与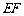 所成的角;
所成的角;
(3)求点 到平面
到平面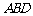 的距离.
的距离.
18. (本小题满分12分)某单位举办2010年上海世博会知识宣传活动,进行现场抽奖.盒中装有9张大小相同的精美卡片,卡片上分别印有“世博会会徽”或“海宝”(世博会吉祥物)图案;抽奖规则是:参加者从盒中抽取卡片两张,若抽到两张都是“海宝”卡即可获奖,否则,均为不获奖.卡片用后放回盒子,下一位参加者继续重复进行.
(1)活动开始后,一位参加者问:盒中有几张“海宝”卡?主持人答:我只知道,从盒中抽取两张都是“世博会会徽”卡的概率是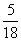 ,求抽奖者获奖的概率;
,求抽奖者获奖的概率;
(2)现有甲、乙、丙、丁四人依次抽奖,求三个人获奖的概率是多少?.
17.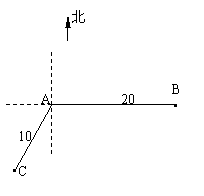 (本题满分10分)如图,当甲船位于A处时获悉,在其正东方向相距20海里的B处有一艘渔船遇险等待营救.甲船立即前往救援,同时把消息告知在甲船的南偏西30
(本题满分10分)如图,当甲船位于A处时获悉,在其正东方向相距20海里的B处有一艘渔船遇险等待营救.甲船立即前往救援,同时把消息告知在甲船的南偏西30 ,相距10海里C处的乙船.
,相距10海里C处的乙船.
(1)求处于C处的乙船和遇险渔船间的距离;
(2)设乙船沿直线 方向前往
方向前往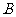 处救援,其方向与
处救援,其方向与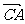 成
成 角,
角,
求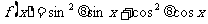 (x∈
(x∈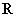 )的值域.
)的值域.
16.给出以下四个结论:
①函数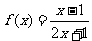 的对称中心是
的对称中心是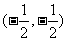 ;
;
②已知向量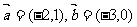 ,则
,则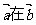 方向上的投影为2;
方向上的投影为2;
③已知点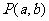 与点
与点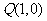 在直线
在直线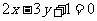 两侧,当
两侧,当
 且
且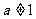 ,
,
 时,
时,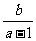 的取值范围为
的取值范围为 ;
;
④若将函数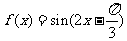 的图像向右平移
的图像向右平移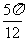 个单位后变为偶函数;
个单位后变为偶函数;
其中正确的结论是:
15.已知函数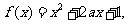 其中
其中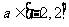 ,则函数
,则函数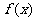 有零点的概率是
有零点的概率是
14.今有2个红球、3个黄球、4个白球,同色球不加以区分,将这9个球排成一列
有 种不同的方法。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com