
2.计算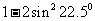 的结果等于
的结果等于
A. B.
B. C.
C.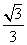 D.
D.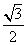
1.若集合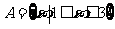 ,
,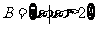 ,则
,则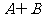 等于
等于
A.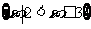 B.
B.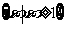 C.
C.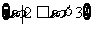 D.
D.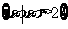
21.(本 小题满分13分)
小题满分13分)
已知函数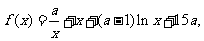 其中a<0,且a≠-1.
其中a<0,且a≠-1.
(Ⅰ)讨论函数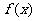 的单调性;
的单调性;
(Ⅱ)设函数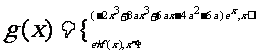 (e是自然数的底数)。是否存在a,使
(e是自然数的底数)。是否存在a,使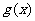 在[a,-a]上为减函数?若存在,求a的取值范围;若不存在
在[a,-a]上为减函数?若存在,求a的取值范围;若不存在 ,请说明理由。
,请说明理由。
20.(本小题满分13分)
给出下面的数表序列:

其中表n(n =1,2,3
=1,2,3  )有n行,第1行的n个数是1,3,5,
)有n行,第1行的n个数是1,3,5, 2n-1,从第2行起,每行中的每个数都等于它肩上的两数之和。
2n-1,从第2行起,每行中的每个数都等于它肩上的两数之和。
(I)写出表4,验证表4各行中数的平均数按从上到下的顺序构成等比数列,并将结论推广到表n(n≥3)(不要求证明);
(II)每个数列中最后一行都只有一个数,它们构成数列1,4,12 ,记此数列为
,记此数列为
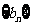 求和:
求和: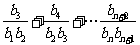
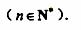
19.(本小题满分13分)
为了考察冰川的融化状况,一支科考队在某冰川山上相距8Km的A、B两点各建一个考察基地,视冰川面为平面形,以过A、B两点的直线为x轴 ,线段AB的垂直平分线为y轴建立平面直角坐标系(图4)。考察范围到A、B两点的距离之和不超过10Km的区域。
,线段AB的垂直平分线为y轴建立平面直角坐标系(图4)。考察范围到A、B两点的距离之和不超过10Km的区域。
(I) 求考察区域边界曲线的方程:
(II)
如图4所示,设线段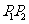 是冰川的部分边界线(不考虑其他边界),当冰川融化时,边界线沿与其垂直的方向朝考察区域平行移动,第一年移动0.2km,以后每年移动的距离为前一年的2倍。问:经过多长时间,点A恰好在冰川边界线上?
是冰川的部分边界线(不考虑其他边界),当冰川融化时,边界线沿与其垂直的方向朝考察区域平行移动,第一年移动0.2km,以后每年移动的距离为前一年的2倍。问:经过多长时间,点A恰好在冰川边界线上?
18.(本小题满分12分)
如图所示,在长方体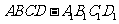 中,AB=AD=1,AA1=2,M是棱CC1的中点
中,AB=AD=1,AA1=2,M是棱CC1的中点
(Ⅰ)求异面直线A1M和C1D1所成的角的正切值;
(Ⅱ)证明:平面ABM⊥平面A1B1M1
17. (本小题满分12分)
为了对某课题进行研究,用 分层抽样方法从三所高校A,B,C的相关人员中,抽取若干人组成研究小组、有关数据见下表(单位:人)
分层抽样方法从三所高校A,B,C的相关人员中,抽取若干人组成研究小组、有关数据见下表(单位:人)
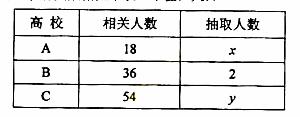
(I) 求x,y ;
(II)
若从高校B、C抽取的人 中选2人作专题发言,求这二人都来自高校C的概率。
中选2人作专题发言,求这二人都来自高校C的概率。
16. (本小题满分12分)
已知函数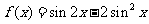
(I)求函数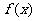 的最小正周期。
的最小正周期。
(II) 求函数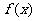 的最大值及
的最大值及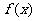 取最大值时x的集合。
取最大值时x的集合。
15.若规定 E=
E=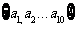 的子集
的子集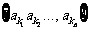 为E的第k个子集,其中k=
为E的第k个子集,其中k= ,则
,则
(1)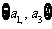 是E的第____个子集;
是E的第____个子集;
(2)E的第211个子集是_______
14.若不同两点P,Q的坐标分别为(a,b),(3-b,3-a),则线段PQ的垂直平分线l的斜率为
,圆(x-2)2+(y-3)2=1关于直线对称的圆的方程为 。[来源:]
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com