22. --May I speak to Professor White, please?

　　 --Sorry, he isn’t in. This is his assistant speaking. Can I help you?

　　 A. Oh, you can　　　　　　　　　　　 B. Oh, it’s a pity

　　 C. I hope to see him soon　　　　　　　 D. I should think so

第一节　 单项填空(共15小题；每小题1分，满分15分)

　　 从A、B、C、D四个选项中，选出可以填入空白处的最佳选项，并在答题卡上将该项涂黑。

21. Obama, ________ president of the USA, won ________ Nobel Prize for Peace in 2009.

A. 不填；a　　　 B. 不填；the　　　 C. a；the　　　　　 D. the；a

22．(本小题满分12分)

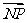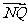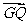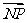　　 已知圆M：(x－m)²+(y－n)²＝γ²及定点N(1，0)，点P是圆M上的动点，点Q在NP上，点G在MP上，且满足＝2，·＝0．

　 (Ⅰ)若m＝－1，n＝0，r＝4，求点G的轨迹C的方程；

　 (Ⅱ)若动圆M和(Ⅰ)中所求轨迹C相交于不同两点A、B，是否存在一组正实数m，n，r使得直线MN垂直平分线段AB，若存在，求出这组正实数；若不存在，说明理由．

21．(本小题满分12分)

　　 已知函数f(x)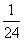＝ax³－bx²+(2－b)x+1(x>0)在x＝x₁和x＝x₂处取得极值，

且0<x₁<1<x₂<2．

　 (Ⅰ)若a，b均为正整数，求函数f(x)的单调增区间；

　 (Ⅱ)若z＝a－12b，求z的取值范围．

20．(本小题满分12分)

　　 某中学举办“上海世博会”知识宣传活动，现场的“抽卡有奖游戏”特别引人注目，游戏规则是：盒子中装有8张形状大小相同的精美卡片，卡片上分别印有“世博会吉祥物海宝”或“世博会会徽”，要求两人一组参加游戏，参加游戏的两人从盒子中轮流抽取卡片，一次抽1张，抽取后不放回，直到两人中的一人抽到 “世博会会徽”卡得奖才终止游戏．

　 (Ⅰ)游戏开始之前，一位高中生问：“盒子中有几张‘世博会会徽’卡?”主持人说：“若从盒中任抽2张卡片不都是‘世博会会徽’卡的概率为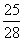”请你回答有几张“世博会会徽”卡呢?

　 (Ⅱ)在(Ⅰ)的条件下，甲、乙两人参加游戏，双方约定甲先抽取乙后抽取，求甲获奖的概率．

19．(本小题满分12分)

已知数列{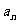}满足条件：a₁＝1，＝2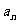+1，n∈N﹡．

　 (Ⅰ)求证：数列{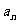+1}为等比数列；

　 (Ⅱ)令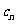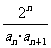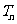＝，是数列{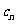}的前n项和，证明 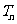＜1.

18．(本小题满分12分)

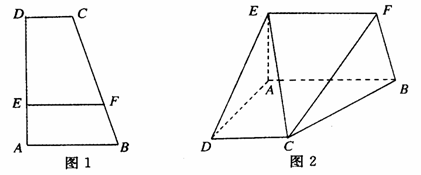　　 如图1，在直角梯形ABCD中，AB∥CD，∠BAD＝90°，AB＝2，AD＝3，CD＝1，点E、F分别在AD、BC上，且AE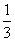＝AD,BF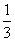＝BC．现将此梯形沿EF折至使AD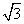＝的位置(如图2)．

　 (Ⅰ)求证：AE⊥平面ABCD；

　 (Ⅱ)求直线CE与平面BCF所成角的正弦值．

17．(本小题满分10分)

在△ABC中，a、b、c分别是角A、B、C的对边，m＝(2b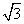－c，cosC)，n＝

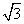(a，cosA)，且m∥n．

　 (Ⅰ)求角A的大小；

　 (Ⅱ)求2cos 2B+sin(A－2B)的最小值．