
2010年2月14日是中国传统的节日--大年初一。中国的春节,是最具文化内涵和传统魅力的节日,也是最有凝聚力的一个节日,回答1~2题。
1、图1中最有可能表示中华民族欢度春节时的光照图是( )
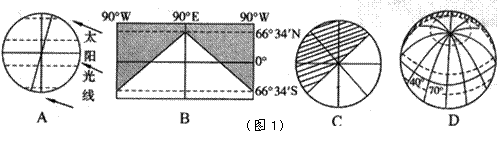
2、当新年钟声敲响时,小华收到了在外国留学的表兄于当地时间2010年2月13日8时发来的短信祝福,小华的表兄最有可能留学在( )
A.美国 B.印度 C.瑞典 D.澳大利亚
23、(10分)已知△ABC的三边长为有理数
(1)求证cosA是有理数
(2)对任意正整数n,求证cosnA也是有理数
(1)设三边长分别为 ,
,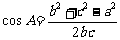 ,∵
,∵ 是有理数,
是有理数, 均可表示为
均可表示为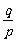 (
(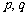 为互质的整数)形式∴
为互质的整数)形式∴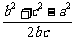 必能表示为
必能表示为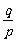 (
(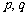 为互质的整数)形式,∴cosA是有理数
为互质的整数)形式,∴cosA是有理数
(2)∵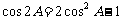 ,∴
,∴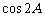 也是有理数,
也是有理数,
当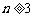 时,∵
时,∵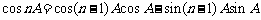
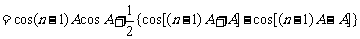
∴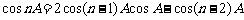 ,
,
∵cosA,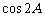 是有理数,∴
是有理数,∴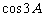 是有理数,∴
是有理数,∴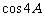 是有理数,……,依次类推,当
是有理数,……,依次类推,当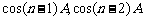 为有理数时,
为有理数时,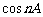 必为有理数。
必为有理数。


全 品中考网

23、(10分)某厂生产甲、乙两种产品,生产甲产品一等品80%,二等品20%;生产乙产品,一等品90%,二等品10%。生产一件甲产品,如果是一等品可获利4万元,若是二等品则要亏损1万元;生产一件乙产品,如果是一等品可获利6万元,若是二等品则要亏损2万元。设生产各种产品相互独立
(3)记x(单位:万元)为生产1件甲产品和件乙产品可获得的总利润,求x的分布列
(4)求生产4件甲产品所获得的利润不少于10万元的概率
解:(1)
|
X |
10 |
5 |
2 |
-3 |
|
P |
0.72 |
0.18 |
0.08 |
0.02 |
(2)依题意,至少需要生产3件一等品
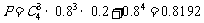
答:…………
22、(10分)某厂生产甲、乙两种产品,生产甲产品一等品80%,二等品20%;生产乙产品,一等品90%,二等品10%。生产一件甲产品,如果是一等品可获利4万元,若是二等品则要亏损1万元;生产一件乙产品,如果是一等品可获利6万元,若是二等品则要亏损2万元。设生产各种产品相互独立
(1)记x(单位:万元)为生产1件甲产品和件乙产品可获得的总利润,求x的分布列
(2)求生产4件甲产品所获得的利润不少于10万元的概率
20.(16分)设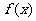 使定义在区间
使定义在区间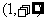 上的函数,其导函数为
上的函数,其导函数为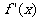 .如果存在实数
.如果存在实数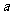 和函数
和函数 ,其中
,其中 对任意的
对任意的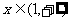 都有
都有 >0,使得
>0,使得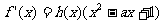 ,则称函数
,则称函数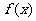 具有性质
具有性质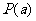 .
.
(1)设函数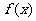
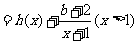 ,其中
,其中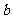 为实数
为实数
①求证:函数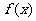 具有性质
具有性质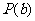
②求函数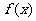 的单调区间
的单调区间
(2)已知函数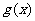 具有性质
具有性质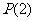 ,给定
,给定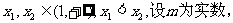
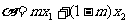 ,
,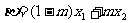 ,且
,且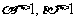 ,若|
,若| |<|
|<| |,求
|,求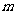 的取值范围
的取值范围
(1)估计该问题目有错,似乎为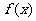
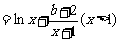 ,则有如下解答:
,则有如下解答:
①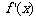
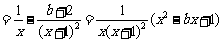
∵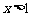 时,
时,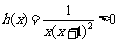 恒成立,
恒成立,
∴函数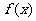 具有性质
具有性质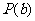

[理科附加题]
21(从以下四个题中任选两个作答,每题10分)
(1)几何证明选讲
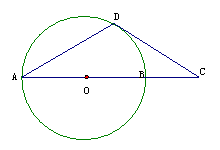
AB是⊙O的直径,D为⊙O上一点,过点D作⊙O的切线交AB延长线于C,若DA=DC,求证AB=2BC
(2)矩阵与变换
在平面直角坐标系xOy中,A(0,0),B(-3,),C(-2,1),设k≠0,k∈R,M= ,N=
,N= ,点A、B、C在矩阵MN对应的变换下得到点A1,B1,C1,△A1B1C1的面积是△ABC面积的2倍,求实数k的值
,点A、B、C在矩阵MN对应的变换下得到点A1,B1,C1,△A1B1C1的面积是△ABC面积的2倍,求实数k的值
(3)参数方程与极坐标
在极坐标系中,圆ρ=2cosθ与直线3ρcosθ+4ρsinθ+a=0相切,求实数a的值
(4)不等式证明选讲
已知实数a,b≥0,求证: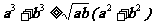
19.(16分)设各项均为正数的数列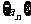 的前n项和为
的前n项和为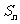 ,已知
,已知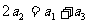 ,数列
,数列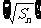 是公差为
是公差为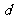 的等差数列.
的等差数列.
①求数列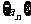 的通项公式(用
的通项公式(用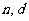 表示)
表示)
②设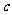 为实数,对满足
为实数,对满足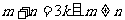 的任意正整数
的任意正整数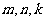 ,不等式
,不等式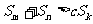 都成立。求证:
都成立。求证: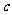 的最大值为
的最大值为

18. (16分)在平面直角坐标系
(16分)在平面直角坐标系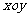 中,如图,已知椭圆
中,如图,已知椭圆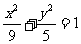 的左右顶点为A,B,右顶点为F,设过点T(
的左右顶点为A,B,右顶点为F,设过点T(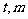 )的直线TA,TB与椭圆分别交于点M
)的直线TA,TB与椭圆分别交于点M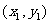 ,
,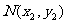 ,其中m>0,
,其中m>0,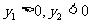
①设动点P满足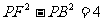 ,求点P的轨迹
,求点P的轨迹
②设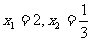 ,求点T的坐标
,求点T的坐标
③设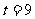 ,求证:直线MN必过x轴上的一定点
,求证:直线MN必过x轴上的一定点
(其坐标与m无关)
 直线
直线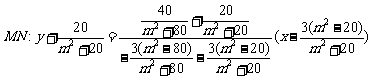 ,
,
化简得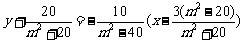
令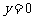 ,解得
,解得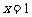 ,即直线
,即直线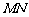 过
过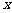 轴上定点
轴上定点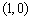 。
。
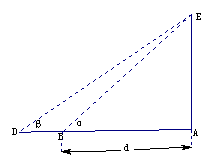
17、(14分)某兴趣小组测量电视塔AE的高度H(单位m),如示意图,垂直放置的标杆BC高度h=4m,仰角∠ABE=α,∠ADE=β
(1)该小组已经测得一组α、β的值,tanα=1.24,tanβ=1.20,,请据此算出H的值
(2)该小组分析若干测得的数据后,发现适当调整标杆到电视塔的距离d(单位m),使α与β之差较大,可以提高测量精确度,若电视塔实际高度为125m,问d为多少时,α-β最大
16、(14分)如图,四棱锥P-ABCD中,PD⊥平面ABCD,PD=DC=BC=1,AB=2,AB∥DC,∠BCD=900
(1)求证:PC⊥BC
(2)求点A到平面PBC的距离

解析:(1)∵PD⊥平面ABCD,∴ ,又
,又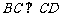 ,∴
,∴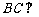 面
面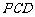 ,∴
,∴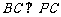 。
。
(2)设点A到平面PBC的距离为 ,
,
∵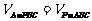 ,∴
,∴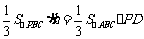
容易求出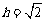
15、(14分)在平面直角坐标系xOy中,点A(-1,-2),B(2,3),C(-2,-1)
(1)求以线段AB、AC为邻边的平行四边形两条对角线的长
(2)设实数t满足(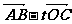 )·
)·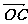 =0,求t的值
=0,求t的值
解析:(1)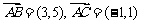
求两条对角线长即为求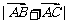 与
与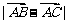 ,
,
由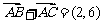 ,得
,得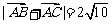 ,
,
由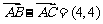 ,得
,得
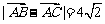 。
。
(2)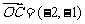 ,
,
∵(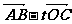 )·
)·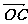
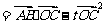 ,
,
易求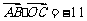 ,
,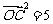 ,
,
所以由(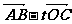 )·
)·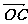 =0得
=0得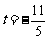 。
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com