
组成生物体的化学元素主要以化合物的形式存在。化合物分为无机化合物和有机化合物两大类,无机化合物包括水和无机盐,有机化合物包括糖类、脂质、核酸和蛋白质。
各种化合物在生物体内的含量不同,水的含量最多,其次是蛋白质。每种化合物都有其重要的生理功能,但是任何一种化合物都不能够单独地完成某一种生命活动,只有按照一定的方式有机地组织起来,才能表现出细胞和生物体的生命现象。
4.各种元素在生物体内的存在形式及功能不同。有的以离子状态调节机体的生理功能(如K+在植物体内促进糖类物质向根茎部分运输),还有的兼有多种功能,如Mg是叶绿素的组成成分,Mg2+是调节体液平衡的因素之一,还是许多酶的激活因子。多数的元素以化合物的形式构成生物体:由C、H、O构成的糖类、脂类,由C、H、O、N、S构成的蛋白质以及由C、H、O、N、P构成的核酸等是构成细胞和生物体的重要组成物质,也是生物体生命活动的物质基础。
知识拓展 微量元素与人体健康
人体内的微量元素虽然含量很少,但对人体健康却起着重要作用。它们作为酶、激素、维生素和核酸的成分,参与生命的代谢过程。从某种意义上说,微量元素比维生素对机体更重要。目前已发现的微量元素有20余种,已知铁、碘、铜、锰、锌、钴、铬、硒、铝、氟、硅、锡、钒等微量元素与机体的生命活动关系密切。
(1)在酶系统中起特异的活化中心作用。
(2)在激素和维生素中起特异的生理作用。
(3)输送元素的作用。
(4)调节体液渗透压和酸碱平衡。
(5)影响核酸代谢。
(6)防癌、抗癌作用。
3.在组成细胞的元素中,C、O、H、N这四种元素的含量最多。在干重中碳元素的含量达到48.4%。这表明C是构成细胞的基本元素。
难点剖析C元素是构成生物体的主要成分之一。C原子含有6个质子、6个中子和6个电子。C原子的4个价电子可与许多原子结合,但主要是与H、O、N和S结合,也可以与其他C原子形成共价键。C和C之间以共价键形成的长链可以是直链,也可以是支链。相邻的C原子之间还可以结合成双键或三键。种类繁多的生物大分子都是以C链为基本骨架的。生物大分子,如多糖、蛋白质和核酸都是由许多基本组成单位(又叫单体)连接而成的多聚体。
2.微量元素通常指生物生活所必需,但是需要量却很少的一些元素,例如Fe、Mn、B、Zn、Cu、Mo、Cl、Ni等。这些元素虽然含量少,但如果缺失,会对生物体造成各种各样的伤害。例如硒能保护心脏,防止心肌纤维化,改善心房收缩和舒张性能,调整心率。如果缺硒,心肌受损造成心肌增大,急性或慢性心功能不全和各种类型的心率失常,急重症可导致死亡。
1.大量元素是指含量占生物体元素总量万分之一以上的元素。 地球上天然存在的元素有90多种,在细胞中可找到至少62种元素,其中重要的有24种,常见的有29种。在生物体的元素构成中,C、H、O、N、P、S、K、Ca、Mg等元素属于大量元素。
2.竖直上抛运动
物体以某一初速度竖直向上抛出,只在重力作用下的运动。
(1)特点:初速度为v0,加速度为 -g的匀变速直线运动。
(2)规律:vt= v0-gt h = v0t-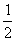 gt2 vt2-
v02=-2gh
gt2 vt2-
v02=-2gh
上升时间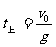 ,下降到抛出点的时间
,下降到抛出点的时间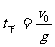 ,上升最大高度
,上升最大高度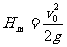
(3)处理方法:
一是将竖直上抛运动全过程分为上升和下降两个阶段来处理,要注意两个阶段运动的对称性。
二是将竖直上抛运动全过程视为初速度为v0,加速度为 -g的匀减速直线运动
综合应用例析
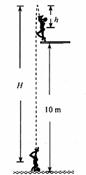 [例11]一跳水运动员从离水面10m高的平台上向上跃起,举双臂直体离开台面,此时其重心位于从手到脚全长的中点,跃起后重心升高0.45m达到最高点,落水时身体竖直,手先入水(在此过程中运动员水平方向的运动忽略不计)从离开跳台到手触水面,他可用于完成空中动作的时间是______s。(计算时,可以把运动员看作全部质量集中在重心的一个质点,g取10m/s2,结果保留二位数)
[例11]一跳水运动员从离水面10m高的平台上向上跃起,举双臂直体离开台面,此时其重心位于从手到脚全长的中点,跃起后重心升高0.45m达到最高点,落水时身体竖直,手先入水(在此过程中运动员水平方向的运动忽略不计)从离开跳台到手触水面,他可用于完成空中动作的时间是______s。(计算时,可以把运动员看作全部质量集中在重心的一个质点,g取10m/s2,结果保留二位数)
解析: 运动员的跳水过程是一个很复杂的过程,主要是竖直方向的上下运动,但也有水平方向的运动,更有运动员做的各种动作。构建运动模型,应抓主要因素。现在要讨论的是运动员在空中的运动时间,这个时间从根本上讲与运动员所作的各种动作以及水平运动无关,应由竖直运动决定,因此忽略运动员的动作,把运动员当成一个质点,同时忽略他的水平运动。当然,这两点题目都作了说明,所以一定程度上“建模”的要求已经有所降低,但我们应该理解这样处理的原因。这样,我们把问题提炼成了质点作竖直上抛运动的物理模型。
在定性地把握住物理模型之后,应把这个模型细化,使之更清晰。可画出如图所示的示意图。由图可知,运动员作竖直上抛运动,上升高度h,即题中的0.45m;从最高点下降到手触到水面,下降的高度为H,由图中H、h、10m三者的关系可知H=10.45m。
由于初速未知,所以应分段处理该运动。运动员跃起上升的时间为: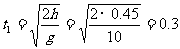 s
s
从最高点下落至手触水面,所需的时间为: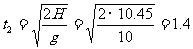 s
s
所以运动员在空中用于完成动作的时间约为: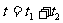 =1.7s
=1.7s
点评:构建物理模型时,要重视理想化方法的应用,要养成化示意图的习惯。
 [例12]如图所示是我国某优秀跳水运动员在跳台上腾空而起的英姿.跳台距水面高度为10 m,此时她恰好到达最高位置,估计此时她的重心离跳台台面的高度为1 m,当她下降到手触及水面时要伸直双臂做一个翻掌压水花的动作,这时她的重心离水面也是1 m.(取g=10 m/s2)求:
[例12]如图所示是我国某优秀跳水运动员在跳台上腾空而起的英姿.跳台距水面高度为10 m,此时她恰好到达最高位置,估计此时她的重心离跳台台面的高度为1 m,当她下降到手触及水面时要伸直双臂做一个翻掌压水花的动作,这时她的重心离水面也是1 m.(取g=10 m/s2)求:
(1)从最高点到手触及水面的过程中其重心可以看作是自由落体运动,她在空中完成一系列动作可利用的时间为多长?
(2)忽略运动员进入水面过程中受力的变化,入水之后,她的重心能下沉到离水面约2.5 m处,试估算水对她的平均阻力约是她自身重力的几倍?
解析:(1)这段时间人重心下降高度为10 m
空中动作时间t=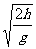
代入数据得t=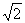 s=1.4 s
s=1.4 s
(2)运动员重心入水前下降高度 h+Δh=11 m
据动能定理mg(h+Δh+h水)=fh水
整理并代入数据得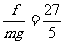 =5.4
=5.4
1.自由落体运动
物体由静止开始,只在重力作用下的运动。
(1)特点:加速度为g,初速度为零的匀加速直线运动。
(2)规律:vt=gt h =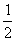 gt2
vt2
=2gh
gt2
vt2
=2gh
6、解题方法指导:
解题步骤:
(1)根据题意,确定研究对象。
(2)明确物体作什么运动,并且画出运动示意图。
(3)分析研究对象的运动过程及特点,合理选择公式,注意多个运动过程的联系。
(4)确定正方向,列方程求解。
(5)对结果进行讨论、验算。
解题方法:
(1)公式解析法:假设未知数,建立方程组。本章公式多,且相互联系,一题常有多种解法。要熟记每个公式的特点及相关物理量。
(2)图象法:如用v-t图可以求出某段时间的位移大小、可以比较vt/2与vS/2,以及追及问题。用s-t图可求出任意时间内的平均速度。
(3)比例法:用已知的讨论,用比例的性质求解。
(4)极值法:用二次函数配方求极值,追赶问题用得多。
(5)逆向思维法:如匀减速直线运动可视为反方向的匀加速直线运动来求解。
综合应用例析
[例1]在光滑的水平面上静止一物体,现以水平恒力甲推此物体,作用一段时间后换成相反方向的水平恒力乙推物体,当恒力乙作用时间与恒力甲的作用时间相同时,物体恰好回到原处,此时物体的速度为v2,若撤去恒力甲的瞬间物体的速度为v1,则v2∶v1=?
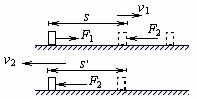
解析:解决此题的关键是:弄清过程中两力的位移关系,因此画出过程草图(如图5),标明位移,对解题有很大帮助。
通过上图,很容易得到以下信息:
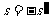 ,而
,而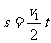 ,
,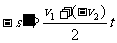 得v2∶v1=2∶1
得v2∶v1=2∶1
思考:在例1中,F1、F2大小之比为多少?(答案:1∶3)
点评:特别要注意速度的方向性。平均速度公式和加速度定义式中的速度都是矢量,要考虑方向。本题中以返回速度v1方向为正,因此,末速度v2为负。
[例2] 两木块自左向右运动,现用高速摄影机在同一底片上多次曝光,记录下木块每次曝光时的位置,如图所示,连续两次曝光的时间间隔是相等的,由图可知
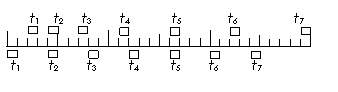
A.在时刻t2以及时刻t5两木块速度相同
B.在时刻t1两木块速度相同
C.在时刻t3和时刻t4之间某瞬间两木块速度相同
D.在时刻t4和时刻t5之间某瞬时两木块速度相同
解析:首先由图看出:上边那个物体相邻相等时间内的位移之差为恒量,可以判定其做匀变速直线运动;下边那个物体明显地是做匀速运动。由于t2及t5时刻两物体位置相同,说明这段时间内它们的位移相等,因此其中间时刻的即时速度相等,这个中间时刻显然在t3、t4之间,因此本题选C。
[例3] 在与x轴平行的匀强电场中,一带电量q=1.0×10-8C、质量m=2.5×10-3kg的物体在光滑水平面上沿着x轴作直线运动,其位移与时间的关系是x=0.16t-0.02t2,式中x以m为单位,t以s为单位。从开始运动到5s末物体所经过的路程为 m,克服电场力所做的功为 J。
解析:须注意:本题第一问要求的是路程;第二问求功,要用到的是位移。
将x=0.16t-0.02t2和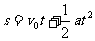 对照,可知该物体的初速度v0=0.16m/s,加速度大小a=0.04m/s2,方向跟速度方向相反。由v0=at可知在4s末物体速度减小到零,然后反向做匀加速运动,末速度大小v5=0.04m/s。前4s内位移大小
对照,可知该物体的初速度v0=0.16m/s,加速度大小a=0.04m/s2,方向跟速度方向相反。由v0=at可知在4s末物体速度减小到零,然后反向做匀加速运动,末速度大小v5=0.04m/s。前4s内位移大小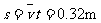 ,第5s内位移大小
,第5s内位移大小 ,因此从开始运动到5s末物体所经过的路程为0.34m,而位移大小为0.30m,克服电场力做的功W=mas5=3×10-5J。
,因此从开始运动到5s末物体所经过的路程为0.34m,而位移大小为0.30m,克服电场力做的功W=mas5=3×10-5J。
[例4]一辆汽车沿平直公路从甲站开往乙站,起动加速度为2m/s2,加速行驶5秒,后匀速行驶2分钟,然后刹车,滑行50m,正好到达乙站,求汽车从甲站到乙站的平均速度?
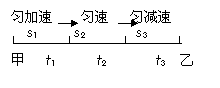 解析:起动阶段行驶位移为:
解析:起动阶段行驶位移为:
s1=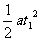 ……(1)
……(1)
匀速行驶的速度为: v= at1 ……(2)
匀速行驶的位移为: s2 =vt2 ……(3)
刹车段的时间为: s3 =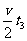 ……(4)
……(4)
汽车从甲站到乙站的平均速度为:
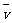 =
=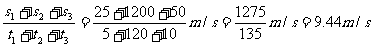
[例5]汽车以加速度为2m/s2的加速度由静止开始作匀加速直线运动,求汽车第5秒内的平均速度?
解析:此题有三解法:
(1)用平均速度的定义求:
第5秒内的位移为: s = 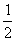 a
t52 -
a
t52 -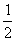 at42
=9 (m)
at42
=9 (m)
第5秒内的平均速度为: v=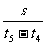 =
=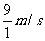 =9 m/s
=9 m/s
(2)用推论v=(v0+vt)/2求:v=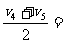
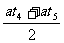 =
=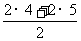 m/s=9m/s
m/s=9m/s
(3)用推论v=vt/2求。第5秒内的平均速度等于4.5s时的瞬时速度:
v=v4.5= a´4.5=9m/s
[例6]一物体由斜面顶端由静止开始匀加速下滑,最初的3秒内的位移为s1,最后3秒内的位移为s2,若s2-s1=6米,s1∶s2=3∶7,求斜面的长度为多少?
解析:设斜面长为s,加速度为a,沿斜面下滑的总时间为t 。则:
斜面长: s = 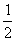 at2 …… ( 1)
at2 …… ( 1)
前3秒内的位移:s1 = 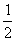 at12 ……(2)
at12 ……(2)
|


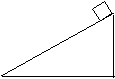 后3秒内的位移: s2 =s -
后3秒内的位移: s2 =s -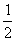 a (t-3)2 …… (3)
a (t-3)2 …… (3)
|
s1∶s2 = 3∶7 …… (5)
解(1)-(5)得:a=1m/s2 t= 5s s=12 . 5m
[例7]物块以v0=4米/秒的速度滑上光滑的斜面,途经A、B两点,已知在A点时的速度是B点时的速度的2倍,由B点再经0.5秒物块滑到斜面顶点C速度变为零,A、B相距0.75米,求斜面的长度及物体由D运动到B的时间?
解析:物块作匀减速直线运动。设A点速度为VA、B点速度VB,加速度为a,斜面长为S。
 A到B: vB2 - vA2 =2asAB ……(1)
A到B: vB2 - vA2 =2asAB ……(1)
vA = 2vB ……(2)
B到C: 0=vB + at0 ……..(3)
解(1)(2)(3)得:vB=1m/s
a= -2m/s2
D到C 0 - v02=2as ……(4)
s= 4m
从D运动到B的时间:
D到B: vB =v0+ at1 t1=1.5秒
D到C再回到B:t2 = t1+2t0=1.5+2´0.5=2.5(s)
[例8]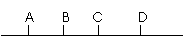 一质点沿AD直线作匀加速直线运动,如图,测得它在AB、BC、CD三段的时间均为t,测得位移AC=L1,BD=L2,试求质点的加速度?
一质点沿AD直线作匀加速直线运动,如图,测得它在AB、BC、CD三段的时间均为t,测得位移AC=L1,BD=L2,试求质点的加速度?
解析:设AB=s1、BC=s2、CD=s3 则:
s2-s1=at2 s3-s2=at2
两式相加:s3-s1=2at2
由图可知:L2-L1=(s3+s2)-(s2+s1)=s3-s1
则:a = 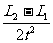
[例9]一质点由A点出发沿直线AB运动,行程的第一部分是加速度为a1的匀加速运动,接着做加速度为a2的匀减速直线运动,抵达B点时恰好静止,如果AB的总长度为s,试求质点走完AB全程所用的时间t?
解析:设质点的最大速度为v,前、后两段运动过程及全过程的平均速度相等,均为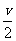 。
。
全过程: s= ……(1)
……(1)
匀加速过程:v = a1t1 ……(2)
匀减速过程:v = a2t2 ……(3)
由(2)(3)得:t1=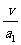
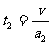 代入(1)得:
代入(1)得:
s = 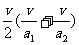 s=
s=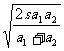
将v代入(1)得:
t = 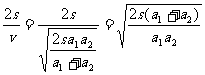
[例10]一个做匀加速直线运动的物体,连续通过两段长为s的位移所用的时间分别为t1、t2,求物体的加速度?
解析:
方法一:
设前段位移的初速度为v0,加速度为a,则:
前一段s: s=v0t1
+ 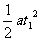 ……(1)
……(1)
全过程2s: 2s=v0(t1+t2)+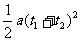 ……(2)
……(2)
消去v0得: a = 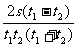
方法二:
设前一段时间t1的中间时刻的瞬时速度为v1,后一段时间t2的中间时刻的瞬时速度为v2。所以:
v1=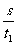 ……(1)
v2=
……(1)
v2=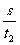 ……(2)
……(2)
v2=v1+a(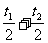 )
……(3)
解(1)(2)(3)得相同结果。
)
……(3)
解(1)(2)(3)得相同结果。
方法三:
设前一段位移的初速度为v0,末速度为v,加速度为a。
前一段s: s=v0t1
+ 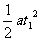 ……(1)
……(1)
后一段s: s=vt2 +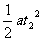 ……(2)
……(2)
v = v0 + at ……(3) 解(1)(2)(3)得相同结果。
5.一种典型的运动
经常会遇到这样的问题:物体由静止开始先做匀加速直线运动,紧接着又做匀减速直线运动到静止。用右图描述该过程,可以得出以下结论:
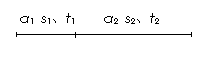 (1)
(1)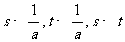
(2)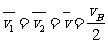
4.初速为零的匀变速直线运动
(1)前1秒、前2秒、前3秒……内的位移之比为1∶4∶9∶……
(2)第1秒、第2秒、第3秒……内的位移之比为1∶3∶5∶……
(3)前1米、前2米、前3米……所用的时间之比为1∶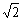 ∶
∶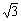 ∶……
∶……
(4)第1米、第2米、第3米……所用的时间之比为1∶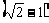 ∶(
∶(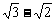 )∶……
)∶……
对末速为零的匀变速直线运动,可以相应的运用这些规律。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com