
5、双曲线方程为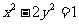 ,则它的右焦点坐标为
,则它的右焦点坐标为
A、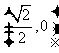 B、
B、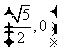 C、
C、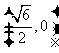 D、
D、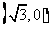
4、若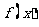 是
是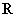 上周期为5的奇函数,且满足
上周期为5的奇函数,且满足 ,则
,则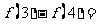
A、-1 B、1 C、-2 D、2
3、设向量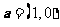 ,
,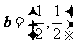 ,则下列结论中正确的是
,则下列结论中正确的是
A、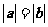 B、
B、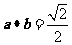
C、 与
与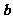 垂直 D、
垂直 D、 ∥
∥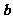
2、若集合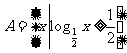 ,则
,则
A、 B、
B、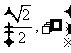
C、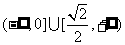 D、
D、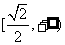
1、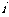 是虚数单位,
是虚数单位,
A、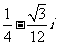 B、
B、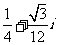 C、
C、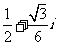 D、
D、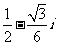
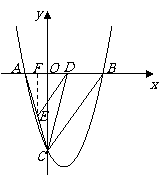
22.解:(1)∵OA、OC的长是x2-5x+4=0的根,OA<OC ∴OA=1,OC=4
∵点A在x轴的负半轴,点C在y轴的负半轴 ∴A(-1,0) C(0,-4)
∵抛物线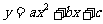 的对称轴为
的对称轴为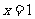 ∴由对称性可得B点坐标为(3,0)
∴由对称性可得B点坐标为(3,0)
∴A、B、C三点坐标分别是:A(-1,0),B(3,0),C(0,-4)
(2)∵点C(0,-4)在抛物线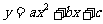 图象上 ∴
图象上 ∴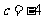
将A(-1,0),B(3,0)代入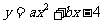 得
得
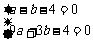 解之得
解之得
∴ 所求抛物线表达式为: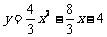
(3)根据题意,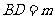 ,则
,则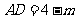 在Rt△OBC中,BC=
在Rt△OBC中,BC=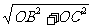 =5
=5
∵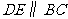 ,∴△ADE∽△ABC
,∴△ADE∽△ABC
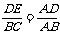 ∴
∴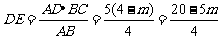
过点E作EF⊥AB于点F,则sin∠EDF=sin∠CBA=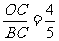
 ∴
∴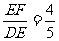 ∴EF=
∴EF=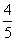 DE=
DE= =4-m
=4-m
∴S△CDE=S△ADC-S△ADE
=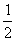 (4-m)×4
(4-m)×4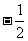 (4-m)( 4-m)
(4-m)( 4-m)
= m2+2m(0<m<4)
m2+2m(0<m<4)
∵S= (m-2)2+2, a=
(m-2)2+2, a= <0
<0
∴当m=2时,S有最大值2.
∴点D的坐标为(1,0).
21.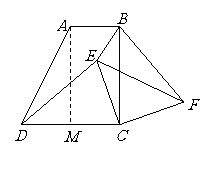 (1)过
(1)过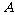 作
作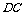 的垂线
的垂线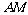 交
交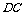 于
于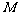 . 则
. 则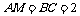 .
.
又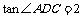 ,所以
,所以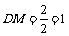 .
.
因为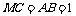 ,所以
,所以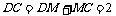 .
.
即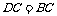 . (2)等腰直角三角形.
. (2)等腰直角三角形.
证明:因为 ,
,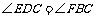 ,
,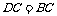 ,
,
所以,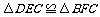 .
.
所以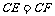 ,
,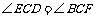 .
.
所以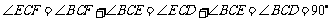 .
.
即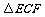 为等腰直角三角形.
为等腰直角三角形.
(3)设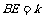 ,则
,则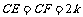 .所以
.所以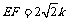 .
.
因为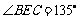 ,又
,又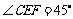 ,所以
,所以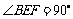 . 所以
. 所以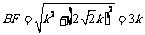 .
.
所以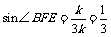 .
.
20. 解:(1)设公司采购了x个大包装箱,y个小包装箱.
根据题意得: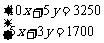 解之得:
解之得: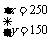
答:公司采购了250个大包装箱,150个小包装箱.
(2)设公司派A种型号的车z辆,则B种型号的车为(10-z)辆.
根据题意得: 解之得:
解之得: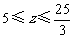
∵ z为正整数 ∴ z取5、6、7、8
∴ 方案一:公司派A种型号的车5辆,B种型号的车5辆.
方案二:公司派A种型号的车6辆,B种型号的车4辆.
方案三:公司派A种型号的车7辆,B种型号的车3辆.
方案四:公司派A种型号的车8辆,B种型号的车2辆.
(3)∵A种车省油,∴应多用A型车,因此最好安排A种车8辆,B种车2辆,即方案四.
19. 解:(1)∵∠A=60°,BD⊥AD ∴∠ABD=30° 又∵AB∥CD ∴∠CDB=∠ABD=30°
∵BC=CD ∴∠CBD=∠CDB=30° (2)∵∠ABD=∠CBD=30°
∴∠ABC=60°=∠A ∴AD=BC=CD=2cm 在Rt△ABD中,∴AB=2AD=4cm
18.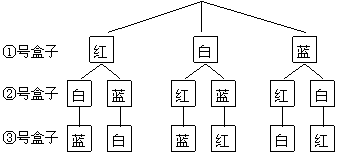 (1)解法1:可画树状图如下:
(1)解法1:可画树状图如下:
共6种情况.
解法2:3个小球分别放入编号为①、②、③的三个盒子的所有可能情况为:红白蓝、红蓝白、白红蓝、白蓝红、蓝红白、蓝白红共6 种.
(2)解:从(1)可知,红球恰好放入 2 号盒子的可能结果有白红蓝、蓝红白共 2种,
所以红球恰好放入2号盒子的概率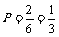 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com