
1. 观察引入
观察课件。你有什么发现?
设计这个问题帮助学生从多个角度考虑问题:
第一:兰鱼是由红鱼被拉长2倍,而宽度没有变。这是从图形形状考虑。
第二:兰鱼的横坐标是红鱼的横坐标的2倍,而他们纵坐标相等。这是从坐标角度考虑。
本节的设计主要考虑到以下几个方面:
3.重点:感受图形坐标变化与图形变换之间的内在关系。
难点:探索在同一坐标系中坐标变化与图形变换之间的内在联系。
2.教学目标
1) 能够由坐标变化对图形进行变换
2) 能够自主探索,与同学进行交流合作
3) 能够使用数学语言有条理地表达自己解决问题的过程。
1.教材的地位和作用
《变化的鱼》是八年级上第五章的最后一节。本节的主要内容是让学生体会坐标变化和图形变换之间的内在联系。在此之前,学生已经知道确定位置需要有两个量,也能对平面直角坐标系的内容有所掌握。如由坐标找点的位置,由点写出坐标,体会到数和形之间的联系,但是这些只是停留在初级阶段,还没有机会把第二章图形的变换和坐标变化联系起来。而本节内容的学习为学生提供了一个契机,让学生体会到知识的连贯性。本节是让学生经历图形坐标变化与图形的变化(如平移,轴对称,伸长,放大等)的探索过程,发展学生的形象思维能力和数形结合的意识。本节的内容在生活中频频出现,学习本节后让他们感觉到数学的作用,能够用数学的眼光观察生活,解决生活中出现的问题。本节的内容对学生后面学习函数及位似图形起到铺垫作用,从而使学生学习函数图象时,都可以帮助他们更好的理解坐标变化与图形变换的关系。
23、(本题满分18分,第(1)小题4分,第(2)小题6分,第(3)小题8分)
在平行四边形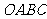 中,已知过点
中,已知过点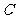 的直线与线段
的直线与线段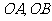 分别相交于点
分别相交于点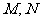 。若
。若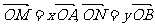 。
。
(1)求证: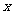 与
与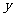 的关系为
的关系为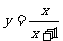 ;
;
(2)设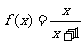 ,定义函数
,定义函数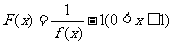 ,点列
,点列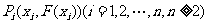 在函数
在函数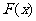 的图像上,且数列
的图像上,且数列 是以首项为1,公比为
是以首项为1,公比为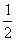 的等比数列,
的等比数列,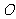 为原点,令
为原点,令 ,是否存在点
,是否存在点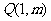
 ,使得
,使得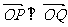 ?若存在,请求出
?若存在,请求出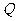 点坐标;若不存在,请说明理由。
点坐标;若不存在,请说明理由。
(3)设函数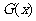 为
为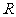 上偶函数,当
上偶函数,当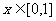 时
时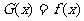 ,又函数
,又函数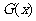 图象关于直线
图象关于直线 对称, 当方程
对称, 当方程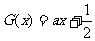 在
在 上有两个不同的实数解时,求实数
上有两个不同的实数解时,求实数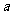 的取值范围。
的取值范围。
22、(本题满分16分,第(1)小题4分,第(2)小题8分,第(3)小题4分)
已知椭圆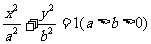 的左右焦点分别为
的左右焦点分别为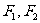 ,短轴两个端点为
,短轴两个端点为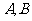 ,且四边形
,且四边形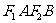 是边长为2的正方形。
是边长为2的正方形。
(1)求椭圆方程;
(2)若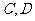 分别是椭圆长轴的左右端点,动点
分别是椭圆长轴的左右端点,动点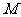 满足
满足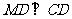 ,连接
,连接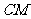 ,交椭圆于点
,交椭圆于点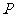 。证明:
。证明: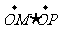 为定值;
为定值;
(3)在(2)的条件下,试问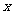 轴上是否存在异于点
轴上是否存在异于点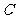 的定点
的定点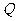 ,使得以
,使得以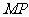 为直径的圆恒过直线
为直径的圆恒过直线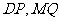 的交点,若存在,求出点
的交点,若存在,求出点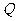 的坐标;若不存在,请说明理由。
的坐标;若不存在,请说明理由。
21、(本题满分16分,第(1)小题6分,第(2)小题10分)
为了让更多的人参与2010年在上海举办的“世博会”,上海某旅游公司面向国内外发行总量为2000万张的旅游优惠卡,其中向境外人士发行的是世博金卡(简称金卡),向境内人士发行的是世博银卡(简称银卡)。现有一个由36名游客组成的旅游团到上海参观旅游,其中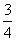 是境外游客,其余是境内游客。在境外游客中有
是境外游客,其余是境内游客。在境外游客中有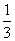 持金卡,在境内游客中有
持金卡,在境内游客中有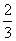 持银卡。.
持银卡。.
(1)在该团中随机采访3名游客,求恰有1人持金卡且持银卡者少于2人的概率;
(2)在该团的境内游客中随机采访3名游客,设其中持银卡人数为随机变量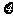 ,求
,求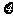 的分布列及数学期望
的分布列及数学期望 。
。
20、(本题满分14分,第(1)小题4分,第(2)小题4分,第(2)小题6分)
设数列 中,若
中,若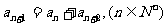 ,则称数列
,则称数列 为“凸数列”。
为“凸数列”。
(1)设数列 为“凸数列”,若
为“凸数列”,若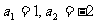 ,试写出该数列的前6项,并求出该6项之和;
,试写出该数列的前6项,并求出该6项之和;
(2)在“凸数列” 中,求证:
中,求证: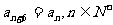 ;
;
(3)设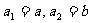 ,若数列
,若数列 为“凸数列”,求数列前
为“凸数列”,求数列前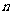 项和
项和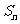 。
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com