
11.在区间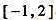 上随机取一个数x,则
上随机取一个数x,则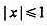 的概率为
的概率为
10.如图1所示,过 外一点P作一条直线与
外一点P作一条直线与 交于A,B两点。已知PA=2,点P到
交于A,B两点。已知PA=2,点P到 的切线上PT=4,则弦的长为 。
的切线上PT=4,则弦的长为 。
9.已知一种材料的最佳入量在110g到210g之间。若用0.618法安排实验,则第一次试点的加入量可以是 g
(18)(本题满分l4分)在△ABC中,角A、B、C所对的边分别为a,b,c,已知
(I)求sinC的值;
(Ⅱ)当a=2, 2sinA=sinC时,求b及c的长.
(19) (本题满分l4分)如图,一个小球从M处投入,通过管道自
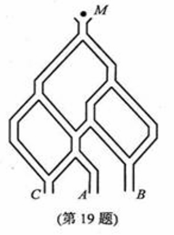 上而下落A或B或C。已知小球从每个叉口落入左右两个
上而下落A或B或C。已知小球从每个叉口落入左右两个
管道的可能性是相等的.
某商家按上述投球方式进行促销活动,若投入的小球落
到A,B,C,则分别设为l,2,3等奖.
(I)已知获得l,2,3等奖的折扣率分别为50%,70%,
90%.记随变量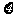 为获得k(k=1,2,3)等奖的折扣
为获得k(k=1,2,3)等奖的折扣
率,求随机变量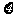 的分布列及期望
的分布列及期望 ;
;
(II)若有3人次(投入l球为l人次)参加促销活动,记随机
 变量
变量 为获得1等奖或2等奖的人次,求
为获得1等奖或2等奖的人次,求 .
.
(20)(本题满分15分)如图, 在矩形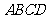 中,点
中,点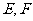 分别
分别
在线段 上,
上,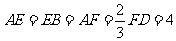 .沿直线
.沿直线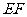
将  翻折成
翻折成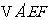 ,使平面
,使平面 .
.
(Ⅰ)求二面角 的余弦值;
的余弦值;
(Ⅱ)点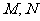 分别在线段
分别在线段 上,若沿直线
上,若沿直线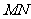 将四
将四
边形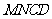 向上翻折,使
向上翻折,使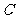 与
与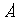 重合,求线段
重合,求线段
的长。
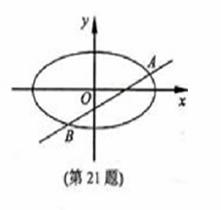 (21) (本题满分15分)已知m>1,直线
(21) (本题满分15分)已知m>1,直线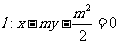 ,
,
椭圆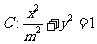 ,
,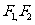 分别为椭圆
分别为椭圆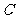 的左、右焦点.
的左、右焦点.
(Ⅰ)当直线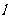 过右焦点
过右焦点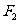 时,求直线
时,求直线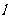 的方程;
的方程;
(Ⅱ)设直线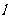 与椭圆
与椭圆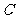 交于
交于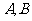 两点,
两点,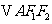 ,
,
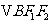 的重心分别为
的重心分别为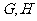 .若原点
.若原点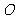 在以线段
在以线段
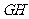 为直径的圆内,求实数
为直径的圆内,求实数 的取值范围.
的取值范围.
(22)(本题满分14分)已知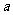 是给定的实常数,设函数
是给定的实常数,设函数 ,
,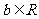 ,
,
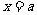 是
是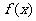 的一个极大值点.
的一个极大值点.
(Ⅰ)求 的取值范围;
的取值范围;
(Ⅱ)设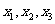 是
是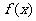 的3个极值点,问是否存在实数
的3个极值点,问是否存在实数 ,可找到
,可找到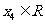 ,使得
,使得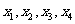 的某种排列
的某种排列 (其中
(其中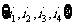 =
= )依次成等差数列?若存在,求所有的
)依次成等差数列?若存在,求所有的 及相应的
及相应的 ;若不存在,说明理由.
;若不存在,说明理由.
 (11)函数
(11)函数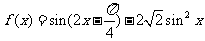 的最小
的最小
正周期是__________________ .
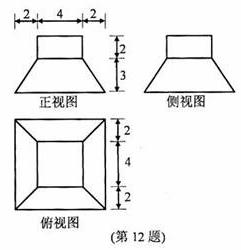
(12)若某几何体的三视图(单位:cm)如图所示,
则此几何体的体积是___________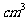 .
.
(13)设抛物线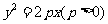 的焦点为
的焦点为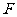 ,点
,点
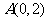 .若线段
.若线段 的中点
的中点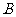 在抛物线上,
在抛物线上,
则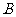 到该抛物线准线的距离为_____________。
到该抛物线准线的距离为_____________。
(14)设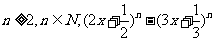
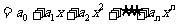 ,
,
将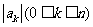 的最小值记为
的最小值记为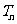 ,则
,则
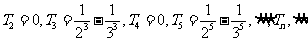
其中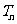 =__________________
.
=__________________
.
(15)设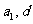 为实数,首项为
为实数,首项为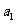 ,公差为
,公差为 的等差数列
的等差数列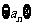 的前
的前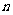 项和为
项和为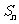 ,满足
,满足 ,
,
则 的取值范围是__________________ .
的取值范围是__________________ .
(16)已知平面向量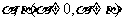 满足
满足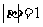 ,且
,且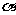 与
与 的夹角为120°,
的夹角为120°,
则 的取值范围是__________________ .
的取值范围是__________________ .
(17)有4位同学在同一天的上、下午参加“身高与体重”、“立定跳远”、“肺活量”、“握力”、
“台阶”五个项目的测试,每位同学上、下午各测试一个项目,且不重复. 若上午不测“握
力”项目,下午不测“台阶”项目,其余项目上、下午都各测试一人. 则不同的安排方式共
有______________种(用数字作答).
 (1)设P={x︱x<4},Q={x︱
(1)设P={x︱x<4},Q={x︱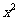 <4},则
<4},则
(A)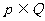 (B)
(B)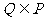
(C) (D)
(D)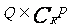
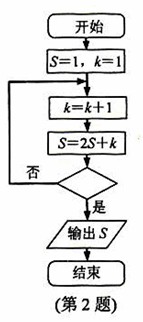
(2)某程序框图如图所示,若输出的S=57,则判断框内位
(A) k>4? (B)k>5?
(C) k>6? (D)k>7?
(3)设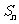 为等比数列
为等比数列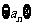 的前
的前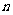 项和,
项和, ,则
,则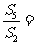
(A)11 (B)5 (C) (D)
(D)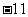
(4)设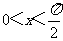 ,则“
,则“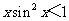 ”是“
”是“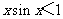 ”的
”的
(A)充分而不必要条件 (B)必要而不充分条件
(C)充分必要条件 (D)既不充分也不必要条件
(5)对任意复数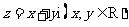 ,
,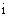 为虚数单位,则下列结论正确的是
为虚数单位,则下列结论正确的是
(A)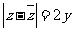 (B)
(B)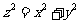
(C) (D)
(D)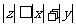
(6)设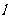 ,
, 是两条不同的直线,
是两条不同的直线,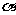 是一个平面,则下列命题正确的是
是一个平面,则下列命题正确的是
(A)若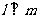 ,
, ,则
,则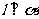 (B)若
(B)若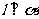 ,
,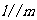 ,则
,则
(C)若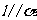 ,
, ,则
,则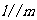 (D)若
(D)若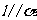 ,
,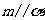 ,则
,则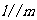
(7)若实数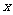 ,
,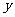 满足不等式组
满足不等式组 且
且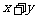 的最大值为9,则实数
的最大值为9,则实数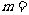
(A) (B)
(B)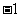 (C)1 (D)2
(C)1 (D)2
(8)设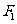 、
、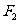 分别为双曲线
分别为双曲线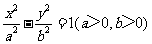 的左、右焦点.若在双曲线右支上存在点
的左、右焦点.若在双曲线右支上存在点 ,满足
,满足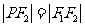 ,且
,且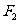 到直线
到直线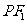 的距离等于双曲线的实轴长,则该双曲线的渐近线方程为
的距离等于双曲线的实轴长,则该双曲线的渐近线方程为
(A)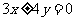 (B)
(B)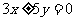 (C)
(C) (D)
(D)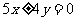
(9)设函数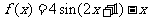 ,则在下列区间中函数
,则在下列区间中函数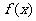 不存在零点的是
不存在零点的是
(A) (B)
(B)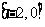 (C)
(C)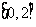 (D)
(D)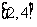
(10)设函数的集合
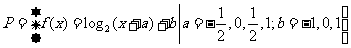 ,
,
平面上点的集合
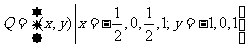 ,
,
则在同一直角坐标系中, 中函数
中函数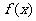 的图象恰好经过
的图象恰好经过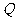 中两个点的函数的个数是
中两个点的函数的个数是
(A)4 (B)6 (C)8 (D)10
绝密★考试结束前
2010年普通高等学校招生全国统一考试
数 学(理科)
非选择题部分(共100分)
22.(本小题满分14分)
正实数数列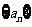 中,
中,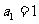 ,
,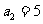 ,且
,且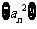 成等差数列.
成等差数列.
(1)证明数列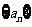 中有无穷多项为无理数;
中有无穷多项为无理数;
(2)当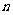 为何值时,
为何值时,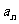 为整数,并求出使
为整数,并求出使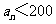 的所有整数项的和.
的所有整数项的和.

21.(本小题满分12分)
如图,已知抛物线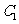 :
: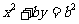 经过椭圆
经过椭圆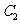 :
: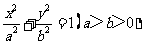 的两个焦点.
的两个焦点.
(1)求椭圆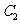 的离心率;
的离心率;
(2)设点 ,又
,又 ,
, 为
为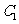 与
与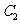 不在
不在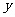 轴上的两个交点,若
轴上的两个交点,若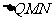 的重心在抛物线
的重心在抛物线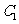 上,求
上,求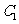 和
和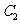 的方程.
的方程.
20.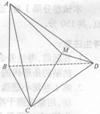 (本小题满分12分)
(本小题满分12分)
如图,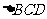 与
与 都是边长为2的正三角形,平面
都是边长为2的正三角形,平面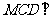 平面
平面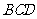 ,
,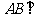 平面
平面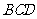 ,
,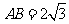 .
.
(1)求直线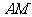 与平面
与平面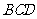 所成角的大小;
所成角的大小;
(2)求平面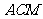 与平面
与平面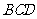 所成二面角的正弦值.
所成二面角的正弦值.
19.(本小题满分12分)
已知函数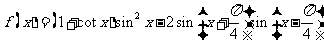 .
.
(1)若 ,求
,求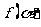 ;
;
(2)若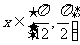 ,求
,求 的取值范围.
的取值范围.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com