
⒖(12分)已知函数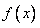 在定义域
在定义域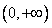 上为增函数,且满足
上为增函数,且满足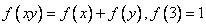 .
.
(1)求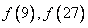 的值;
(2)解不等式:
的值;
(2)解不等式: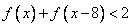 .
.
⒗(12分)已知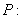 函数
函数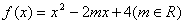 在
在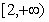 单调递增,
单调递增,
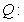 关于
关于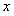 的不等式
的不等式
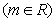 的解集为
的解集为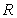 ,
,
若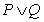 为真命题,
为真命题,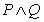 为假命题,求
为假命题,求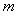 的取值范围.
的取值范围.
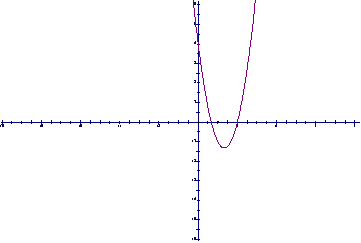
⒘(14分)设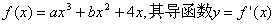 的
的
图象经过点 ,如右图所示。
,如右图所示。
⑴求函数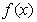 的解析式和极值;
的解析式和极值;
⑵对 恒成立,求实数m的取值范围。
恒成立,求实数m的取值范围。
⒙(14分)我国是水资源比较贫乏的国家之一,各地采用价格调控等手段以达到节约用水的目的。某市用水收费方法是:水费=基本费+超额费+损耗费。该市规定:
①若每月用水量不超过最低限量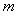 立方米时,只付基本费9元和每户每月的定额损耗费
立方米时,只付基本费9元和每户每月的定额损耗费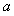 元;
元;
②若每月用水量超过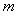 立方米时,除了付基本费和损耗费外,超过部分每立方米付
立方米时,除了付基本费和损耗费外,超过部分每立方米付
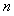 元的超额费;
元的超额费;
③每户每月的损耗费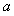 不超过5元。
不超过5元。
⑴求每户每月水费 (元)和用水量
(元)和用水量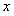 (立方米)的函数关系式;
(立方米)的函数关系式;
⑵该市一家庭去年第一季度的用水量和支付的费用如下表所示:
|
月份 |
用水量(立方米) |
水费(元) |
|
一月份 |
4 |
17 |
|
二月份 |
5 |
23 |
|
三月份 |
2.5 |
11 |
试分析一、二、三各月份的用水量是否超过最低限量,并求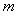 、
、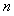 、
、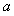 的值。
的值。
⒚(14分)已知函数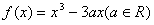 .
.
⑴当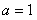 时,求过点
时,求过点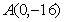 且与函数
且与函数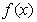 的图象相切的直线
的图象相切的直线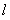 的方程;
的方程;
⑵设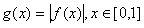 ,求
,求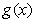 的最大值
的最大值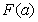 的解析式.
的解析式.
⒛(14分)已知函数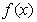 为奇函数,当
为奇函数,当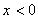 时,
时,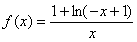 .
.
⑴求当 时,
时,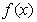 的表达式;
的表达式;
⑵对于任意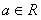 ,比较
,比较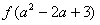 与
与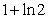 的大小,证明你的结论;
的大小,证明你的结论;
⑶若对任意的 及
及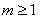 ,不等式
,不等式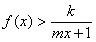 恒成立,求正整数
恒成立,求正整数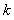 的最大值。
的最大值。
广东省汕头市金山中学
13.(14分)如图所示,两端开口、内壁光滑、长为H的直玻璃管MN竖直固定在水平面上,a、b两个小球直径相等(均略小于玻璃管的内径,且远小于玻璃管的长度),质量分别为m1和m2,且有m1=3m2.开始时,a球在下,b球在上,两球紧挨着在管中从M处由静止同时释放,a球着地后立即反弹,其速度大小不变,方向竖直向上,紧接着与b球相碰使b球竖直上升.设两球碰撞时间极短,碰撞过程中总动能不变.若在b球开始上升的瞬间,一质量为m3的橡皮泥c在M处自由落下,且b与c在管中某处相遇后粘在一起运动.
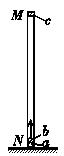 (1)求a、b两球碰撞后瞬间的速度.
(1)求a、b两球碰撞后瞬间的速度.
(2)要使b、c黏合后能够竖直飞出玻璃管口,则m2与m3之比必须满足什么条件?
解析:(1)设管长为H,取向上为正方向,则a、b两球到达玻璃管底端时速度都为:
v0=-
a球着地反弹后瞬间的速度为:
va=
a、b两球相碰前后,由动量守恒定律有:
m1va+m2v0=m1va′+m2vb
又由总动能守恒,有:
m1v+m2v=m1va′2+m2v
代入m1=3m2,可解得:va′=0,vb=.
(2)设c球在M处下落经过时间t后与b球相碰,则有:
vbt-gt2+gt2=H
解得:t=
故b、c两球碰前瞬间的速度分别为:
vb′=-,vc=-
对于b、c两球相碰的过程,由动量守恒定律有:
m2vb′+m3vc=(m2+m3)vbc
要使b、c两球黏合后能飞出管口,则碰后瞬间的速度必须向上,且vbc≥
取vbc=代入上式可得:
m2(-)-m3=(m2+m3)
解得:m2∶m3=1∶3
因此,要使b、c黏合后能够竖直飞出玻璃管口,必须满足条件:>.
答案:(1) (2)>
12. (13分)如图所示,一辆质量为m=2 kg的平板车左边放有质量M=3 kg的滑块,滑块与平板车间的动摩擦因数μ=0.4,开始时平板车和滑块以v0=2 m/s的共同速度在光滑水平面上向右运动,并与竖直墙发生碰撞.设碰撞时间极短,且碰后平板车的速度大小保持不变,但方向与原来相反,平板车足够长,以至滑块不会滑到平板车的右端,取g=10 m/s2.则
(13分)如图所示,一辆质量为m=2 kg的平板车左边放有质量M=3 kg的滑块,滑块与平板车间的动摩擦因数μ=0.4,开始时平板车和滑块以v0=2 m/s的共同速度在光滑水平面上向右运动,并与竖直墙发生碰撞.设碰撞时间极短,且碰后平板车的速度大小保持不变,但方向与原来相反,平板车足够长,以至滑块不会滑到平板车的右端,取g=10 m/s2.则
(1)平板车第一次与墙发生碰撞后向左运动的最大距离为多少?
(2)平板车第二次与墙碰撞前瞬间的速度v为多大?
(3)为使滑块始终不会滑到平板车的右端,平板车至少多长?
解析:(1)第一次碰撞后,由于时间极短,滑块M的速度不变,大小为v0=2 m/s,方向向右;平板车的速度大小为v0,方向向左.然后两者在摩擦力作用下都做减速运动,平板车向左减速到零时,平板车向左运动的距离为最大.设平板车向左运动的最大距离为s,对平板车由动能定理得:
-μMgs=0-
代入数据得:s=0.33 m.
(2)假如平板车在第二次碰撞前还未和滑块相对静止,由运动学知识知,平板车此时的速度大小应为2 m/s,而滑块的速度不小于2 m/s,方向均向右,这样就违背了动量守恒,所以平板车在第二次碰墙前肯定已和滑块具有相同的速度v,由动量守恒得:
Mv0-mv0=(M+m)v
解得:v=0.4 m/s,此速度为平板车在第二次与墙碰前瞬间的速度.
(3)平板车与墙发生多次碰撞,最后停止在墙边,设滑块相对平板车的总位移为L,则有:
=μMgL
代入数据解得:L= m=0.83 m
L即为平板车的最短长度.
答案:(1)0.33 m (2)0.4 m/s (3)0.83 m
11.(13分)40 kg的女孩骑质量为20 kg的自行车带40 kg的男孩(如图所示),行驶速度为3 m/s.自行车行驶时,男孩要从车上下来.
(1)他知道如果直接跳下来,他容易摔跤,为什么?
(2)若他下来时用力往前推自行车,这样他下车时水平速度是零.计算男孩下车的瞬间女孩和自行车的速度.
(3)计算自行车和两个孩子组成的整个系统的动能在男孩下车前后的值.如果不同,请解释.
解析:(1)男孩直接跳下后具有3 m/s的水平速度,脚着地后身体由于惯性容易前倾而摔跤.
(2)设女孩质量为m1,男孩质量为m2,自行车质量为m车,由动量守恒定律得:
(m车+m1+m2)v0=(m车+m1)v1
解得男孩下车瞬间女孩和自行车的速度v1=5 m/s.
(3)Ek=(m车+m1+m2)v=450 J
Ek′=(m车+m1)v=750 J
故知系统动能增加,说明男孩下车时的推力对车及自己总共做的功为:
W=Ek′-Ek=300 J.
答案:略
10.将质量M=3m的木块固定在水平面上,一颗质量为m的子弹以速度v0沿水平方向射入木块,子弹穿出木块时的速度为;现将同样的木块放在光滑的水平面上,相同的子弹仍以速度v0沿水平方向射入木块,则子弹( )
 A.不能射穿木块,子弹和木块以相同的速度做匀速运动
A.不能射穿木块,子弹和木块以相同的速度做匀速运动
B.能射穿木块
C.刚好能射穿木块,子弹射穿木块时速度为零
D.刚好能射穿木块,子弹射穿木块时速度大于
解析:当木块固定时,由动能定理及能量的转化和守恒定律知:
Wf=Q=mv-m()2=mv
假设木块置于光滑水平面时,子弹射穿至木块右端时恰好与木块达到的共同速度,由动量守恒定律得:
mv0=(m+M)v1
解得:v1=
则射穿后子弹与木块的总动能以及射穿过程摩擦生热和为:
E′=·(4m)·()2+mv=mv>mv
这违背了能量的转化和守恒定律,故子弹不可能射穿木块.
答案:A
非选择题部分共3小题,共40分.

9.如图所示,质量相同的两小球A、B均用细线吊在天花板上(A、B两球均不触地).现将小球A拉离平衡位置,使其从高h处由静止开始向下摆动,当它摆至最低点时,恰好与小球B正碰,则碰后B球能升起的高度可能为( )
A. B.h C. D.
解析:当两球发生弹性碰撞时,B球能向左摆至的最大高度hmax=h
当两球发生完全非弹性碰撞时,B球能向左摆至的高度有最小极值hmin,有:
m=2mv
v2=2ghmin
可得:hmin=
故B球能向左摆的高度h′的范围为:≤h′≤h.
答案:ABC
8.  如图所示,两物体A、B用轻质弹簧相连静止在光滑的水平面上,现同时对A、B两物体施加等大、反向的水平恒力F1、F2,使A、B同时由静止开始运动.在运动过程中,对A、B两物体及弹簧组成的系统,下列说法正确的是(整个过程中弹簧不超过其弹性限度)( )
如图所示,两物体A、B用轻质弹簧相连静止在光滑的水平面上,现同时对A、B两物体施加等大、反向的水平恒力F1、F2,使A、B同时由静止开始运动.在运动过程中,对A、B两物体及弹簧组成的系统,下列说法正确的是(整个过程中弹簧不超过其弹性限度)( )
A.动量始终守恒
B.机械能始终守恒
C.当弹簧伸长到最长时,系统的机械能最大
D.当弹力的大小与F1、F2的大小相等时,A、B两物体的速度为零
 解析:A、B及弹簧组成的系统所受的合外力为零,则动量始终守恒,选项A正确;F1、F2对A、B同时做正功或负功,系统的机械能不守恒,选项B错误;因为F1、F2对系统做功之和等于系统机械能的变化,故在弹簧伸长的过程中机械能一直增大,选项C正确;当弹力的大小与F1、F2的大小相等时,A、B的速度最大,选项D错误.
解析:A、B及弹簧组成的系统所受的合外力为零,则动量始终守恒,选项A正确;F1、F2对A、B同时做正功或负功,系统的机械能不守恒,选项B错误;因为F1、F2对系统做功之和等于系统机械能的变化,故在弹簧伸长的过程中机械能一直增大,选项C正确;当弹力的大小与F1、F2的大小相等时,A、B的速度最大,选项D错误.
答案:AC
7.如图所示,一木板静止在光滑水平面上,其右端有一根轻质弹簧沿水平方向与木板相连,木板的质量M=3 kg.一质量m=1 kg的铁块以水平速度v0=4 m/s从木板的左端沿板面向右滑行,压缩弹簧后又被弹回,最后恰好停在木板的左端.在上述过程中,弹簧具有的最大弹性势能为( )
A.3 J B.6 J C.20 J D.4 J
 解析:由动量守恒定律有:mv0=(m+M)vt
解析:由动量守恒定律有:mv0=(m+M)vt
由题意知,系统由于摩擦生热而损失的动能为:
ΔEk=mv-(m+M)v=6 J
故知弹簧压缩最大时摩擦生热损失的动能为:
ΔEk=3 J
此时弹簧的弹性势能最大为:
Ep=mv-ΔEk-(m+M)v=3 J.
答案:A
6. 如图所示,船的质量为M,船上站一质量为m的运动员,运动员要从这静止的船上水平跃出,到达与船水平距离为s、比甲板低h的岸上,至少要做功W,不计水的阻力,则下列说法正确的是( )
如图所示,船的质量为M,船上站一质量为m的运动员,运动员要从这静止的船上水平跃出,到达与船水平距离为s、比甲板低h的岸上,至少要做功W,不计水的阻力,则下列说法正确的是( )
A.如s、h一定,M越大,W越大
B.如s、m和h一定,M越大,W越小
C.如s、M和h一定,W与m成正比
D.如s、m和M一定,h越大,W越小
解析:设运动员要跳上岸所需的最小初速度为v1,此时船的反冲速度为v2,由动量守恒定律有:
Mv2=mv1=p0
其中v1=s
可得:v2=
由能量的转化和守恒定律知,运动员做的功为:
W=Mv+mv=(+).
答案:BD
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com