1.细胞膜具有屏障作用，它可以保护细胞不受外来物质的干扰和有害物质的侵袭。

10.

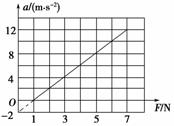
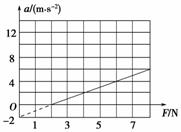
图3－1－16

用水平力拉动物体在水平面上做加速直线运动．当改变拉力的大小时，物体运动的加速度也随之变化，a和F的关系如图3－1－16所示．g取10 m/s².

(1)根据图线所给的信息，求物体的质量及物体与水平面间的动摩擦因数；

(2)若改用质量是原来2倍的同种材料的物体，请在图3－1－16的坐标系上画出这种情况下的a－F图线．(要求写出作图的根据)

解析：(1)根据牛顿第二定律：F－μmg＝ma，所以a＝F－μg

可见a－F图象为一条直线，直线的斜率k＝＝2.0 kg^－1，纵轴截距为－μg＝－2.0 m/s²，

解得：物体的质量m＝0.50 kg，物体与地面间的动摩擦因数μ＝0.20.(也可以用横轴截距求动摩擦因数：当F＝1.0 N时，物体的加速度为零，物体所受阻力F_f＝F＝1.0 N，由F_f＝μmg解得物体与水平面间的动摩擦因数μ＝＝0.20.用其他方法结果正确也可)

(2)当物体质量加倍时，物体的加速度a＝F－μg

直线斜率k′＝＝1.0 kg^－1，纵轴的截距不变，作出如图所示的图线．

答案：(1)0.50 kg　0.20

(2)图见解析

9.

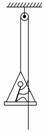
图3－1－15

(2009·安徽，22)在2008年北京残奥会开幕式上运动员手拉绳索向上攀登，最终点燃了主火炬，体现了残疾运动员坚韧不拔的意志和自强不息的精神．为了探求上升过程中运动员与绳索和吊椅间的作用，可将过程简化．一根不可伸缩的轻绳跨过轻质的定滑轮，一端挂一吊椅，另一端被坐在吊椅上的运动员拉住，如图3－1－15所示．设运动员的质量为65 kg，吊椅的质量为15 kg，不计定滑轮与绳子间的摩擦，重力加速度取g＝10 m/s².当运动员与吊椅一起正以加速度a＝1 m/s²上升时，试求：

(1)运动员竖直向下拉绳的力；

(2)运动员对吊椅的压力．

解析：解法一：设运动员和吊椅的质量分别为M和m，绳拉运动员的力为F.以运动员和吊椅整体为研究对象，受到重力的大小为(M+m)g，向上的拉力为2F，根据牛顿第二定律

2F－(M+m)g＝(M+m)a，F＝440 N，根据牛顿第三定律，运动员拉绳的力大小为440 N，方向竖直向下．

(2)以运动员为研究对象，运动员受到三个力的作用，重力大小Mg，绳的拉力F，吊椅对运动员的支持力F_N.根据牛顿第二定律：F+F_N－Mg＝Ma，F_N＝275 N，根据牛顿第三定律，运动员对吊椅的压力大小为275 N，方向竖直向下．

解法二：设运动员和吊椅的质量分别为M和m；运动员竖直向下对绳的拉力大小为F，对吊椅的竖直向下压力大小为F_N.根据牛顿第三定律，绳对运动员的拉力大小为F，吊椅对运动员的支持力大小为F_N.分别以运动员和吊椅为研究对象，根据牛顿第二定律：

F+F_N－Mg＝Ma①

F－F_N－mg＝ma②

由①②解得F＝440 N，F_N＝275 N

答案：(1)440 N，竖直向下　(2)275 N，竖直向下

8.

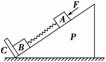
图3－1－14

如图3－1－14所示，在倾角为θ的光滑物块P的斜面上有两个用轻弹簧相连接的物体A和B；C为一垂直固定斜面的挡板，A、B质量均为m，弹簧的劲度系数为k，系统静止在水平面上．现对物体A施加一平行于斜面向下的力F压缩弹簧后，突然撤去外力F，则在物体B刚要离开C时(此过程中A始终没有离开斜面)(　)

A．物体B加速度大小为gsin θ　 　　　　B．弹簧的形变量为mgsin θ/k

C．弹簧对B的弹力大小为mgsin θ　 　 D．物体A的加速度大小为gsin θ

解析：当物体B刚要离开挡板C时，对物体B受力分析可得：kx－mgsin θ＝0，则选项A错误，BC正确；对物体A由牛顿第二定律可得：kx+mgsin θ＝ma_A，解得a_A＝2gsin θ，选项D错误．

答案：BC

7.

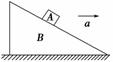
图3－1－13

如图3－1－13所示，物体A与斜面B保持相对静止并一起沿水平面向右做匀加速运动，当加速度a增大时，下列说法可能正确的是(　)

A．B对A的弹力不变，B对A的摩擦力可能减小

B．B对A的弹力增大，B对A的摩擦力大小可能不变

C．B对A的弹力增大，B对A的摩擦力一定增大

D．B对A的弹力增大，B对A的摩擦力可能减小

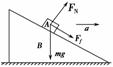
解析：本题考查牛顿第二定律的应用．物体和斜面保持相对静止，沿水平方向加速运动，则合力沿水平方向，竖直方向的合力为零，设斜面的倾角为θ，若开始静摩擦力的方向沿斜面向下，则F_Nsin θ+F_fcos θ＝ma，F_Ncos θ＝F_fsin θ+mg.若N增大，则F_f增大，因此此时，a增大，F_N、F_f都在增大．同理，若开始时静摩擦力方向沿斜面向上，则F_Nsin θ－F_fcos θ＝ma，F_Ncos θ+F_fsin θ＝mg，若F_N逐渐增大，则F_f沿斜面向上先逐渐减小到零，再沿斜面向下逐渐增大，此时B对A的弹力增大，B对A的摩擦力大小可能减小，可能为零，可能不变，可能增大，因此B、D项正确．

答案：BD

6.

图3－1－12

如图3－1－12所示，质量为m的木块在质量为M的长木板上向右滑行，木块受到向右的拉力F的作用，长木板处于静止状态，已知木块与长木板间的动摩擦因数为μ₁，长木板与地面间的动摩擦因数为μ₂，则(　)

A．长木板受到地面的摩擦力的大小一定是μ₁mg

B．长木板受到地面的摩擦力的大小一定是μ₂(m+M)g

C．当F>μ₂(m+M)g时，长木板便会开始运动

D．无论怎样改变F的大小，长木板都不可能运动

解析：木块受到的滑动摩擦力大小为μ₁mg，由牛顿第三定律，长木板受到m对它的摩擦力大小也是μ₁mg，对长木板使用平衡条件得地面对长木板的静摩擦力为μ₂mg，A正确．改变F的大小，木块m受到的滑动摩擦力不会发生变化，长木板受力不变，D正确．

答案：AD

5.

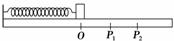
图3－1－11

(2010·广州三校联考)如图3－1－11所示，一条轻质弹簧左端固定，右端系一小物块，物块与水平面各处动摩擦因数相同，弹簧无形变时，物块位于O点．今先后分别把物块拉到P₁和P₂点由静止释放，物块都能运动到O点左方，设两次运动过程中物块速度最大的位置分别为Q₁和Q₂点，则Q₁与Q₂点(　)

A．都在O点　 　　　　　　　　　　　B．都在O点右方，且Q₁离O点近

C．都在O点右方，且Q₂离O点近　 　D．都在O点右方，且Q₁、Q₂在同一位置

解析：物块在水平方向受弹力和滑动摩擦力，弹力是变力，故物块做变加速运动，当加速度a＝0时，速度最大．根据牛顿第二定律，当弹力和摩擦力大小相等，方向相反时，加速度a＝0，故速度最大位置应在O点右方同一位置，故D正确．

答案：D

4.

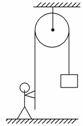
图3－1－10

建筑工人用图3－1－10所示的定滑轮装置运送建筑材料．质量为70.0 kg的工人站在地面上，通过定滑轮将20.0 kg的建筑材料以0.500 m/s²的加速度拉升，忽略绳子和定滑轮的质量及定滑轮的摩擦，则工人对地面的压力大小为(g取10 m/s²)(　)

A．490 N　 　　B．510 N　 　　C．890 N　 　　D．910 N

解析：绳子的拉力T＝mg+ma＝20(10+0.500) N＝210 N．地面对人的支持力也就等于工人对地面的压力大小F_N＝Mg－T＝700 N－210 N＝490 N.

答案：A

3．关于速度、加速度、合外力间的关系，下列说法正确的是(　)

A．物体的速度越大，则加速度越大，所受的合外力也越大

B．物体的速度为零，则加速度为零，所受的合外力也为零

C．物体的速度为零，但加速度可能很大，所受的合外力也可能很大

D．物体的速度很大，但加速度可能为零，所受的合外力也可能为零

解析：加速度由力决定，加速度与速度无必然联系；物体的速度为零时，加速度可以为零，也可以不为零或很大，所以A、B错，C、D对．

答案：CD

2．16世纪末，伽利略用实验和推理，推翻了已在欧洲流行了近两千年的亚里士多德关于力和运动的理论，开启了物理学发展的新纪元．在以下说法中，与亚里士多德观点相反的是(　)

A．四匹马拉的车比两匹马拉的车跑得快；这说明，物体受的力越大，速度就越大

B．一个运动的物体，如果不再受力了，它总会逐渐停下来；这说明，静止状态才是物

体长时间不受力时的“自然状态”

C．两物体从同一高度自由下落，较重的物体下落较快

D．一个物体维持匀速直线运动，不需要受力

解析：亚里士多德认为物体受的力越大，速度就越大；力是物体运动的原因，静止是不受力的自然状态；从同一高度较重的物体下落得较快．物体做匀速直线运动不需要受力与亚里士多德的观点相反，所以本题选D.

答案：D