
20. (本小题满分16分)定义在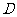 上的函数
上的函数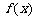 ,如果满足:对任意
,如果满足:对任意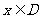 ,存在常数
,存在常数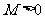 ,都有
,都有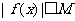 成立,则称
成立,则称 是
是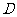 上的有界函数,其中
上的有界函数,其中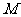 称为函数
称为函数 的上界.
的上界.
已知函数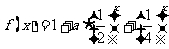 ;
;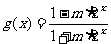 . w w w.ks 5u. c om
. w w w.ks 5u. c om
(1)当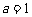 时,求函数
时,求函数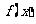 在
在 上的值域,并判断函数
上的值域,并判断函数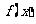 在
在 上是否为有界函数,请说明理由;
上是否为有界函数,请说明理由;
(2)若函数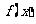 在
在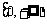 上是以3为上界的有界函数,求实数
上是以3为上界的有界函数,求实数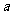 的取值范围;
的取值范围;
(3)若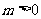 ,函数
,函数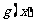 在
在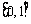 上的上界是
上的上界是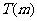 ,求
,求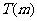 的取值范围.
的取值范围.
B.附加题部分
19. (本小题满分16分)设数列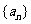 的前n项和为
的前n项和为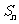 ,数列
,数列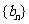 满足:
满足:  ,且数列
,且数列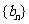 的前
的前
n项和为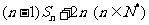 .
.
(1) 求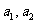 的值;w w w.ks 5u. c om
的值;w w w.ks 5u. c om
(2) 求证:数列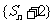 是等比数列;
是等比数列;
(3) 抽去数列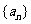 中的第1项,第4项,第7项,……,第3n-2项,……余下的项顺序不变,组成一个新数列
中的第1项,第4项,第7项,……,第3n-2项,……余下的项顺序不变,组成一个新数列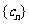 ,若
,若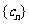 的前n项和为
的前n项和为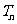 ,求证:
,求证: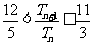 .
.
18. (本小题满分15分)已知椭圆
(本小题满分15分)已知椭圆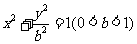 的左焦点为F,左右顶点分别为A、C,
的左焦点为F,左右顶点分别为A、C,
上顶点为B,过F,B,C三点作 ,其中圆心P的坐标为
,其中圆心P的坐标为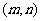 .
.
(1) 若椭圆的离心率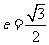 ,求
,求 的方程;w w w.ks 5u. c om
的方程;w w w.ks 5u. c om
(2)若 的圆心在直线
的圆心在直线 上,求椭圆的方程.
上,求椭圆的方程.
17.(本小题满分15分)已知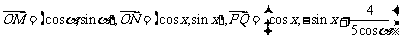
(1)当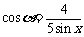 时,求函数
时,求函数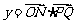 的最小正周期;w w w.ks 5u. c om
的最小正周期;w w w.ks 5u. c om
(2)当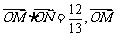 ∥
∥ 时,求
时,求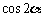 的值.
的值.
16. (本小题满分14分)某工厂三个车间共有工人1000名,各车间男、女工人数如下表:
|
|
第一车间 |
第二车间 |
第三车间 |
|
女工 |
173 |
100 |
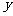 |
|
男工 |
177 |
 |
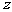 |
已知在全厂工人中随机抽取1名,抽到第二车间男工的概率是0.15.
(1)求 的值;w w w.ks
5u. c om
的值;w w w.ks
5u. c om
(2)现用分层抽样的方法在全厂抽取50名工人,问应在第三车间抽取多少名?
(3)已知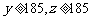 ,求第三车间中女工比男工少的概率.
,求第三车间中女工比男工少的概率.
15.(本小题满分14分)如图ABCD是正方形,O是正方形的中心,PO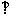 底面ABCD,E是PC的
底面ABCD,E是PC的
中点. 求证:
求证:
(1)PA//平面BDE;w w w.ks 5u. c om
(2)平面PAC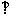 平面BDE.
平面BDE.
14. 用
用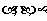 三个字母组成一个长度为
三个字母组成一个长度为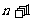
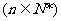 个字母的字符串,要求由
个字母的字符串,要求由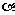 开始,相邻两个字母不同. 例如
开始,相邻两个字母不同. 例如 时,排出的字符串可能是
时,排出的字符串可能是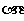 或
或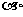 ;
;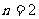 时排出的字符串可能是
时排出的字符串可能是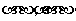
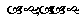 (如图).若记长度为
(如图).若记长度为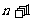 个字母的字符串中,以字母
个字母的字符串中,以字母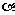 结尾的所有字符串的种数为
结尾的所有字符串的种数为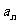 ,
,
如: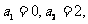 则数列
则数列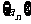 的前
的前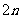 项之和为 ▲ .w w w.ks 5u. c om
项之和为 ▲ .w w w.ks 5u. c om

13.若实数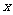 、
、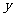 满足
满足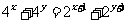 ,则
,则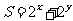 的取值范围是 ▲ .
的取值范围是 ▲ .
12.过直线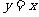 上的一点P作圆
上的一点P作圆 的两条切线
的两条切线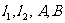 为切点,当直线
为切点,当直线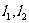 关于直线
关于直线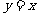 对称时,
对称时,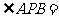 ▲ .
▲ .
11. 在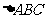 中,已知
中,已知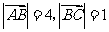 ,
,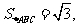 则
则 的值为 ▲ .w w w.ks 5u. c om
的值为 ▲ .w w w.ks 5u. c om
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com