
19.(本小题满分12分)
已知抛物线C的方程C:y 2 =2 p x(p>0)过点A(1,-2).
(I)求抛物线C的方程,并求其准线方程;
(II)是否存在平行于OA(O为坐标原点)的直线l,使得直线l与抛物线C有公共点,且直线OA与l 的距离等于 ?若存在,求出直线l的方程;若不存在,说明理由。
?若存在,求出直线l的方程;若不存在,说明理由。
18.(本小题满分12分)
设平面向量a m =(m,1),b n =(2,n),其中m,n∈{1,2,3,4}.
(I)请列出有序数组(m,n)的所有可能结果;
(II)记“使得a m ⊥(a m-b n)成立的(m,n)”为事件A,求事件A发生的概率.
17.(本小题满分12分)
数列{a n}中,a 1 =1/3,前n项和S n 满足S n+1 -S n =(1 / 3)n + 1 (n∈)N *.
(I)求数列{a n}的通项公式a n 以及前n项和S n
(II)若S 1,t(S 1+ S 2),3(S 2+ S 3)成等差数列,求实数t的值.
16.观察下列等式:
① cos2α=2 cos2 α-1;
② cos 4α=8 cos4 α-8 cos2 α+1;
③ cos 6α=32 cos6 α-48 cos4 α+18 cos2 α-1;
④ cos 8α= 128 cos8α-256cos6 α+160 cos4 α-32 cos2 α+1;
⑤ cos 10α=mcos10α-1280 cos8α+1120cos6 α+ncos4 α+p cos2 α-1;
可以推测,m-n+p= .
15. 对于平面上的点集Ω,如果连接Ω中任意两点的线段必定包涵Ω,则称Ω为平面上的凸集,给出平面上4个点集的图形如下(阴影区域及其边界):
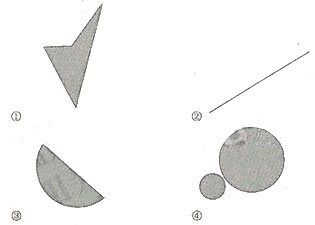
其中为凸集的是 (写出所有凸集相应图形的序号).
14.将容量为n的样本中的数据分成6组. 绘制频率分步直方图.若第一组至第六组数据的频率之比为2:3:4:6:4:1,且前三组数据的频率之和等于27,则n等于 .
13.若双曲线x2 / 4-y2 / b2=1 (b>0) 的渐近线方程为y=±1/2 x ,则b等于 .
23.(本小题为必做题,满分10分)已知数列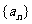 满足:
满足: .
.
(1) 求证: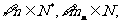 使
使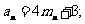
(2) 求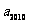 的末位数字.
的末位数字.
22.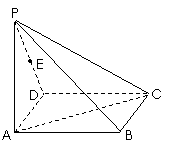 (本小题为必做题,满分10分)如图,在四棱锥
(本小题为必做题,满分10分)如图,在四棱锥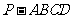 中,底面
中,底面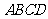 为矩形,侧棱
为矩形,侧棱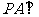 底面
底面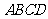 ,
,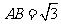 ,
,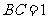 ,
,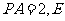 为
为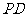 的中点.
的中点.
(1) 求直线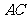 与
与 所成角的余弦值;w w w.ks 5u. c om
所成角的余弦值;w w w.ks 5u. c om
(2) 在侧面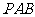 内找一点
内找一点 ,使
,使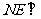 面
面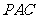 ,并求出点
,并求出点
 到
到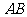 和
和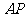 的距离.
的距离.
21.(选做题)从A,B,C,D四个中选做2个,每题10分,共20分.解答时应写出文字说明、证明过程或演算步骤.
 A.(本小题为选做题,满分10分)w w w.ks 5u. c om
A.(本小题为选做题,满分10分)w w w.ks 5u. c om
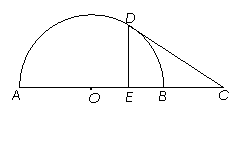
如图,AB是半圆的直径,C是AB延长线上一点,CD
切半圆于点D,CD=2,DE⊥AB,垂足为E,且E是
OB的中点,求BC的长.
B.(本小题为选做题,满分10分)
已知矩阵 ,其中
,其中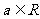 ,若点P(1,1)在矩阵A的变换下得到点
,若点P(1,1)在矩阵A的变换下得到点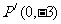 ,
,
(1)求实数a的值; (2)求矩阵A的特征值及特征向量.

C.(本小题为选做题,满分10分)w w w.ks 5u. c om
设点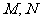 分别是曲线
分别是曲线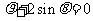 和
和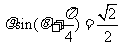 上的动点,求动点
上的动点,求动点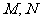 间的最小距离.
间的最小距离.
D.(本小题为选做题,满分10分)
设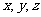 为正数,证明:
为正数,证明: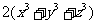 ≥
≥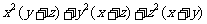 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com