
9. 由乙醇制取乙二酸乙二酯,最简便的流程途径,经下列哪些反应,其顺序正确的是
①取代反应 ②加成反应 ③氧化反应 ④还原反应
⑤消去反应 ⑥酯化反应 ⑦中和反应 ⑧缩聚反应
A.⑤②①③⑥ B.①②③⑤⑦ C.⑤②①④⑧ D.①②⑤③⑥
8. 下列有机物中加入溴水,充分振荡后静置,观察到水层变为无色,有机溶液层为橙黄色,该有机物可能是
A.溴苯 B.油酸甘油酯 C. 丙氨酸 D.蔗糖
7. 有下列一系列稠环化合物:

下列有关叙述中正确的是
A.萘、芘、并蒽属于同系物
B.萘的一溴代物有2种,二溴代物有9种
C.该系列化合物中C、H原子数的最大比值是3,C的质量分数最大值是97.3%
D.从萘开始,这一系列化合物中第25个的分子式为C150H56
6. 用于2008年北京奥运会的国家游泳中心(水立方)的建筑采用了膜材料ETFE,该材料为四氟乙烯与乙烯的共聚物,其化学性质相当稳定,对光、热、酸、碱有很强的耐受性。下列说法中正确的是
A.ETFE分子中可能存在“-CH2-CH2-CF2-CF2-”的连接方式
B.四氟乙烯与乙烯发生缩聚反应得到ETFE
C.ETFE材料是热固型材料
D.ETFE膜材料是纯净物
5. 下列各组物质的相互关系正确的是
A.同位素:1H+、2H+、2H2、2H 3H
B.同分异构体:乙二酸二乙酯、乙二酸乙二酯、二乙酸乙二酯
C.同系物:CH2O2、C2H4O2、C3H6O2、C4H8O2
D.同素异形体:碳纳米管、C60、金刚石、石墨
4. 已知甲酸的酸性比乙酸强。若将碱性定义为接受H+的能力,则下列物质中碱性由强到弱的顺序是①C6H5ONa ②CH3COONa ③C2H5ONa ④Na2CO3 ⑤HCOONa ⑥NaOH
A.③⑥④①②⑤ B.⑥③①④②⑤ C.⑤②①④③⑥ D.③⑥④②①⑤A
3. 可用来鉴别庚烯、邻二甲苯、丙酸乙酯、对甲基苯酚溶液的一组试剂是
A.酸性高锰酸钾溶液、溴水 B.碳酸钠溶液、溴水
C.氯化铁溶液、溴水 D.酸性高锰酸钾溶液、氯化铁溶液
2. 食品保鲜膜按材质分为聚乙烯(PE)、聚氯乙烯(PVC)、聚偏二氯乙烯(PVDC)等种类。PVC被广泛用于食品、蔬菜外包装,它对人体有潜在危害。下列叙述不正确的是
A.PVC保鲜膜属于链状聚合物,在高温时易熔化,能溶于有机溶剂
B.PVC单体可由PE的单体与氯化氢加成制得
C.PVC易发生老化现象,释放出HCl等有害物质,对人体有潜在危害
D.等质量的聚乙烯和乙烯燃烧消耗的氧气相等
1. 化学与生产、生活、社会密切相关。下列有关说法中不正确的是
A.苯酚具有杀菌作用,药皂中也掺有少量苯酚,是因为苯酚可以使蛋白质变性
B.聚氯乙烯凉鞋可以热修补是利用了线型高分子化合物的热塑性
C.乙炔在氧气中燃烧生成的氧炔焰可用于焊接或切割金属
D.2008年诺贝尔化学奖被授予研究“绿色荧光蛋白质”的美籍华裔科学家钱永健等人。蛋白质都是由氨基酸形成的不可降解的高分子化合物
18.(2010湖南文数)(本小题满分12分)
 如图所示,在长方体
如图所示,在长方体 中,AB=AD=1,AA1=2,M是棱CC1的中点
中,AB=AD=1,AA1=2,M是棱CC1的中点
(Ⅰ)求异面直线A1M和C1D1所成的角的正切值;
(Ⅱ)证明:平面ABM⊥平面A1B1M1

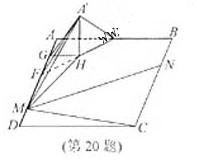
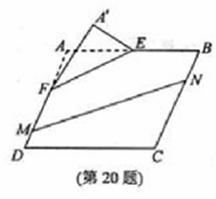 (2010浙江理数)(20)(本题满分15分)如图, 在矩形
(2010浙江理数)(20)(本题满分15分)如图, 在矩形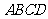 中,点
中,点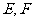 分别在线段
分别在线段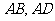 上,
上, .沿直线
.沿直线 将
将 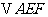 翻折成
翻折成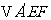 ,使平面
,使平面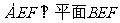 .
.
(Ⅰ)求二面角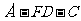 的余弦值;
的余弦值;
(Ⅱ)点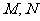 分别在线段
分别在线段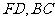 上,若沿直线
上,若沿直线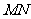 将四边形
将四边形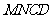 向上翻折,使
向上翻折,使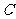 与
与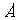 重合,求线段
重合,求线段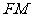 的长。
的长。
解析:本题主要考察空间点、线、面位置关系,二面角等基础知识,空间向量的应用,同事考查空间想象能力和运算求解能力。
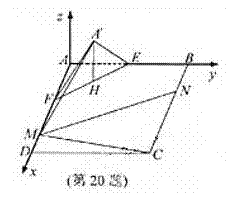 (Ⅰ)解:取线段EF的中点H,连结
(Ⅰ)解:取线段EF的中点H,连结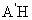 ,因为
,因为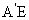 =
=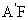 及H是EF的中点,所以
及H是EF的中点,所以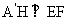 ,
,
又因为平面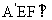 平面
平面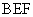 .
.
如图建立空间直角坐标系A-xyz
则 (2,2,
(2,2,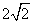 ),C(10,8,0),
),C(10,8,0),
F(4,0,0),D(10,0,0).
故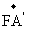 =(-2,2,2
=(-2,2,2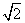 ),
),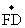 =(6,0,0).
=(6,0,0).
设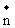 =(x,y,z)为平面
=(x,y,z)为平面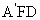 的一个法向量,
的一个法向量,
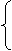 -2x+2y+2
-2x+2y+2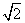 z=0
z=0
所以
6x=0.
取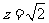 ,则
,则 。
。
又平面 的一个法向量
的一个法向量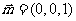 ,
,
故 。
。
所以二面角的余弦值为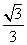
(Ⅱ)解:设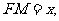 则
则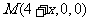 ,
,
因为翻折后,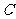 与
与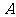 重合,所以
重合,所以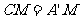 ,
,
故,
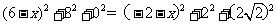 ,得
,得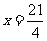 ,
,
经检验,此时点 在线段
在线段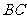 上,
上,
所以 。
。
 方法二:
方法二:
(Ⅰ)解:取线段 的中点
的中点 ,
, 的中点
的中点 ,连结
,连结 。
。
因为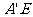 =
=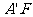 及
及 是
是 的中点,
的中点,
所以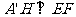
又因为平面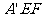
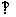 平面
平面 ,
,
所以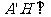 平面
平面 ,
,
又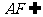 平面
平面 ,
,
故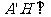
 ,
,
又因为 、
、 是
是 、
、 的中点,
的中点,
易知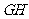 ∥
∥ ,
,
所以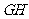
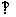
 ,
,
于是
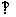 面
面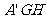 ,
,
所以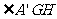 为二面角
为二面角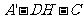 的平面角,
的平面角,
在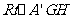 中,
中, =
=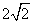 ,
,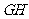 =2,
=2,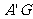 =
=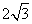
所以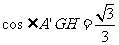 .
.
故二面角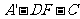 的余弦值为
的余弦值为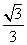 。
。
(Ⅱ)解:设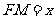 ,
,
因为翻折后,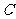 与
与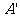 重合,
重合,
所以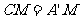 ,
,
而 ,
,
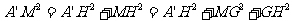
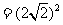
得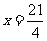 ,
,
经检验,此时点 在线段
在线段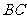 上,
上,
所以 。
。
(2010全国卷2理数)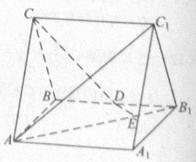 (19)如图,直三棱柱
(19)如图,直三棱柱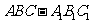 中,
中,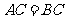 ,
,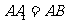 ,
,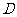 为
为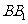 的中点,
的中点,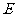 为
为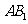 上的一点,
上的一点,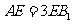 .
.
(Ⅰ)证明: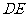 为异面直线
为异面直线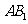 与
与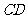 的公垂线;
的公垂线;
 (Ⅱ)设异面直线
(Ⅱ)设异面直线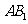 与
与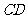 的夹角为45°,求二面角
的夹角为45°,求二面角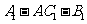 的大小.
的大小.
[命题意图]本试题主要考查空间的线面关系与空间角的求解,考查考生的空间想象与推理计算的能力.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com