
(1) 在等比数列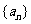 中,
中,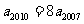 ,则公比q的值为
,则公比q的值为
(A) 2 (B) 3 (C) 4 (D) 8
[答案]A
解析: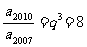
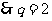
(2) 已知向量a,b满足a·b=0,|a|=1,|b|=2,则|2a-b|=
(A) 0 (B) 2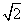 (C) 4 (D) 8
(C) 4 (D) 8
[答案]B
解析:
 .
.
(3) 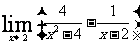 =
=
(A) -1 (B)
-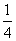 (C)
(C)
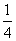 (D) 1
(D) 1
[答案]B
解析: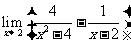 =
=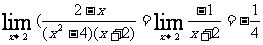
 (4) 设变量x,y满足约束条件
(4) 设变量x,y满足约束条件 ,则z=2x+y的最大值为
,则z=2x+y的最大值为
(A) -2 (B) 4 (C) 6 (D) 8
[答案]C
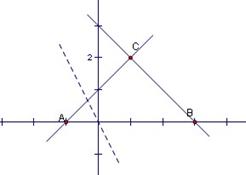
解析:不等式组表示的平面区域如图所示
当直线过点B(3,0)的时候,z取得最大值6.
 (5) 函数
(5) 函数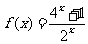 的图象
的图象
(A) 关于原点对称
(B) 关于直线y=x对称
(C) 关于x轴对称
(D) 关于y轴对称
[答案]D
解析: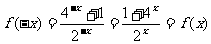
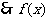 是偶函数,图像关于y轴对称
是偶函数,图像关于y轴对称
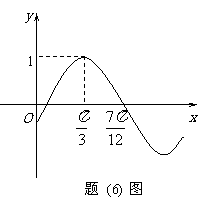
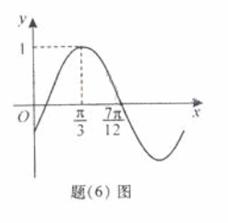
(6) 已知函数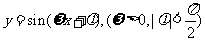 的部分图象如题(6)图所示,则
的部分图象如题(6)图所示,则
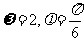 (A)
(A) 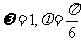 (B)
(B)
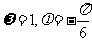
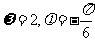
(C) (D)
[答案]D
解析:
由五点作图法知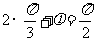 ,
,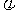 = -
= - .
.
(7) 已知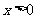 ,
,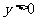 ,
, ,则
,则 的最小值是
的最小值是
(A) 3 (B)
4 (C)
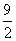 (D)
(D)
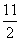
[答案]B
解析:考察均值不等式
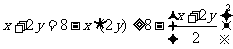 ,整理得
,整理得
即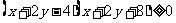 ,又
,又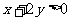 ,
,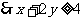
(8) 直线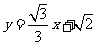 与圆心为D的圆
与圆心为D的圆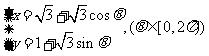 交于A、B两点,则直线AD与BD的倾斜角之和为
交于A、B两点,则直线AD与BD的倾斜角之和为
(A) 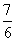 π (B)
π (B)
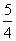 π (C)
π (C)
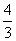 π (D)
π (D)
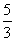 π
π
[答案]C
解析:数形结合
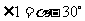
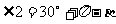
由圆的性质可知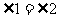
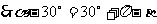
故
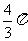
(9) 某单位安排7位员工在10月1日至7日值班,每天安排1人,每人值班1天,若7位员工中的甲、乙排在相邻两天,丙不排在10月1日,丁不排在10月7日,则不同的安排方案共有
(A) 504种 (B) 960种 (C) 1008种 (D) 1108种
[答案]C
解析:分两类:甲乙排1、2号或6、7号 共有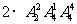 种方法
种方法
甲乙排中间,丙排7号或不排7号,共有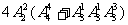 种方法
种方法
故共有1008种不同的排法
(10) 到两互相垂直的异面的距离相等的点,在过其中一条直线且平行于另一条直线的平面内的轨迹是
(A) 直线 (B) 椭圆 (C) 抛物线 (D) 双曲线
[答案]D
解析:排除法 轨迹是轴对称图形,排除A、C,轨迹与已知直线不能有交点,排除B
20.已知a,b是不全为零的实数, ,
,
(1) 当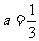 ,存在
,存在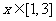 ,使f(x)>0,求b范围;
,使f(x)>0,求b范围;
(2) 求证: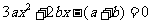 在区间(0,1)内至少有一个实根.
江苏省新海高级中学2009-2010学年度第二学期期中考试
在区间(0,1)内至少有一个实根.
江苏省新海高级中学2009-2010学年度第二学期期中考试
19.某地建一座桥,两端的桥墩已建好,这两墩相距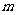 米,余下工程只需要建两端桥墩之间的桥面和桥墩,经预测,一个桥墩的工程费用为256万元,距离为
米,余下工程只需要建两端桥墩之间的桥面和桥墩,经预测,一个桥墩的工程费用为256万元,距离为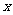 米的相邻两墩之间的桥面工程费用为
米的相邻两墩之间的桥面工程费用为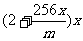 万元。假设桥墩等距离分布,所有桥墩都视为点,且不考虑其他因素,记余下工程的费用为
万元。假设桥墩等距离分布,所有桥墩都视为点,且不考虑其他因素,记余下工程的费用为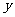 万元.
万元.
(Ⅰ)试写出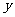 关于
关于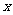 的函数关系式;
的函数关系式;
(Ⅱ)当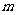 =625米时,需新建多少个桥墩才能使
=625米时,需新建多少个桥墩才能使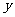 最小?
最小?
18.设命题P:关于x的不等式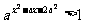 (a>0且a≠1)的解集为{x|-a<x<2a};命题Q:y=lg(ax2-x+a)的定义域为R。如果P或Q为真,P且Q为假,求a的取值范围.
(a>0且a≠1)的解集为{x|-a<x<2a};命题Q:y=lg(ax2-x+a)的定义域为R。如果P或Q为真,P且Q为假,求a的取值范围.
17.(1)数列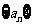 是等差数列,前n项和
是等差数列,前n项和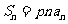 ,(
,(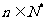 ,
,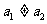 )
)
求证:常数p=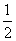 ;
;
(2)已知等差数列a,b,c中的三个数都是正数,且公差不等于零,求证:它们的倒数所组成的数列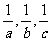 不可能成等差数列.
不可能成等差数列.
16.若复数z满足: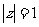
(1) 求 的取值范围;
的取值范围;
(2) 若z+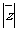 =a+
=a+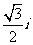 ,求实数a的值.
,求实数a的值.
15.设集合A=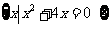 ,B=
,B=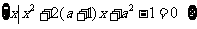
(1) 求A;
(2) 若B=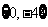 ,求实数a的值.
,求实数a的值.
14.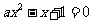 在区间
在区间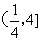 内有解,求实数a范围为
.
内有解,求实数a范围为
.
13.若复数z满足 ,则
,则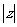 最小值为 .
最小值为 .
12.观察下列等式:
1=1 13=1
1+2=3 13+23=9
1+2+3=6 13+23+33=36
1+2+3+4=10 13+23+33+43=100
1+2+3+4+5=15 13+23+33+43+53=225
可以推测:13+23+33+…+n3=________(n∈N*,用含有n的代数式表示).
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com