
20. There are many people downstairs. What do you think ______?
A. to happen B. happening C. is happened D. has happened
19. ______ we deal with our problems, we can easily become unhappy.
A. Unless B. Until C. Though D. Whether
18. Alice had a wonderful time yesterday, ______?
A. hadn’t she B. wasn’t she C. didn’t she D. wouldn’t she
17. - Is tea ready?
- No, mother is ______ it ready now.
A. doing B. cooking C. burning D. getting
从A、B、C、D四个选项中,选出可以填入空白处的最佳选项。
16. The underlined part in the word “lived” is pronounced as ______.
A. ∕t∕ B. ∕d∕ C. ∕Id∕ D. ∕It∕
(16) (本小题满分13分,(Ⅰ)小问7分,(Ⅱ)小问6分.)
设函数 .
.
(Ⅰ)
求 的值域;
的值域;
(Ⅱ)
记△ABC的内角A、B、C的对边长分别为a、b、c,若 ,
, ,
, ,求a的值.
,求a的值.

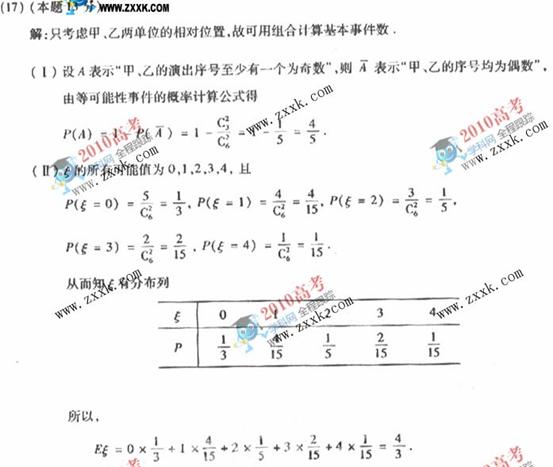
(17) (本小题满分13分,(Ⅰ)小问5分,(Ⅱ)小问8分.)
在甲、乙等6个单位参加的一次“唱读传讲”赛出活动中,每个单位的节目集中安排在一起.若采用抽签的方式随机确定各单位的演出顺序(序号为1,2,…,6),求:
(Ⅰ) 甲、乙两单位的演出序号至少有一个为奇数的概率;
(Ⅱ) 甲、乙两单位之间的演出单位个数ξ的分布列与期望.
(18) (本小题满分13分,(Ⅰ)小问5分,(Ⅱ)小问8分.)
已知函数 ,其中实数
,其中实数
(Ⅰ)
若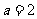 ,求曲线
,求曲线 在点
在点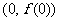 处的切线方程;
处的切线方程;
(Ⅱ)
若 在
在 处取得极值,试讨论
处取得极值,试讨论 的单调性.
的单调性.

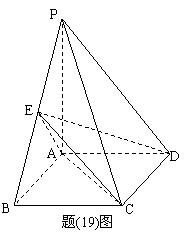 (19) (本小题满分12分,(Ⅰ)小问5分,(Ⅱ)小问7分.)
(19) (本小题满分12分,(Ⅰ)小问5分,(Ⅱ)小问7分.)
如题(19)图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥底面ABCD,PA=AB= ,点E是棱PB的中点.
,点E是棱PB的中点.
(Ⅰ) 求直线AD与平面PBC的距离;
(Ⅱ)
若AD=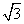 ,求二面角A-EC-D的平面角的余弦值.
,求二面角A-EC-D的平面角的余弦值.





(20) (本小题满分12分,(Ⅰ)小问5分,(Ⅱ)小问7分.)
已知以原点O为中心,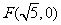 为右焦点的双曲线C的离心率
为右焦点的双曲线C的离心率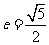 .
.
(Ⅰ)求双曲线C的标准方程及其渐近线方程;
(Ⅱ)如题(20)图,已知过点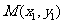 的直线
的直线 :
: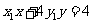 与过点
与过点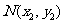 (其中
(其中 )的直线
)的直线 :
: 的交点E在双曲线C上,直线MN与双曲线的两条渐近线分别交于G、H两点,求△OGH的面积.
的交点E在双曲线C上,直线MN与双曲线的两条渐近线分别交于G、H两点,求△OGH的面积.




(21) (本小题满分12分,(Ⅰ)小问5分,(Ⅱ)小问7分.)
在数列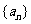 中,
中,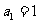 ,
,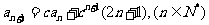 其中实数
其中实数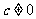 .
.
(Ⅰ)
求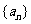 的通项公式;
的通项公式;
(Ⅱ)
若对一切 有
有 ,求c的取值范围.
,求c的取值范围.


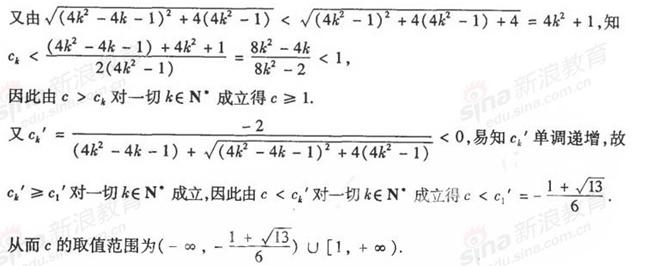

(11) 已知复数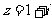 ,则
,则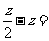 ____________.
____________.
[答案]-2i
解析: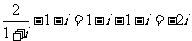
(12) 设 ,
,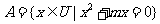 ,若C
,若C ,则实数
,则实数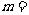 ________.
________.
[答案]-3
解析:
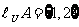 ,
,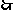 A={0,3},故m= -3
A={0,3},故m= -3
(13) 某篮球队员在比赛中每次罚球的命中率相同,且在两次罚球中至少命中一次的概率为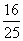 ,则该队员每次罚球的命中率为____________.
,则该队员每次罚球的命中率为____________.
[答案]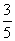
解析:由 得
得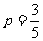
(14) 已知以F为焦点的抛物线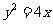 上的两点A、B满足
上的两点A、B满足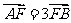 ,则弦AB的中点到准线的距离为____________.
,则弦AB的中点到准线的距离为____________.
 [答案]
[答案]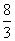
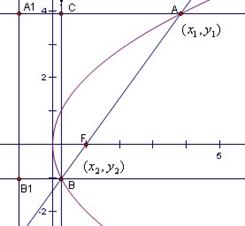
解析:设BF=m,由抛物线的定义知
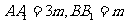
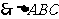 中,AC=2m,AB=4m,
中,AC=2m,AB=4m,
直线AB方程为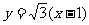
与抛物线方程联立消y得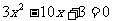
所以AB中点到准线距离为
(15) 已知函数 满足:
满足: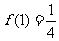 ,
,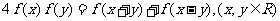 ,则
,则 ____________.
____________.
[答案]
解析:取x=1 y=0得
法一:通过计算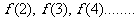 ,寻得周期为6
,寻得周期为6
法二:取x=n y=1,有f(n)=f(n+1)+f(n-1),同理f(n+1)=f(n+2)+f(n)
联立得f(n+2)= —f(n-1) 所以T=6 故 =f(0)=
=f(0)= 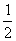 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com