
5.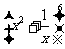 的展开式中常数项是
(用数字作答).
的展开式中常数项是
(用数字作答).
4.若复数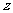 满足
满足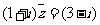 ,则
,则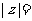 .
.
3.复数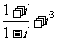 的值是___________________.
的值是___________________.
2.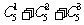 的值为___________________.
的值为___________________.
1.复数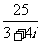 的虚部为___________________.
的虚部为___________________.
6.
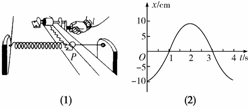
图1-1-18
简谐运动的振动图线可用下述方法画出:如图1-1-18(1)所示,在弹簧振子的小球上安装一枝绘图笔P,让一条纸带在与小球振动方向垂直的方向上匀速运动,笔P在纸带上画出的就是小球的振动图象.取振子水平向右的方向为振子离开平衡位置的位移正方向,纸带运动的距离代表时间,得到的振动图线如图1-1-18(2)所示.
(1)为什么必须匀速拖动纸带?
(2)刚开始计时时,振子处在什么位置?t=17 s时振子相对平衡位置的位移是多少?
(3)若纸带运动的速度为2 cm/s,振动图线上1、3两点间的距离是多少?
(4)振子在______ s末负方向速度最大;在______ s末正方向加速度最大;2.5 s时振子正在向______方向运动.
(5)写出振子的振动方程.
解析:(1)纸带匀速运动时,由x=vt知,位移与时间成正比,因此在匀速条件下,可以用纸带通过的位移表示时间.
(2)由图(2)可知t=0时,振子在平衡位置左侧最大位移处;周期T=4 s,t=17 s时位移为零.
(3)由x=vt,所以1、3间距x=2 cm/s×2 s=4 cm.
(4)3 s末负方向速度最大;加速度方向总是指向平衡位置,所以t=0或t=4 s时正方向加速度最大;t=2.5 s时,向-x方向运动.
(5)x=10sin cm
答案:(1)在匀速条件下,可以用纸带通过的位移表示时间
(2)左侧最大位移 零 (3)4 cm (4)3 0或4 -x (5)x=10sin cm
5.
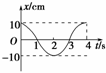
图1-1-17
根据如图1-1-17所示的振动图象:
(1)算出下列时刻振子对平衡位置的位移.
①t1=0.5 s;②t2=1.5 s
(2)将位移随时间的变化规律写成x=Asin(ωt+φ)的形式并指出振动的初相位是多少?
解析:(1)由图象可知A=10 cm,T=4 s
故位移:x=Acos ωt=10cos t=10cos t cm
①当t1=0.5 s时,x1=5 cm
②当t2=1.5 s时,x2=-5 cm
(2)振子的位移表达式为:x=10cos t=10sincm,初相位为:φ=.
答案:(1)①5 cm ②-5 cm (2)x=10sincm
4.
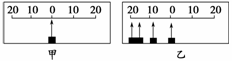
图1-1-16
(2010·朝阳区模拟)如图1-1-16所示为用频闪照相的方法拍到的一个水平放置的弹簧振子振动情况.甲图是振子静止在平衡位置的照片,乙图是振子被拉伸到左侧距平衡位置20 mm处,放手后向右运动周期内的频闪照片.已知频闪的频率为10 Hz.求:
(1)相邻两次闪光的时间间隔t0、振动的周期T0.
(2)若振子的质量为20 g,弹簧的劲度系数为50 N/m,则振子的最大加速度是多少?
解析:(1)T==0.1 s,即相邻两次闪光的时间间隔为t0=0.1 s.振子从最大位移处运动到平衡位置经历时间为0.3 s,故振子振动周期T0=1.2 s.
(2)am===50 m/s2
答案:(1)0.1 s 1.2 s (2)50 m/s2
3.
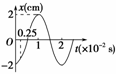
图1-1-15
一质点做简谐运动,其位移和时间关系如图1-1-15所示.
(1)求t=0.25×10-2 s时的位移;
(2)在t=1.5×10-2 s到2×10-2 s的振动过程中,质点的位移、回复力、速度、动能、势能如何变化?
(3)在t=0至8.5×10-2 s时间内,质点的路程、位移各多大?
解析:(1)由图可知A=2 cm,T=2×10-2 s,
振动方程为x=Asin=-Acos ωt=-2cos t cm=-2cos(102πt) cm
当t=0.25×10-2 s时x=-2cos cm=- cm.
(2)由图可知在1.5×10-2 s-2×10-2 s内,质点的位移变大,回复力变大,速度变小,动能变小,势能变大.
(3)从t=0至8.5×10-2 s的时间内质点的路程为s=17A=34 cm,位移为2 cm.
答案:(1)- cm (2)位移变大,回复力变大,速度变小,动能变小,势能变大 (3)34 cm 2 cm
2.
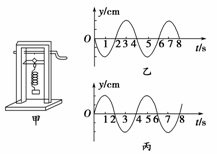
图1-1-14
一砝码和一轻弹簧构成弹簧振子,如图1-1-14甲所示,该装置可用于研究弹簧振子的受迫振动.匀速转动把手时,曲杆给弹簧振子驱动力,使振子做受迫振动.把手匀速转动的周期就是驱动力的周期,改变把手匀速转动的速度就可以改变驱动力的周期.若保持把手不动,给砝码一向下的初速度,砝码便做简谐运动,振动图线如图1-1-14乙所示.当把手以某一速度匀速转动,受迫振动达到稳定时,砝码的振动图象如图1-1-14丙所示.若用T0表示弹簧振子的固有周期,T表示驱动力的周期,Y表示受迫振动达到稳定后砝码振动的振幅,则
(1)稳定后,物体振动的频率f=________ Hz.
(2)欲使物体的振动能量最大,需满足什么条件?
答:________________________________________________________________________.
(3)利用上述所涉及的知识,请分析某同学所提问题的物理道理.
“某同学考虑,我国火车第六次大提速时,需尽可能的增加铁轨单节长度,或者是铁轨无结头”.
答:________________________________________________________________________.
解析:(1)由丙图可知,f== Hz=0.25 Hz.
(2)物体振动能量最大时,即振幅最大,故应发生共振,所以应有T=T0=4 s.
(3)若单节车轨非常长,或无结头,则驱动力周期非常大,从而远离火车的固有周期,即火车的振幅较小.以便来提高火车的车速.
答案:(1)0.25 (2)T=T0=4 s
(3)远离火车的固有周期,以便于提高火车的车速
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com