
(1)
设 则
则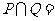
(A) (B)
(B)
(C)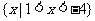 (D)
(D)
解析: ,故答案选D,本题主要考察了集合的基本运算,属容易题
,故答案选D,本题主要考察了集合的基本运算,属容易题
(2)
 已知函数
已知函数  若
若
 =
=
(A)0 (B)1 (C)2 (D)3
解析: +1=2,故
+1=2,故 =1,选B,本题主要考察了对数函数概念及其运算性质,属容易题
=1,选B,本题主要考察了对数函数概念及其运算性质,属容易题
(3)
设i为虚数单位,则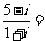
(A)-2-3i (B)-2+3i
(C)2-3i (D)2+3i
解析:选C,本题主要考察了复数代数形式的四则运算,属容易题
(4) 某程序框图所示,若输出的S=57,则判断框内为
(A) k>4? (B) k>5?
(C) k>6? (D) k>7?
解析:选A,本题主要考察了程序框图的结构,以及与数列有关的简单运算,属容易题
(5)设 为等比数列
为等比数列 的前n项和,
的前n项和,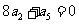 则
则
(A)-11 (B)-8
(C)5 (D)11
解析:通过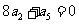 ,设公比为
,设公比为 ,将该式转化为
,将该式转化为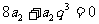 ,解得
,解得 =-2,带入所求式可知答案选A,本题主要考察了本题主要考察了等比数列的通项公式与前n项和公式
=-2,带入所求式可知答案选A,本题主要考察了本题主要考察了等比数列的通项公式与前n项和公式
(6)设0<x< ,则“x sin2x<1”是“x sinx<1”的
,则“x sin2x<1”是“x sinx<1”的
(A)充分而不必要条件 (B)必要而不充分条件
(C)充分必要条件 (D)既不充分也不必要条件
解析:因为0<x< ,所以sinx<1,故xsin2x<xsinx,结合xsin2x与xsinx的取值范围相同,可知答案选B,本题主要考察了必要条件、充分条件与充要条件的意义,以及转化思想和处理不等关系的能力,属中档题
,所以sinx<1,故xsin2x<xsinx,结合xsin2x与xsinx的取值范围相同,可知答案选B,本题主要考察了必要条件、充分条件与充要条件的意义,以及转化思想和处理不等关系的能力,属中档题
 x+3y-3≥0,
x+3y-3≥0,
(7)若实数x,y满足不等式组合 2x-y-3≤0,则x+y的最大值为
x-y+1≥0,
(A)9 (B)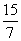
 (C)1
(D)
(C)1
(D)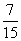
解析:将最大值转化为y轴上的截距,可知答案选A,本题主要考察了用平面区域二元一次不等式组,以及简单的转化思想和数形结合的思想,属中档题
(8)若某几何体的三视图(单位:cm)如图所示,则此几何体的体积是
(A) cm3
(B)
cm3
(B)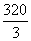 cm3
cm3
(C) cm3
(D)
cm3
(D) cm3
cm3
解析:选B,本题主要考察了对三视图所表达示的空间几何体的识别以及几何体体积的计算,属容易题
(9)已知x是函数f(x)=2x+ 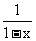 的一个零点.若
的一个零点.若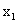 ∈(1,
∈(1,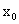 ),
),
 ∈(
∈(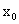 ,+
,+ ),则
),则
(A)f(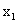 )<0,f(
)<0,f( )<0 (B)f(
)<0 (B)f(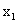 )<0,f(
)<0,f( )>0
)>0
(C)f(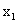 )>0,f(
)>0,f( )<0 (D)f(
)<0 (D)f(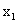 )>0,f(
)>0,f( )>0
)>0
解析:选B,考察了数形结合的思想,以及函数零点的概念和零点的判断,属中档题
(10)设O为坐标原点, ,
, 是双曲线
是双曲线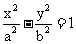 (a>0,b>0)的焦点,若在双曲线上存在点P,满足∠
(a>0,b>0)的焦点,若在双曲线上存在点P,满足∠ P
P =60°,∣OP∣=
=60°,∣OP∣= ,则该双曲线的渐近线方程为
,则该双曲线的渐近线方程为
(A)x± y=0
(B)
y=0
(B) x±y=0
x±y=0
(C)x± =0
(D)
=0
(D) ±y=0
±y=0
解析:选D,本题将解析几何与三角知识相结合,主要考察了双曲线的定义、标准方程,几何图形、几何性质、渐近线方程,以及斜三角形的解法,属中档题
非选择题部分(共100分)
二,填空题:本大题共7小题,每小题4分,共28分。
(11)在如图所示的茎叶图中,甲、乙两组数据的中位数分别是 、

解析:45;46,本题主要考察了茎叶图所表达的含义,以及从样本数据中提取数字特征的能力,属容易题。
(12)函数 的最小正周期是
。
的最小正周期是
。
解析:对解析式进行降幂扩角,转化为 ,可知其最小正周期为
,可知其最小正周期为 ,本题主要考察了二倍角余弦公式的灵活运用,属容易题。
,本题主要考察了二倍角余弦公式的灵活运用,属容易题。
(13)已知平面向量 则
则 的值是 。
的值是 。
解析: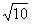 ,由题意可知
,由题意可知 ,结合
,结合 ,解得
,解得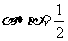 ,所以
,所以 2=
2= ,开方可知答案为
,开方可知答案为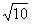 ,本题主要考察了平面向量的四则运算及其几何意义,属中档题。
,本题主要考察了平面向量的四则运算及其几何意义,属中档题。
(14)在如下数表中,已知每行、每列中的树都成等差数列,
那么,位于下表中的第n行第n+1列的数是 。

解析:第n行第一列的数为n,观察得,第n行的公差为n,所以第n0行的通项公式为

 ,又因为为第n+1列,故可得答案为
,又因为为第n+1列,故可得答案为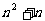 ,本题主要考察了等差数列的概念和通项公式,以及运用等差关系解决问题的能力,属中档题
,本题主要考察了等差数列的概念和通项公式,以及运用等差关系解决问题的能力,属中档题
(15)若正实数X,Y 满足2X+Y+6=XY , 则XY 的最小值是 。
解析:运用基本不等式, ,令
,令 ,可得
,可得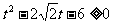 ,注意到t>0,解得t≥
,注意到t>0,解得t≥ ,故xy的最小值为18,本题主要考察了用基本不等式解决最值问题的能力 ,以及换元思想和简单一元二次不等式的解法,属中档题
,故xy的最小值为18,本题主要考察了用基本不等式解决最值问题的能力 ,以及换元思想和简单一元二次不等式的解法,属中档题
(16) 某商家一月份至五月份累计销售额达3860万元,预测六月份销售额为500万元,七月份销售额比六月份递增x%,八月份销售额比七月份递增x%,九、十月份销售总额与七、八月份销售总额相等,若一月至十月份销售总额至少至少达7000万元,则,x 的最小值 。
解析:20;本题主要考察了用一元二次不等式解决实际问题的能力,属中档题
(17)在平行四边形ABCD中,O是AC与BD的交点,P、Q、M、N分别是线段OA、OB、OC、OD的中点,在APMC中任取一点记为E,在B、Q、N、D中任取一点记为F,设G为满足向量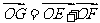 的点,则在上述的点G组成的集合中的点,落在平行四边形ABCD外(不含边界)的概率为 。
的点,则在上述的点G组成的集合中的点,落在平行四边形ABCD外(不含边界)的概率为 。

解析:由题意知,G点共有16种取法,而只有E为P、M中一点,F为Q、N中一点时,落在平行四边形内,故符合要求的G的只有4个,因此概率为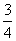 ,本题主要考察了平面向量与古典概型的综合运用,属中档题
,本题主要考察了平面向量与古典概型的综合运用,属中档题
24.(本小题满分16分)
已知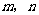 为正整数,
为正整数,
(1)证明:当 时,
时, ;
;
(2)对于 ,已知
,已知 求证:
求证: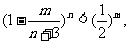
 ;
;
(3)求出满足等式 的所有正整数
的所有正整数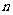 .
.
江苏省新海高级中学2009-2010学年度第二学期期中考试
23.(本小题满分16分)
袋子中装着标有数字1,2,3,4,5的小球各2个,从袋子中任取3个小球,每个小球被取出的可能性都相等,用 表示取出的3个小球中的最大数字,求:
表示取出的3个小球中的最大数字,求:
(1)取出的3个小球上的数字互不相同的概率;
(2)随机变量 的概率分布;
的概率分布;
(3)设“函数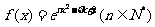 在区间
在区间 上单调递增”为事件
上单调递增”为事件 ,求事件
,求事件 发生的概率.
发生的概率.
22.(本小题满分16分)
在 的展开式中,已知第
的展开式中,已知第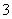 项与第
项与第 项的系数相等.
项的系数相等.
(1)求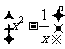 展开式中的系数最大的项和系数最小的项;
展开式中的系数最大的项和系数最小的项;
(2)求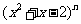 展开式中含
展开式中含 项的系数.
项的系数.
21. (本小题满分15分)
数列 满足
满足 (n∈N*).
(n∈N*).
(1)计算 ,并由此猜想通项公式
,并由此猜想通项公式 ;
;
(2)用数学归纳法证明(1)中的猜想.
20. (本小题满分15分)
 如图,已知三棱锥
如图,已知三棱锥 的侧棱
的侧棱 两两垂直,且
两两垂直,且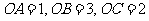 ,
, 是
是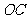 的中点.
的中点.
(1)求异面直线 与
与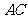 所成角的余弦值;
所成角的余弦值;
(2)求二面角 的余弦值.
的余弦值.
19. (本小题满分14分)
通过计算可得下列等式:
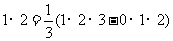

…………
 (
( )
)
将以上各式分别相加得:
即:
类比上述求法:请你求出 的值. (
的值. ( )
)
18. (本小题满分14分)
设随机变量 的概率分布列为
的概率分布列为 试求:
试求:
(1)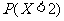 ;(2)
;(2) 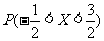 ;(3)
;(3) .
.
17. (本小题满分14分)
已知复数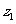 满足
满足 ,
, 其中
其中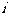 为虚数单位,
为虚数单位, ,若
,若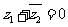 ,求实数
,求实数 的值.
的值.
16.已知数列 满足
满足 ,
,  ,
,
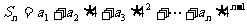 ,类比课本中推导等比数列前
,类比课本中推导等比数列前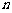 项和公式的方法,可求得
项和公式的方法,可求得 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com