
21.已知各项都不为零的数列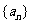 的前
的前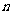 项和是
项和是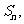 且
且
令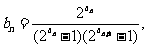 数列
数列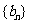 的前
的前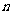 项和是
项和是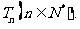
(1)求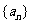 的通项公式
的通项公式
(2)求证: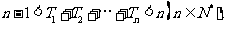
20.已知椭圆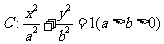 的离心率为
的离心率为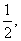 且椭圆
且椭圆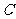 的中心关于直线
的中心关于直线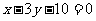 的对称点在椭圆
的对称点在椭圆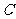 的右准线上.
的右准线上.
(1)求椭圆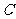 的方程;
的方程;
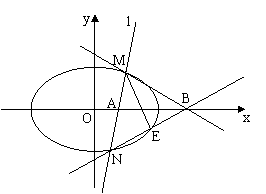 (2)设点
(2)设点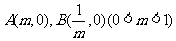 是
是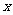 轴上的两点,过点
轴上的两点,过点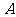 作斜率不为0的直线与椭圆
作斜率不为0的直线与椭圆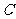 交于
交于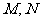 两点,作直线
两点,作直线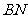 交椭圆
交椭圆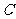 于另一点
于另一点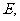 证明
证明 是等腰三角形.
是等腰三角形.
19.(理)设函数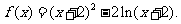
(1)求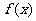 的单调区间;
的单调区间;
(2)若关于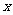 的方程
的方程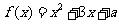 在区间
在区间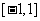 上唯一实根,求实数
上唯一实根,求实数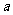 的取值范围.
的取值范围.
(文)已知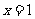 是函数
是函数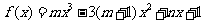 的一个极值点,
的一个极值点,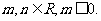
(1)求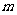 与
与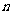 的关系表达式; (2)求
的关系表达式; (2)求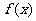 的单调区间;
的单调区间;
(3)当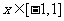 时,函数
时,函数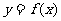 的图象上任意一点处的切线的斜率恒大于
的图象上任意一点处的切线的斜率恒大于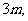 求
求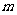 的取值范围.
的取值范围.
18.2008年全球金融动荡,一房地产商为资金保值,决定购买盒装金砖,按照包装标识每盒中装有10块形状、质量完全相同的金砖,但是由于经验不足,房地产商购置的每盒金砖中都有一块质量略轻于其余金砖的“次品”,为了找出这块“次品”,设计了两种方案:
方案甲:将10块金砖平均分成五组,把每组中的两块金砖分别放在天平的两端称量,逐组进行,直到找出“次品”为止(天平低的一端为“次品”金砖).
方案乙:将10块金砖分成3块、3块、4块三组,先把两组3块的金砖放在天平上称量,若天平不平,再在较轻的一组中任取两块称量即可;若天平平衡,则在4块的这组中任取两块进行称量,直到找到“次品”为止,令“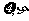 ”分别为方案甲、乙找到“次品”金砖所需的称量次数.
”分别为方案甲、乙找到“次品”金砖所需的称量次数.
(理)(1)写出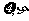 的分布列及期望; (2)求
的分布列及期望; (2)求
(文)(1)使用两个方案找出次品所需的最少称量次数是多少,并求出用最少称量次数找出次品的概率; (2)求
17.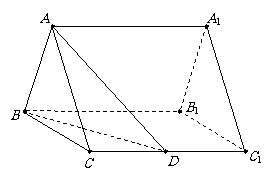 如图,已知正三棱柱
如图,已知正三棱柱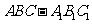 的底面边长是2,
的底面边长是2,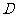 是
是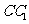 的中点,直线
的中点,直线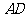 与侧面
与侧面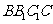 所成的角是45°.
所成的角是45°.
(1)求二面角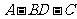 的大小;
的大小;
(2)求点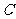 到平面
到平面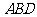 的距离.
的距离.
16.已知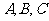 是
是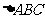 的内角,向量
的内角,向量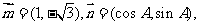 且
且
(1)求角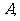 (2)若
(2)若 求
求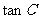 的值.
的值.
15.右图给出一个图表,它有这样的规律:表中第一行只有
一个数1,表中第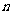 行
行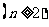 有
有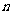 个数,且两端的数都是
个数,且两端的数都是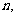
其余的每一个数都等于它肩上两个数的和,则第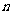 行的第2
行的第2
个数是____________.
13.过球一半径的中点作垂直于此半径的球的截面,则此截面面积与球表面积之比为____________.
|
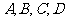 四位同学准备从三门选修课中各选一门,若要求每门选修课至少有一人选修,且
四位同学准备从三门选修课中各选一门,若要求每门选修课至少有一人选修,且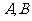 不选修同一门课,则不同的选法有_________种(用数字表示).
不选修同一门课,则不同的选法有_________种(用数字表示).12.(理)已知数列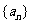 满足
满足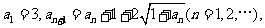 则
则
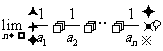 ______________.
______________.
(文)函数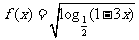 的定义域为________________.
的定义域为________________.
11.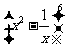 的展开式中,常数项等于________________.
的展开式中,常数项等于________________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com