
2. 若 为圆
为圆 的弦
的弦 的中点,则直线
的中点,则直线 的方程为
的方程为
A.  B.
B. C.
C. D.
D.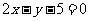
1. 若集合 ,则
,则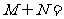
A.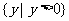 B.
B.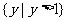 C.
C. 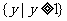 D.
D.
22.(本小题满分12分)
已知双曲线x2-2y2=2的左、右焦点分别是F1、F2,动点P满足{PF1}+{PF2}=4.
(1) 求动点P的轨迹E的过程。
(2) 设过点F2且不垂直与坐标轴的动直线a交轨迹E与A、B两点,试问在y轴上是否存在一点D使得以DA、DB为邻边的平行四边形为菱形?若存在,试判断点D的活动范围:若不存在,试说明理由。
21.(本小题满分12分)
数列{ an }中, a1=t, a2=t2,(t≠1).x=是函数
f(x)= an-1x3-3[(t+1) an- an+1]x+1(n≥2)的一个极值点。
(1)证明数列[an-1- an]是等比数列,并求数列{an}的通项公式;
(2)记bn=2(1-), 当t=2时,数列{bn}的前n项和为Sn,求使Sn>2010的n的最小值。
20.(本小题满分12分)
已知函数f(x)=x3+ax2+bx+c,在x= - 与x=1时都取得极值。
求:(1)求a、b的值
(2)若对x∈ [ -1 ,2 ], 有f(x)<c2恒成立,求c的取值范围。
19.(本小题满分12分)
如图所示,四棱锥P-ABCD的底面是一个矩形,AB=3.AD=1.又PA⊥ AB,PA=4,
∠PAD=60°.
求:(1) 四棱锥P-ABCD的体积。
 (2) 二面角P - BC - D的正切值.
(2) 二面角P - BC - D的正切值.
18. (本小题满分12分)
在环保知识有奖问答比赛中,甲、乙、丙同时回答一道有关水体净化知识的问题,甲答对的概率是,甲、丙两人都打错的概率是,乙、丙两人都答对的概率是.
求:(1)乙、丙两人各自答对这道题目的概率。
(2)甲、乙、丙三人中至少有两人答对这道题目的概率。
17.(本小题满分10分)
已知a、b是不共线的向量,且a=(5cosα,5sinα), b=(5cosβ, 5sinβ)
(1) 求证:a+b与a-b垂直。
(2) 若{a+b}= ,求cos(α-β)
16.已知长方形ABCD的一组邻边长分别为3、4,沿对角线AC折成一个三菱锥,若记二面角B-AC-D的大小为θ( 0<θ<) ,则该三菱锥的外接球的体积为 .
15.在实数的原有运算中,我们补充运算“*”如下:当a≥b时,a*b=a; 当a<b时, a*b=b2.设函数f(x)=(1*x)x - (2*x), x ∈ [ -2,2 ],则函数f(x)的值域为 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com