
20.(本小题满分12分)
已知数列{an}的前n项和为Sn,若a1=3,点(Sn,Sn+1)在直线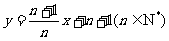 上.
上.
|
 是等差数列;
是等差数列;
(Ⅱ)若数列{bn}满足bn=an·2 ,求数列{bn}的前n项和Tn;
(Ⅲ)设Cn=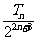 ,求证:C1+ C2+…+Cn>
,求证:C1+ C2+…+Cn> .
.
19.(本小题满分12分)
如图所示,在矩形ABCD中,AB =4,AD =2, E是CD的中点,O 为AE的中点,F是AB 的中点.以AE为折痕将△ADE向上折起,使面DAE⊥面ABCE.
(Ⅰ)求证:OF∥面BDE;
(Ⅱ)求证:AD⊥面BDE;
(Ⅲ)求三棱锥D-BCE的体积.

18.(本小题满分12分)
班级联欢时,主持人拟出了如下一些节目:跳双人舞、独唱、朗诵等,指定3个男生和2个女生来参与,把5个人分别编号为1,2,3,4,5,其中1,2,3号是男生,4,5号是女生,将每个人的号分别写在5张相同的卡片上,并放入一个箱子中充分混合,每次从中随即地取出一张卡片,取出谁的编号谁就参与表演节目.
(Ⅰ)为了选出2人来表演双人舞,连续抽取2张卡片,求取出的2人不全是男生的概率;
(Ⅱ)为了选出2人分别表演独唱和朗诵,抽取并观察第一张卡片后,又放回箱子中,充分混合后再从中抽取第二张卡片,求:独唱和朗诵由同一个人表演的概率.
17.(本小题12分)
已知函数 =Asin(ωx+φ)( A>0, ω>0,
=Asin(ωx+φ)( A>0, ω>0, <
<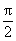 =的图像与y轴的交点为(0,1),它在y轴右侧的第一个最高点和第一个最低点的坐标分别为(x0,2)和(x0+2π,-2).
=的图像与y轴的交点为(0,1),它在y轴右侧的第一个最高点和第一个最低点的坐标分别为(x0,2)和(x0+2π,-2).
(Ⅰ)求 的解析式及x0的值;
的解析式及x0的值;
(Ⅱ)若锐角θ满足cosθ= ,求f(4θ)的值.
,求f(4θ)的值.

16.对于命题:如果O是线段AB上一点,则│ │·
│·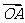 +│
+│ │·
│· =
= ;将它类比到平面的情形是:若O是△ABC内一点,有S△OBC·
;将它类比到平面的情形是:若O是△ABC内一点,有S△OBC· +S△OCA·
+S△OCA· +S△OBA·
+S△OBA· =
= ;将它类比到空间的情形应该是:若O是四面体ABCD内一点,则有
.
;将它类比到空间的情形应该是:若O是四面体ABCD内一点,则有
.
15.今年一轮又一轮的寒潮席卷全国.某商场为了了解某品牌羽绒服的月销售量y(件)与月平均气温x(℃)之间的关系,随机统计了某4个月的月销售量与当月平均气温,数据如下表:
|
月平均气温x(℃) |
17 |
13 |
8 |
2 |
|
月销售量y(件) |
24 |
33 |
40 |
55 |
由表中数据算出线性回归方程 中的b≈-2.气象部门预测下个月的平均气温约为6℃,据此估计,该商场下个月毛衣的销售量的件数约为
.
中的b≈-2.气象部门预测下个月的平均气温约为6℃,据此估计,该商场下个月毛衣的销售量的件数约为
.
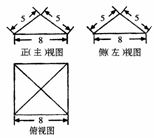
14.一个几何体的三视图如图所示,那么此几何体的侧面积(单位:cm2)为 .
13.已知函数f(x)= 若f(x)在(-∞,+∞)上单调递增,则实数a的
取值范围为 .
12.已知P为抛物线y2=4x上一个动点,Q为圆 上一个动点,那么点P到
上一个动点,那么点P到
点Q的距离与点P到抛物线的准线距离之和的最小值是 ( )
A. B.
B.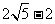 C.
C. D.
D.
第Ⅱ卷(非选择题90分)
11.若实数x,y满足不等式组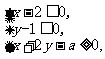 ,目标函数t=x-2y的最大值为2,则实数a的值是
,目标函数t=x-2y的最大值为2,则实数a的值是
( )
A.-2 B.0 C.1 D.2
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com