
4、2004年:《戍妇歌》
作者:不详
作者自述:这是2004年高考全国卷Ⅱ的考试作文,作文要求以“遭遇挫折和放大痛苦”为话题,自定立意,自选文体,自拟标题。我在贵州省织金县参加了这一届的高考,以这篇“古诗体”的诗歌《戍妇歌》获得满分。本人从小就对旧体诗词有着浓厚的兴趣,一直以来坚持学习并且尝试着进行创作,至今写过百余首不同体裁、风格的旧体诗词作品。鉴于对传统文化的热爱,且希冀与志同道合的人把我们的传统文化继承和发扬下去,在此,谨把这首有幸获得高考满分的“古诗体”作品《戍妇歌》录下来与大家分享。
(注:这首《戍妇歌》采用了五言古诗的风格,类似于《孔雀东南飞》的叙事形式,以一个丈夫被征召从军的“戍妇”的口吻,讲述了一段被封建战争摧残的爱情悲剧。女主人公“戍妇”与丈夫从小青梅竹马,结为连理之后夫妻更是恩爱甚笃,然而好景不长,无情的战火打破了家庭幸福与宁静,丈夫被朝廷的“一纸诏书”征召从军,从此“一去无消息”,妻子对丈夫的思念之苦在十三年的守候中被不断放大。全诗通过对戍妇形象的塑造和戍妇对丈夫思念的描写,控诉了封建战争对平民百姓的摧残,讴歌了戍妇坚贞不渝的爱情。全诗共154句,770余字。)
妾对隆中坐,思君盼归颜。唧唧槐上雀,飞上五铢钱。
深秋十三载,经冬夏历年。年年望乡关,日暮孤棹边。
坞城埋青草,青冢塞上寒。自幼同连理,两小无猜疑。
青梅傍竹植,竹马两相依。① 山西共植树,山东采菊归。
郎言不效古,但此常年期。至今东篱下,人面对菊花。
菊花犹未改,陶潜归何处。② 十六入君门,妾自君家人。
朝耕南山陲,夜伴读书声。不求官侯达,不求门楣盈。
只愿长此往,携手不分离。自为君家妇,出入守门庭。
为晓三重制,度化四德遗。居家理机务,出家念家居。
尊贵亦尊贵,贫贱不能移。君夸妇贤德,虽苦亦有余。
只求家和气,上下无相欺。③ 草堂三秋叶,深阁四时春。
皇庭一纸书,征戍到梓门。门前凄凄草,门外犬吠声。
官吏苦无何,老母跪致词:“家中无男子,独此不幸人。
若为从戍去,一去无消息”④ 官吏苦无何,贱妾前致词。
妾至夫君前,临未无呜咽:“君妇自此别,相期更何年。
临别无甚言,数语君须记。一言征戍苦,朝晚自相顾。
无妾侍君身,衣食亦间疏。二言塞上寒,不似在家园。
行军车马后,烟火戍城前。三言男儿坚,勿以家为念。
男儿须自强,效古作前贤。自此别离后,天海各一边。
天海虽相距,亦有心相连。何年秋雁过,足雁系平安。⑤
君行复迟迟,妾怀惟君知。三步一回首,步步歩相思。⑥
行行复顿足,顿足复行行。疾趋至君前,凝噎已无音。⑦
执手看泪眼,一语谓夫君:“愿做湘神女,伴君塞上征”⑧
日暮鸣鸦晚,人归颐草深。自此一别后,音书无通往。
妾在岭南住,年年登高处。望穿湘江水,望断岭南路。
杂草蓬丛生,荒骨遗野路。君戍守边疆,夜夜尽望乡。
一声茄笛怨,痛断几人肠。夫君愁肠断,妾亦断愁肠。
此时南山下,处处遍菊花。花开人不在,花萎人自伤。
对话人憔悴,对人花凄凉。人花两相映,迷惘共彷徨。
一载盼君归,对镜容颜失。鸾凤已飞去,空留题镜诗。⑨
二载盼君归,旦暮念君痴。独坐楼台夜,黎衣俱已湿。
三载盼君归,妆临泪又垂。 湘妃竹下逸,断肠花上飞。⑩
四载盼君归,两鬓渐依稀。依稀鬓发里,依稀阑梦中。
五载盼君归,西山横翠微。本是妾妇泪,洗却山色嵬。
六载盼君归,燕雀也无声。冥冥枝上雀,黯黯隔年期。
七载盼君归,流水更无音。无情悲花落,多情度伤悲。
别来十三载,载载念君归。雁落添残影,水流著江清。
人归人散后,月下月痕深。与君歌戍妇,凭古可堪今。
一曲歌未尽,自看古今人。
注释:
①李白《长干行》:“郎骑竹马来,绕床弄青梅。”
②典出陶潜:“采菊东篱下,悠然见南山。”
③“无”通“勿”,不要、别的意思。
④南朝齐宝月《估客乐》诗之二:“莫作瓶落井,一去无消息。”
⑤苏武牧羊,十九载,后系书与雁足,汉人见之,乃迎返。见《汉书·李广苏建传》。
⑥前两个“步”字作名词,意“脚步”;第三个“步”字作动词,意“生,出”。
⑦柳永《雨霖铃》:“执手相看泪眼,竟无语凝噎。”
⑧宋玉《高唐赋》:楚襄王与宋玉游云梦之台,望高唐之观。其上有云气变化无穷。玉谓此气为朝云,并对王说,过去先王曾游高唐,怠而昼寝,梦见一妇人,自称是巫山之女,愿侍王枕席,王因幸之。巫山之女临去时说:“妾在巫山之阳,高丘之阻,旦为朝云,暮为行雨,朝朝暮暮,阳台之下。”
⑨传楚王得一明镜,纹有鸾凤,一日凤离镜飞升,绕梁三日而去。李商隐《鸾凤》:“旧镜鸾何处,衰桐凤不栖。”鸾镜:装饰有鸾鸟图案的铜镜。鸾鸟是古代传说的神鸟。据《异苑》载“鸾睹镜中影则悲。”后人在诗中多以鸾镜表示临镜而生悲。
⑩湘妃竹:即斑竹,亦称“泪竹”,竿部生黑色斑点。这种竹子生长在湖南九嶷山中。《阵物志》:“尧之二女,舜之二妃,曰‘湘夫人’,舜崩,二妃啼,以涕汨挥,竹尽斑。”
断肠花:花名,其上多红色血斑,相传昔有一妇人,怀人不见,恒洒泪于北墙之下,后洒处生草,其花甚媚,色如妇面,其叶正绿反红,名曰断肠花。李白《古风》之十八:“天津三月时,千门桃与李,朝为断肠花,暮逐东流水。”
3. 2003年:《吊屈原赋》
作者:不详,2003年陕西考生。
尚记两千年前,贾公过长沙,自慨命运之不济,悒郁思索,而做斯赋。竟有同命相似之感叹,其悲叹人才之不为用,而忠言不被纳之意,盖与君之所行谬矣。命吾于考场之上,端午佳节,重做斯赋,以吊先生之灵
呜呼,君虽为楚王之同姓,其血缘之亲.可谓近矣,君累世为官,与楚王之忠心,可谓昭然也,然竟为世人所不容,被君王黜免,终于郁郁而沉于汩罗矣。虽有昭昭若明星之德,有日月齐辉之才,一旦被疏,不复被用,虽心系楚国,胸怀天下,岂不枉然。
余叹其感情之无用焉,君临天下,当以理为重,奈何信奸谗之语,而疏远信臣忠义之士也,怀王不用汝击,终招患祸,身死国灭,为天下笑,吾惟惜其不以事理相推,而竟以感情之草草行事也。
故天下之成就大事者,莫不恪守理,而自制于情也,人情莫不好悦己者,而恶直言者也,故庄宗虽有天下而终自戮于伶人之手,其沉溺于私情使然也。夫奸谗当道,以美色诱之,丝竹乐之,财物乱之,使其远正直而近谗邪,虽已似日之昏昏,而不自知,至于祸已至矣,乃有悔色,岂不晚哉?
人情有远近.而缘有亲疏,而公理无远近,正道无偏邪,君于九天之上,可忆及昔日否,子兰之流,力劝怀王之秦求和,终使怀王之魂留他乡,子兰岂不为楚王之亲近哉,有骨肉之亲,却不能远谋,有远谋之臣,未有骨肉之亲,情理相较,于情于理,竞何如哉,怀王屈理从情,终至斯地,虽有天地为其悲惜,然流留笑柄子青史矣。
君沉汩罗,去今两干余载矣,夫两千余载之中,屈理而从情者,不可尽数,今日光华闪耀大地,然此事仍无有断绝之时,余作此文,毕汝可知,展汝之盛德,示汝之才华,以警戒世人,使其屈情从理,如此,则官不贪,如此,则民不奸,如此则百姓直田享用不尽矣。
怀王于冥冥之中,定当后悔不迭,特以为情乃理之末,而理为情之始也,理从情而家不立,则国不治,则天下难平,情从理,则行路之人,可为骨肉之亲,邂逅之人,可助成大事,岂不如此哉?
[点评]立意切题,分析政治与感情的关系精辟;全篇用文言文写就,且文笔流畅,标点准确,显示出雄厚的古汉语基础知识;熟悉中国历史,把古代人物与现代人物结合起来对比,提升了主题;将中国的传统节日端午节自然结合进文章,生动感人,乃历年来很好的文章。《史记》里,司马迁为屈原和贾谊合写一传,可见这两位历史人物相似之处颇多,此文作者即以“贾公”开头,贴切而自然;而“我”的作赋,则顺理成章。主体部分紧紧围绕“以感情亲疏作为用人的标准,必将造成历史悲剧”这一中心,纵论历史,深入剖析,很具说服力。娴熟的文言笔法,读来韵味十足。文中可见《屈原列传》《谏太宗十思疏》《伶官传序》等课文的影子,足见考生对语文课本是熟悉的,文言基础知识掌握牢固,运用灵活,相关历史知识掌握也很不错。从对“赋”这种文体的要求来说,且不说汉赋,就是唐宋的赋,句式和声韵都应该“合律”--即多用骈句并讲究平仄。而这首赋在形式上还不大像,因为作赋太难,考生在考场上能作到这个程度就难能可贵了。不过后来者的借鉴宜审慎一些。
17.(2010年高考全国2卷理数19)如图,直三棱柱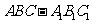 中,
中,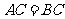 ,
,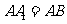 ,
,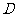 为
为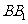 的中点,
的中点,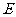 为
为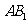 上的一点,
上的一点,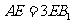 .
.
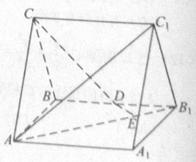 (Ⅰ)证明:
(Ⅰ)证明: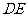 为异面直线
为异面直线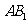 与
与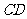 的公垂线;
的公垂线;
(Ⅱ)设异 面直线
面直线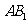 与
与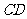 的夹角为45°,求二面角
的夹角为45°,求二面角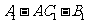 的大小.
的大小.
[命题意图]本试题主要考查空间的线面关系与空间角的求解,考查考生的空间想象与推理计算的能力.
16.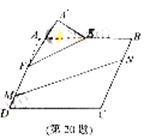 (2010年高考浙江卷理科20)(本题满分15分)如图,在矩形ABCD中,点E,F分别在线段AB,AD上,AE
=EB=AF=
(2010年高考浙江卷理科20)(本题满分15分)如图,在矩形ABCD中,点E,F分别在线段AB,AD上,AE
=EB=AF= 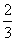 FD=4。沿直线EF将
FD=4。沿直线EF将 AEF翻着成
AEF翻着成 A‘EF,使平面A‘EF
A‘EF,使平面A‘EF 平面BEF。
平面BEF。
(Ⅰ)求二面角A‘-FD-C的余弦值;
(Ⅱ)点M,N分别在线段FD,BC上,若沿直线MN将四边形MNCD向上翻着,使C与A’重合,求线段FM的长。
(20)本题主要考察空间点、线、面位置关系,二面角等基础知识,空间向量的应用,同事考查空间想象能力和运算求解能力。满分15分。
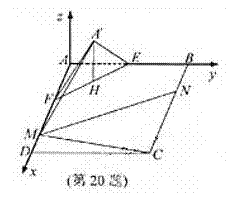 (Ⅰ)解:取线段EF的中点H,连结
(Ⅰ)解:取线段EF的中点H,连结 ,因为
,因为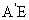 =
=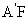 及H是EF的中点,所以
及H是EF的中点,所以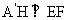 ,
,
又因为平面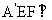 平面
平面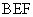 .
.
如图建立空间直角坐标系A-xyz
则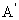 (2,2,
(2,2, ),C(10,8,0),
),C(10,8,0),
F(4,0,0),D(10,0,0).
故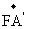 =(-2,2,2
=(-2,2,2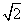 ),
),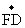 =(6,0,0).
=(6,0,0).
设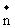 =(x,y,z)为平面
=(x,y,z)为平面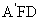 的一个法向量,
的一个法向量,
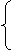 -2x+2y+2
-2x+2y+2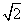 z=0
z=0
所以
6x=0.
取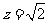 ,则
,则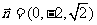 。
。
又平面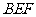 的一个法向量
的一个法向量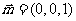 ,
,
故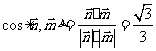 。
。
所以二面角的余弦值为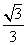
(Ⅱ)解:设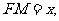 则
则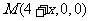 ,
,
因为翻折后,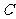 与
与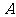 重合,所以
重合,所以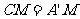 ,
,
故, 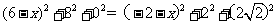 ,得
,得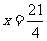 ,
,
经检验,此时点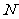 在线段
在线段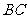 上,
上,
所以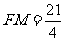 。
。
 方法二:
方法二:
(Ⅰ)解:取线段 的中点
的中点 ,
, 的中点
的中点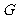 ,连结
,连结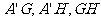 。
。
因为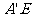 =
=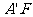 及
及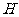 是
是 的中点,
的中点,
所以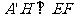
又因为平面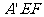
 平面
平面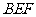 ,
,
所以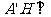 平面
平面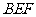 ,
,
又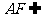 平面
平面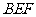 ,
,
故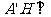
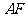 ,
,
又因为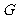 、
、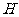 是
是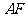 、
、 的中点,
的中点,
易知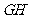 ∥
∥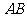 ,
,
所以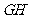

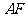 ,
,
于是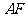
 面
面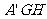 ,
,
所以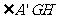 为二面角
为二面角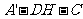 的平面角,
的平面角,
在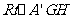 中,
中,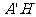 =
= ,
,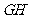 =2,
=2,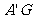 =
=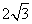
所以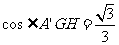 .
.
故二面角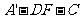 的余弦值为
的余弦值为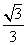 。
。
(Ⅱ)解:设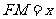 ,
,
因为翻折后,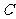 与
与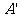 重合,
重合,
所以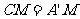 ,
,
而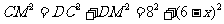 ,
,
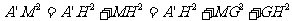
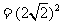
得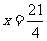 ,
,
经检验,此时点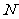 在线段
在线段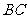 上,
上,
所以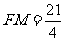 。
。
15.(2010年高考辽宁卷理科19)(本小题满分12分)
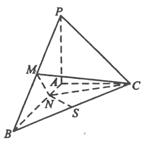 已知三棱锥P-ABC中,PA⊥ABC,AB⊥AC,PA=AC=½AB,N为AB上一点,AB=4AN,M,S分别
已知三棱锥P-ABC中,PA⊥ABC,AB⊥AC,PA=AC=½AB,N为AB上一点,AB=4AN,M,S分别 为PB,BC的中点.
为PB,BC的中点.
(Ⅰ)证明:CM⊥SN;
(Ⅱ)求SN与平面CMN所成角的大小.
20.(本小题满分12分)
解法一:(1)等体积法.
取CD中点O,连OB,OM,则OB=OM= ,OB⊥CD,MO⊥CD.
,OB⊥CD,MO⊥CD.
 又平面
又平面 平面
平面 ,则MO⊥平面
,则MO⊥平面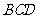 ,所以MO∥AB,MO∥平面ABC.M、O到平面ABC的距离相等.
,所以MO∥AB,MO∥平面ABC.M、O到平面ABC的距离相等.
作OH⊥BC于H,连MH,则MH⊥BC.
求得OH=OC•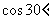 =
=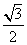 ,
,
MH=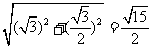 .
.
设点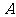 到平面
到平面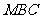 的距离为d,由
的距离为d,由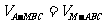 得
得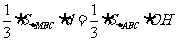 .
.
即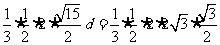 ,
,
解得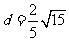 .
.
(2)延长AM、BO相交于E,连CE、DE,CE是平面 与平面
与平面 的交线.
的交线.
由(1)知,O是BE的中点,则BCED是菱形.
作BF⊥EC于F,连AF,则AF⊥EC,∠AFB就是二面角A-EC-B的平面角,设为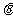 .
.
因为∠BCE=120°,所以∠BCF=60°.
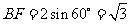 ,
,
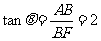 ,
,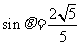 .
.
则所求二面角的正弦值为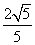
解法二:取CD中点O,连OB,OM,则
OB⊥CD,OM⊥CD.又平面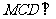 平面
平面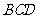 ,则MO⊥平面
,则MO⊥平面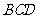 .
.
 取O为原点,直线OC、BO、OM为x轴、y轴、z轴,建立空间直角坐标系如图.OB=OM=
取O为原点,直线OC、BO、OM为x轴、y轴、z轴,建立空间直角坐标系如图.OB=OM= ,则各点坐标分别为C(1,0,0),M(0,0,
,则各点坐标分别为C(1,0,0),M(0,0, ),B(0,
),B(0,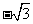 ,0),A(0,-
,0),A(0,- ,
,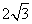 ).
).
(1)设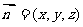 是平面MBC的法向量,则
是平面MBC的法向量,则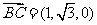 ,
,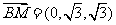 .
.
由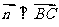 得
得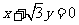 ;
;
由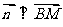 得
得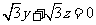 .
.
取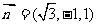 .
.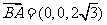 ,则
,则
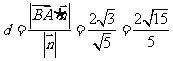 .
.
(2)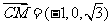 ,
,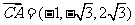 .
.

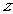 设平面ACM的法向量为
设平面ACM的法向量为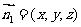 ,由
,由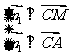 得
得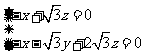 解得
解得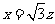 ,
,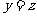 ,取
,取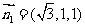 .又平面BCD的法向量为
.又平面BCD的法向量为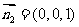 .
.
所以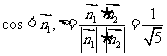 ,
,
设所求二面角为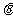 ,则
,则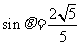 .
.
14.(2010年高考江西卷理科20)(本小题满分12分)
如图,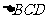 与
与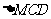 都是边长为2的正三角形,
都是边长为2的正三角形,
 平面
平面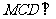 平面
平面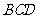 ,
,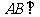 平面
平面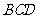 ,
,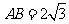 .
.
(1)求点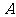 到平面
到平面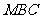 的距离;
的距离;
(2)求平面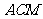 与平面
与平面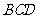 所成二面角的正弦值.
所成二面角的正弦值.
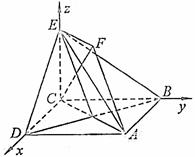
13.(2010年高考北京市理科16)(本小题共14分)
如图,正方形ABCD和四边形ACEF所在的平面互相垂直,CE⊥AC,EF∥AC,AB=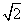 ,CE=EF=1.
,CE=EF=1.
 (Ⅰ)求证:AF∥平面BDE;
(Ⅰ)求证:AF∥平面BDE;
(Ⅱ)求证:CF⊥平面BDE;
(Ⅲ)求二面角A-BE-D的大小。
(16)(共14分)www.@ks@
证明:(I) 设AC与BD交与点G。
 因为EF//AG,且EF=1,AG=
因为EF//AG,且EF=1,AG=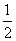 AC=1.
AC=1.
所以四边形AGEF为平行四边形.
所以AF//平面EG,
因为 平面BDE,AF
平面BDE,AF 平面BDE,
平面BDE,
所以AF//平面BDE.
(II)因为正方形ABCD和四边形ACEF所在的平面
相互垂直,且CE AC,
AC,
所以CE 平面ABCD.
平面ABCD.
如图,以C为原点,建立空间直角坐标系C-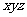 .
.
则C(0,0,0),A(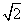 ,
,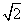 ,0),B(0,
,0),B(0,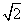 ,0).
,0).
所以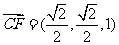 ,
,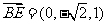 ,
,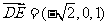 .
.
所以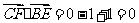 ,
,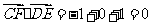
所以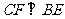 ,
,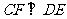 .
.
所以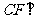 BDE.
BDE.
(III) 由(II)知,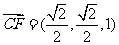 是平面BDE的一个法向量.
是平面BDE的一个法向量.
设平面ABE的法向量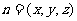 ,则
,则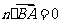 ,
,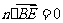 .
.
即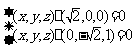
所以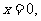 且
且
令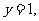 则
则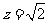 .
.
所以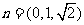 .
.
从而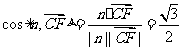 。
。
因为二面角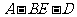 为锐角,
为锐角,
所以二面角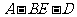 的大小为
的大小为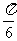 .
.
12.(2010年高考陕西卷理科18)(本小题满分12分)
如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA ⊥平面ABCD,AP=AB=2,BC=2 √ 2,E,F分别是AD,PC的重点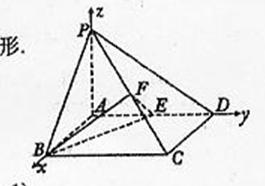
(Ⅰ)证明:PC ⊥平面BEF;
(Ⅱ)求平面BEF与平面BAP夹角的大小。
解法一 (Ⅰ)如图,以A为坐标原点,AB,AD,AP算在直线分别为x,y,z轴建立空间直角坐标系。
∵AP=AB=2,BC=AD=2√ 2,四边形ABCD是矩形。
∴A,B,C,D的坐标为A(0,0,0),B(2,0,0),C(2, 2 √ 2,0),D(0,2 √ 2,0),P(0,0,2)
又E,F分别是AD ,PC的中点,
,PC的中点,
∴E(0,√ 2,0),F(1,√ 2,1)。
∴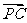 =(2,2 √ 2,-2)
=(2,2 √ 2,-2) =(-1,√ 2,1)
=(-1,√ 2,1) =(1,0,
=(1,0, 1),
1),
∴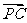 ·
· =-2+4-2=0,
=-2+4-2=0,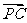 ·
· =2+0-2=0,
=2+0-2=0,
∴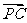 ⊥
⊥ ,
,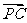 ⊥
⊥ ,
,
∴PC⊥BF,PC⊥EF,BF ∩ EF=F,
∴PC⊥平面BEF
(II)由(I)知平面BEF的法向量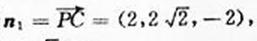
平面BAP 的法向量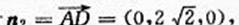
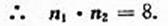 设平面BEF与平面BAP的夹角为 θ ,
设平面BEF与平面BAP的夹角为 θ ,
则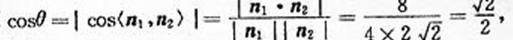
∴ θ=45℃, ∴ 平面BEF与平面BAP的夹角为45
解法二 (I)连接PE,EC在 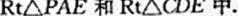
PA=AB=CD, AE=DE,
∴ PE= CE, 即 △PEC 是等腰三角形,
又F是PC 的中点,∴EF⊥PC,
又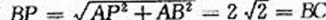 ,F是PC
的中点,
,F是PC
的中点,
∴BF⊥PC.
又

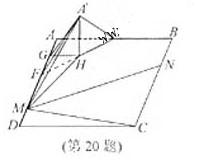
11. (2010年全国高考宁夏卷18)(本小题满分12分)
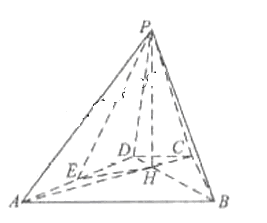 如图,已知四棱锥P-ABCD的底面为等腰梯形,AB
如图,已知四棱锥P-ABCD的底面为等腰梯形,AB CD,AC
CD,AC BD,垂足为H,PH是四棱锥的高 ,E为AD中点
BD,垂足为H,PH是四棱锥的高 ,E为AD中点
(1)
证明:PE BC
BC
(2)
若 APB=
APB= ADB=60°,求直线PA与平面PEH所成角的正弦值
ADB=60°,求直线PA与平面PEH所成角的正弦值
(18)解:
以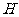 为原点,
为原点,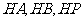 分别为
分别为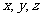 轴,线段
轴,线段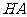 的长为单位长, 建立空间直角坐标系如图, 则
的长为单位长, 建立空间直角坐标系如图, 则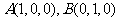
(Ⅰ)设 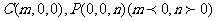
则 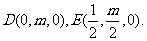
可得 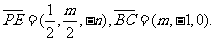
因为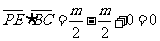
所以 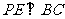

(Ⅱ)由已知条件可得
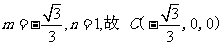

设 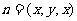 为平面
为平面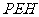 的法向量
的法向量
则 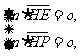 即
即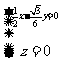
因此可以取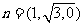 ,
,
由 ,
,
可得 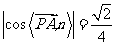
所以直线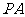 与平面
与平面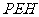 所成角的正弦值为
所成角的正弦值为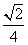
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com