
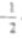 (13)已知a是第二象限的角tana=
(13)已知a是第二象限的角tana=
则cos a=___________.
的展开式中x3 的系数是__________
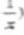 (14)x+
(14)x+
(15)已知抛物线C:y2
=2px(p>0)的准线为l,过M(1,0)且斜 率为√ 3的直线与l相交于A,与C的一个交点为B,若
率为√ 3的直线与l相交于A,与C的一个交点为B,若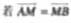 则p等于_________.
则p等于_________.
16 已知球O的半径为4,圆M与圆N为该球的两个小圈,AB为圆M与圆M的公共弦,AB=4,若OM=ON=3,则两圆圆心的距离MN=________________
(16)已知球O的半径为4,圆M与圆N为该球的两个小圆,AB为圆M与圆N的公共弦,AB=4,若两圆圆心距离MN=_____.
三 .解答题:本大题共6小题,共70分,解答应写出说明,证明过程或演算步骤。
.解答题:本大题共6小题,共70分,解答应写出说明,证明过程或演算步骤。
(17)(本小题满分10分)
三角形ABC中,D为边BC上的一点,BD=33,sinB= ,cos∠adc=
,cos∠adc= .求AD.
.求AD.
(18)(本小题满分12分)
已知{an}是各项均为正数的等比例数 列,且
列,且
A1+a2=2().a2+a3+a4=64( +
+ +
+ )
)
(Ⅰ)求{an}的通项公式;
(Ⅱ)设Bn=(an+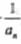 )2,求数列{bn}的前N项和Tn.[来源:Z§
)2,求数列{bn}的前N项和Tn.[来源:Z§
xx§]
(19)(本小题满分1 2分)
2分)
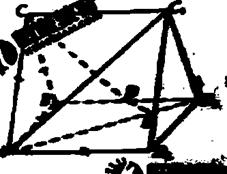
如图,直三棱柱ABC-A1B1C1中,AC=BC,AA1=AB,D为BB1的中点,E为AB1上的一点,AE=3EB1。
(Ⅰ)证明:DE为异面直线AB1与CD的公垂线;
(Ⅱ)DE为异面直线AB1与CD的夹角为45o,求二面角A1-AC1-B1的大小。
 [
[
(20)(本小题满分12分)
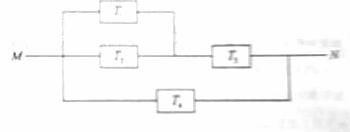
如图,由M到N的电路中有4个元件,分别标为T1,T2,T3,T4,电流能通过T1,T2,T3的概率都是P,电流能通过T4的概率是0.9.电流能否通过各元件相互独立。已知T1,T2,T3中至少有一个能通过电流的概率为0.999.
(Ⅰ)求P;
(Ⅱ)求电流能在M与N之间通过的概率。
(20)(本小题满分12分)
如图,由M到N的电路中有4各元件,分别为T1T2T3T 4。电流通过 T1T2T3的概率是 P ,电流能通过T 4的概率是0.9,电流量通过各元件相互独立,已知 T1T2T3中至少有一个能通过电源的概率为0.999
(1) 求P;
(2) 求电源能在M与N之间的概率
(21)(本小题满分12分)
已知函数f(x)=x3-3ax2+3x+1.
(1) 设 a=2 ,求f(x)的单调区间;
(2) 设f(x)在区间(2,3)中至少有一个极致点,求 a 的取值范围
(22)(本小题满分12分)
(21)(本小题满分12分)
已知函数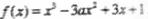
(Ⅰ)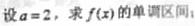
(Ⅱ)设 在区间(2、3)中至少有一个极值点,求a的取值范围
在区间(2、3)中至少有一个极值点,求a的取值范围
(22)(本小题满分12分)
已知斜率为1的直线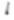 与双曲线
与双曲线 相交于B、D两点,且BD的中点为
相交于B、D两点,且BD的中点为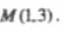

(Ⅰ)求C的离心率;
(Ⅱ)设C的右顶点为A,右焦点为F,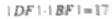 证明:过A、B、D
证明:过A、B、D 三点的圆与x轴相切。
三点的圆与x轴相切。
(1)设全 集U=
集U= ,集合A={1,3}。B={3,5},则
,集合A={1,3}。B={3,5},则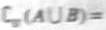 ( )
( )
(A){1,4} (b){1,5} (C){2,4} (D){2,4}
(2)不等式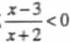 的解集为( )
的解集为( )
(A) (B)
(B)
(C)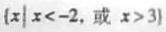
 (D){X∣X>3}
(D){X∣X>3}
(3)已知sina=2/3,则cos(π-2a)=
(A) 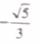 (B)
(B)
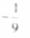 (C)
(C) 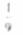 (D)
(D)
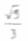
(4)函数y=1+ln(x-1)(x>1)的反函数是
(A) y=ex+1-1(x>0)
(B) y=ex+1+1(x >0)
>0)
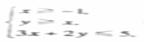 (C) y=ex+1-1 (x∈R)
(D) y=ex+1+1 (x∈R)
(C) y=ex+1-1 (x∈R)
(D) y=ex+1+1 (x∈R)
(5) 若变量x,y满足约束条件 ,则z=2x+y的最大值为
(A) 1 (B) 2 (C) 3 (D)4
(6)如果等差数列{an} 中,a4+a5+a6=12,那么 a1+a2+……+ an=
(A) 14 (B) 21 (C) 28 (D)35
(7) 若曲线y=x2+ax+b在点(0,b)处的切割线方程是x-y+1=0,则
(7)若曲线y= 在点(0.b)处的切线方程式
在点(0.b)处的切线方程式 =0,则
=0,则
(A)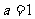 ,
,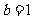 (B)
(B)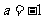 ,
,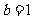
(C) 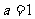 ,
,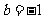 (D)
(D)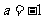
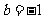
(8)已知三棱锥 中,底面ABC为变长等于2的等边三角形,SA垂直于底面ABC,SA=3,那么直线AB与平面SBC所成的角 的正弦值
中,底面ABC为变长等于2的等边三角形,SA垂直于底面ABC,SA=3,那么直线AB与平面SBC所成的角 的正弦值 为
为
(A) 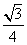 (B)
(B)  (C) (D)
(C) (D)
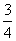
(9)将标号为1,2,3,4,5,6的6张卡放入3个不同的信封中,若每个信封放2张,其中标号为1,2的卡片放入同一信封,则不同的放法共有
(A) 12种 (B) 18种 (C) 36种 (D)54种
(10)△ABC种,点D在边AB上,CD平分∠ACB,若 =a,
=a,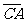 =b,|a| =1,|b|=2,则
=b,|a| =1,|b|=2,则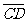 =[来
=[来
(A) 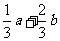 (B)
(B)  (C)
(C) 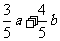 (D)
(D) 
(11)与正方体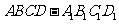 的三条棱
的三条棱 、
、 、AD所在直线距离相等的点
、AD所在直线距离相等的点
(A)有且只有1个
 (B)有且只有2个
(B)有且只有2个
2张,其中标号为1,2的卡片放入同一信封,则不同的放法共有
(A)12种  (B)18种 (C)16种 (D)54种
(B)18种 (C)16种 (D)54种
(10)△ABC中, 点D在边AB上,CD平分∠ABC B,若
点D在边AB上,CD平分∠ABC B,若 =a,
=a,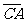 =b,∣a∣=1,
=b,∣a∣=1,
∣b∣=2,则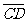 =
=
(A) a+
a+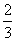 b
(B)
b
(B)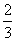 a+
a+ b (C)
b (C)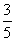 a+
a+ b (D)
b (D) a +
a +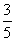 b
b
(11)与正方体ABCD-A1B1C1D1的三条棱AB、CC1
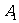 D所在直线的距离相等的点
D所在直线的距离相等的点
(A)有且只有1个 (B)有且只有2个 (C)有且只有3个 (D)有无数个
(12)已知椭圆C: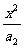 +
+ =1(a>b>0)的离心率为
=1(a>b>0)的离心率为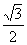 ,过右焦点F且斜率k(k>0)的直线与C相交于A、B亮点,若
,过右焦点F且斜率k(k>0)的直线与C相交于A、B亮点,若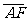 =3
=3 ,则k=
,则k=
(A)1
(B)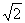 (C)
(C)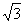 (D)2
(D)2
21.已知 是直角坐标平面
是直角坐标平面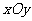 到自身的一个映射,点
到自身的一个映射,点 在映射
在映射 下的象为点
下的象为点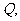 记作
记作
设 如果存在一个圆,使所有的点
如果存在一个圆,使所有的点
 都在这个圆内或圆上,那么称这个圆为点
都在这个圆内或圆上,那么称这个圆为点 的一个收敛圆. 特别地,当
的一个收敛圆. 特别地,当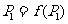 时,则称点
时,则称点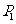 为映射
为映射 下的不动点.
下的不动点.
(1)若点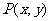 在映射
在映射 下的象为点
下的象为点
①求映射 下的不动点的坐标;
下的不动点的坐标;
②若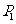 的坐标为
的坐标为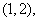 判断点
判断点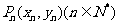 是否存在一个半径为3的收敛圆,并说明理由.
是否存在一个半径为3的收敛圆,并说明理由.
(2)若点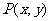 在映射
在映射 下的象为点
下的象为点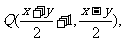 且
且
求证:点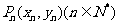 存在一个半径为
存在一个半径为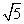 的收敛圆.
的收敛圆.
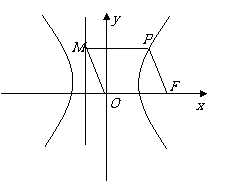
20.如图,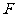 为双曲线
为双曲线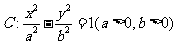 的右焦点,
的右焦点, 为双曲线
为双曲线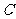 右支上一点,且位于
右支上一点,且位于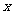 轴上方,
轴上方,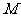 为左准线上一点,
为左准线上一点, 为坐标原点. 已知四边形
为坐标原点. 已知四边形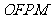 为菱形.
为菱形.
(1)求双曲线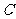 的离心率;
的离心率;
 (2)若经过焦点
(2)若经过焦点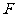 且平行于
且平行于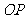 的直线交双曲线于
的直线交双曲线于 两点,且
两点,且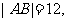 求此时的双曲线方程.
求此时的双曲线方程.
19.设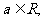 函数
函数
(1)当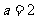 时,试确定函数
时,试确定函数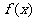 的单调区间;
的单调区间;
(2)若对于任何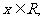 且
且 都有
都有 求
求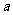 的取值范围.
的取值范围.
18. 如图,直三棱柱
如图,直三棱柱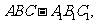
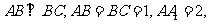
 是
是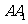 的中点.
的中点.
(1)求异面直线 与
与 所成角的大小;
所成角的大小;
(2)求二面角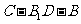 的大小;
的大小;
(3)在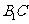 上是否存在一点
上是否存在一点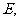 使得
使得 平面
平面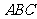 ?
?
若存在,求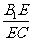 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
17.在一次抗洪抢险中,准备用射击的方法引爆从河上游漂流而下的一只巨大汽油罐.已知只有5发子弹备用,且首次命中只能使汽油流出,再次命中才能引爆成功.每次射击命中的概率都是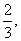 每次命中与否互相独立.
每次命中与否互相独立.
(理)(1)求恰好射击5次引爆油罐的概率;
(2)若引爆或子弹打光则停止射击,设射击次数为 求
求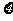 的分布列及数学期望.
的分布列及数学期望.
(文)(1)求恰好射击2次引爆油罐的概率;
(2)求恰好射击5次引爆油罐的概率.
16.在 中,角
中,角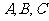 所对的边分别为
所对的边分别为 已知向量
已知向量 且
且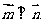
(1)求角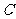 的大小; (2)若
的大小; (2)若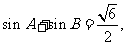 求角
求角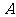 的值.
的值.
15.下图展示了一个由区间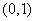 到实数集
到实数集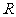 的映射过程:区间
的映射过程:区间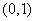 中的实数
中的实数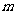 对应数轴上的点
对应数轴上的点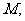 如图1;将线段
如图1;将线段 围成一个圆,使两端点
围成一个圆,使两端点 恰好重合,如图2;再将这个圆放在平面直角坐标系中,使其圆心在
恰好重合,如图2;再将这个圆放在平面直角坐标系中,使其圆心在 轴上,点
轴上,点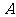 的坐标为
的坐标为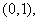 如图3,图3中直线
如图3,图3中直线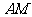 与
与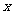 轴交于点
轴交于点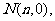 则
则
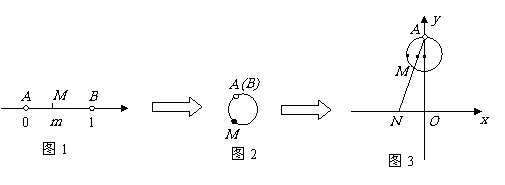
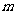 的象就是
的象就是 记作
记作
(1)方程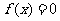 的解是
的解是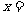 _______________;
_______________;
(2)下列说法中正确命题的序号是____________(填出所有正确命题的序号).
①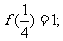 ②
②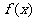 是奇函数;
是奇函数;
③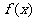 在定义域上单调递增; ④
在定义域上单调递增; ④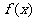 的图象关于点
的图象关于点 对称
对称
14.(理)已知集合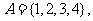 函数
函数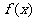 的定义域、值域都是
的定义域、值域都是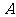 ,且对于任意
,且对于任意

设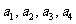 是1,2,3,4的任意一个排列,定义数表
是1,2,3,4的任意一个排列,定义数表 若两个数表的对应位置上至少有一个数不同,就说这是两张不同的数表,那么满足条件的不同的数表的张数为___________.
若两个数表的对应位置上至少有一个数不同,就说这是两张不同的数表,那么满足条件的不同的数表的张数为___________.
(文)6个人分乘两辆不同的出租车,若每辆车最多能乘4个人,则不同的乘车方案有_______种.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com