
2. 据报道,5月28日参观2010上海世博会的人数达35.6万﹒用科学记数法表示数35.6万
是( ▲ )
A.3.56×101 B.3.56×104 C.3.56×105 D.35.6×104
1. 在 -3,-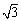 , -1, 0 这四个实数中,最大的是( ▲ )
, -1, 0 这四个实数中,最大的是( ▲ )
A. -3
B.-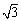 C. -1
D. 0
C. -1
D. 0
(17)(本小题满分12分)
已知函数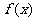 =2
=2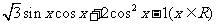 。
。
(1)求函数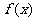 的最小正周期及在区间
的最小正周期及在区间 上的最大值和最小值:
上的最大值和最小值:
(2)若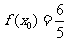 ,
,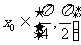 ,求
,求 的值。
的值。
[命题意图]本小题主要考查二倍角的正弦与余弦、两角和的正弦、函数 的性质、同角三角函数的基本关系、两角差的余弦等基础知识,考查基本运算能力。
的性质、同角三角函数的基本关系、两角差的余弦等基础知识,考查基本运算能力。
[解析](1)由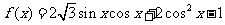 ,得
,得

所以函数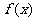 的最小正周期为
的最小正周期为
因为 在区间
在区间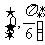 上为增函数,在区间
上为增函数,在区间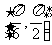 上为减函数,又
上为减函数,又
 ,所以函数
,所以函数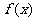 在区间
在区间 上的最大值为2,最小值为-1
上的最大值为2,最小值为-1
(2)解:由(1)可知
又因为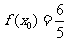 ,所以
,所以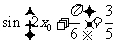
由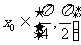 ,得
,得
从而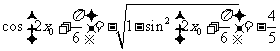
所以
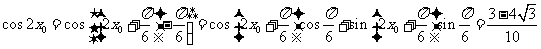 。
。
(18)(本小题满分12分)
某射手每次射击击中目标的概率是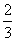 ,且各次射击的结果互不影响。
,且各次射击的结果互不影响。
(Ⅰ)假设这名射手射击5次,求恰有2次击中目标的概率:
(Ⅱ)假设这名射手射击5次,求有3次连续击中目标,另外2次未击中目标的概率:
(Ⅲ)假设这名射手射击3次,每次射击,击中目标得1分,未击中目标得0分,在3次射击中,若有2次连续击中,而另外1次未击中,则额外加1分;若3次全击中,则额外加3分,记ξ为射手射击3次后的总得分数,求ξ的分布列。
[命题意图]本小题主要考查二项分布及其概率计算公式、离散型随机变量的分布列、互斥事件和相互独立事件等基础知识,考查运用概率知识解决实际问题的能力。
[解析](1)解:设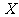 为射手在5次射击中击中目标的次数,则
为射手在5次射击中击中目标的次数,则 ~
~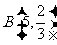 .在5次射击中,恰有2次击中目标的概率
.在5次射击中,恰有2次击中目标的概率

(Ⅱ)解:设“第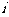 次射击击中目标”为事件
次射击击中目标”为事件 ;“射手在5次射击中,有3次连续击中目标,另外2次未击中目标”为事件
;“射手在5次射击中,有3次连续击中目标,另外2次未击中目标”为事件 ,则
,则

=

=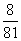
(Ⅲ)解:由题意可知,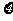 的所有可能取值为
的所有可能取值为
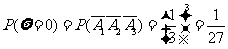
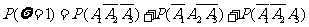
=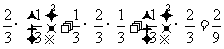
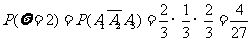

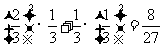
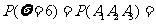
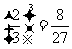
所以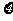 的分布列是
的分布列是
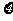 |
0 |
1 |
2 |
3 |
6 |
|
P |
 |
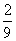 |
 |
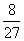 |
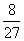 |
 (19)(本小题满分12分)
(19)(本小题满分12分)
如图,在长方体 中,
中,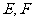 分别是棱
分别是棱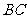 ,
,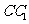 上的点,
上的点,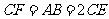 ,
,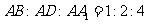 。
。
(Ⅰ)求异面直线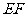 与
与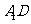 所成角的余弦值:
所成角的余弦值:
(Ⅱ)证明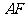 ⊥平面
⊥平面 :(Ⅲ) 求二面角
:(Ⅲ) 求二面角 的正弦值。
的正弦值。
[命题意图]本小题主要考查异面直线所成的角、直线与平面垂直、二面角等基础知识,考查用空间向量解决立体几何问题的方法,考查空间想象能力、运算能力和推理论证能力。
[解析]方法一:如图所示,建立空间直角坐标系,
点A为坐标原点,设 ,依题意得
,依题意得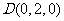 ,
,
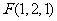 ,
,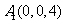 ,
,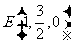
(1) 解:易得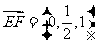 ,
,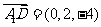
于是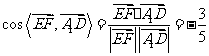
所以异面直线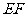 与
与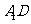 所成角的余弦值为
所成角的余弦值为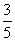
(2) 证明:已知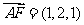 ,
,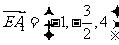 ,
,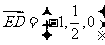
于是 ·
·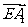 =0,
=0, ·
· =0.因此,
=0.因此,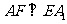 ,
,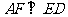 ,又
,又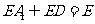
所以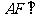 平面
平面
(3)解:设平面 的法向量
的法向量 ,则
,则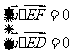 ,即
,即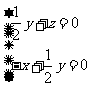
不妨令X=1,可得 。由(2)可知,
。由(2)可知,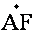 为平面
为平面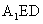 的一个法向量。
的一个法向量。
于是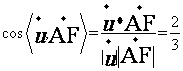 ,从而
,从而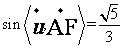
所以二面角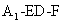 的正弦值为
的正弦值为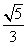
方法二:(1)解:设AB=1,可得AD=2,AA1=4,CF=1.CE=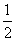
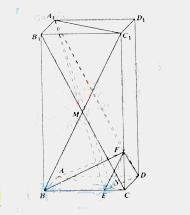 链接B1C,BC1,设B1C与BC1交于点M,易知A1D∥B1C,由
链接B1C,BC1,设B1C与BC1交于点M,易知A1D∥B1C,由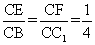 ,可知EF∥BC1.故
,可知EF∥BC1.故 是异面直线EF与A1D所成的角,易知BM=CM=
是异面直线EF与A1D所成的角,易知BM=CM=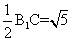 ,所以
,所以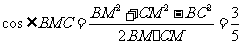 ,所以异面直线FE与A1D所成角的余弦值为
,所以异面直线FE与A1D所成角的余弦值为
(2)证明:连接AC,设AC与DE交点N 因为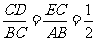 ,所以
,所以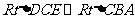 ,从而
,从而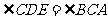 ,又由于
,又由于 ,所以
,所以 ,故AC⊥DE,又因为CC1⊥DE且
,故AC⊥DE,又因为CC1⊥DE且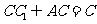 ,所以DE⊥平面ACF,从而AF⊥DE.
,所以DE⊥平面ACF,从而AF⊥DE.
连接BF,同理可证B1C⊥平面ABF,从而AF⊥B1C,所以AF⊥A1D因为 ,所以AF⊥平面A1ED
,所以AF⊥平面A1ED
(3)解:连接A1N.FN,由(2)可知DE⊥平面ACF,又NF 平面ACF, A1N
平面ACF, A1N 平面ACF,所以DE⊥NF,DE⊥A1N,故
平面ACF,所以DE⊥NF,DE⊥A1N,故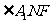 为二面角A1-ED-F的平面角
为二面角A1-ED-F的平面角
易知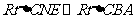 ,所以
,所以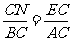 ,又
,又 所以
所以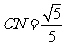 ,在
,在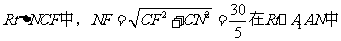
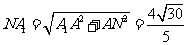
连接A1C1,A1F
在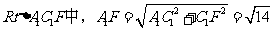
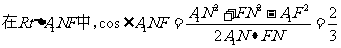 。所以
。所以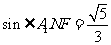
所以二面角A1-DE-F正弦值为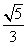 。
。
(20)(本小题满分12分)
已知椭圆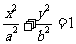 (
(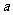 >
>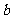 >0)的离心率
>0)的离心率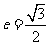 ,连接椭圆的四个顶点得到的菱形的面积为4。
,连接椭圆的四个顶点得到的菱形的面积为4。
(Ⅰ)求椭圆的方程:
(Ⅱ)设直线 与椭圆相交于不
与椭圆相交于不 同的两点
同的两点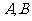 。已知点
。已知点 的坐标为(-
的坐标为(-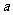 ,0),点
,0),点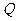 (0,
(0,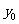 )在线段
)在线段 的垂直平分线上,且
的垂直平分线上,且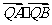 =4。求
=4。求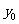 的值。
的值。
[命题意图]本小题主要考察椭圆的标准方程和几何性质,直线的方程,平面向量等基础知识,考查用代数方法研究圆锥曲线的性质及数形结合的思想,考查运算和推理能力。
[解析](1)解:由 ,得
,得 ,再由
,再由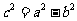 ,得
,得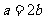
由题意可知, 
解方程组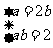 得 a=2,b=1
得 a=2,b=1
所以椭圆的方程为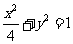
(2)解:由(1)可知A(-2,0)。设B点的坐标为(x1,,y1),直线l的斜率为k,则直线l的方程为y=k(x+2),
于是A,B两点的坐标满足方程组
由方程组消去Y并整理,得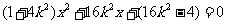
由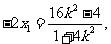 得
得
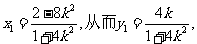
设线段AB是中点为M,则M的坐标为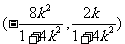
以下分两种情况:
(1)当k=0时,点B的坐标为(2,0)。线段AB的垂直平分线为y轴,于是
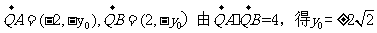
(2)当K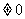 时,线段AB的垂直平分线方程为
时,线段AB的垂直平分线方程为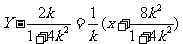
令x=0,解得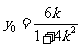
由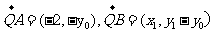
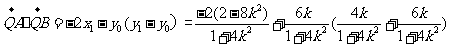
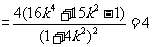
整理得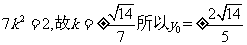
综上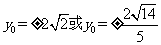 。
。
(21)(本小题满分14分)
已知函数f(x)=xe-x(x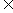 R).
R).
(Ⅰ) 求函数f(x)的单调区间和极值;
(Ⅱ)已知函数y=g(x)的图象与函数y=f(x)的图象关于直线x=1对称,证明当x>1时,f(x)>g(x)
(Ⅲ)如果 且
且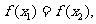 证明
证明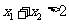
[命题意图]本小题主要考查导数的应用,利用导数研究函数的单调性与极值等基础知识,考查运算能力及用函数思想分析解决问题的能力。
[解析](Ⅰ)解:f’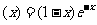
令f’(x)=0,解得x=1
当x变化时,f’(x),f(x)的变化情况如下表
|
X |
( ) ) |
1 |
( ) ) |
|
f’(x) |
+ |
0 |
- |
|
f(x) |
 |
极大值 |
 |
所以f(x)在( )内是增函数,在(
)内是增函数,在( )内是减函数。
)内是减函数。
函数f(x)在x=1处取得极大值f(1)且f(1)=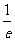
(Ⅱ)证明:由题意可知g(x)=f(2-x),得g(x)=(2-x)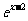
令F(x)=f(x)-g(x),即
于是
当x>1时,2x-2>0,从而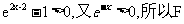 ’(x)>0,从而函数F(x)在[1,+∞)是增函数。
’(x)>0,从而函数F(x)在[1,+∞)是增函数。
又F(1)=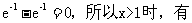 F(x)>F(1)=0,即f(x)>g(x).
F(x)>F(1)=0,即f(x)>g(x).
Ⅲ)证明:(1)
若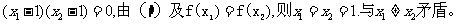
(2)若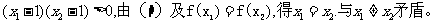
根据(1)(2)得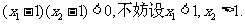
由(Ⅱ)可知,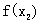 >
>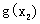 ,则
,则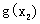 =
=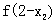 ,所以
,所以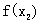 >
>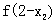 ,从而
,从而 >
>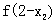 .因为
.因为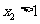 ,所以
,所以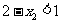 ,又由(Ⅰ)可知函数f(x)在区间(-∞,1)内事增函数,所以
,又由(Ⅰ)可知函数f(x)在区间(-∞,1)内事增函数,所以 >
>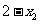 ,即
,即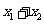 >2.
>2.
(22)(本小题满分14分)
在数列
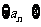 中,
中, ,且对任意
,且对任意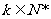
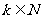 ,
,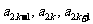 成等差数列,其公差为
成等差数列,其公差为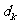 。
。
(Ⅰ)若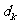 =2k,证明
=2k,证明 成等比数列(
成等比数列(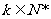 );
);
(Ⅱ)若对任意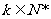 ,
, 成等比数列,其公比为
成等比数列,其公比为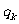 .
.
(i)设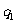
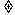 1.证明
1.证明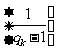 是等差数列;
是等差数列;
(ii)若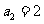 ,证明
,证明
[命题意图]本小题主要考查等差数列的定义及通项公式,前n项和公式、等比数列的定义、数列求和等基础知识,考查运算能力、推理论证能力、综合分析和解决问题的能力及分类讨论的思想方法。
[解析](Ⅰ)证明:由题设,可得 。
。
所以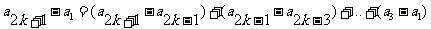
=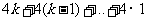
=2k(k+1)
由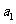 =0,得
=0,得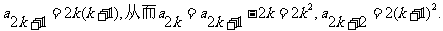
于是 。
。
所以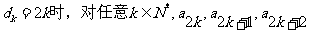 成等比数列。
成等比数列。
(Ⅱ)证法一:(i)证明:由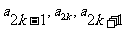 成等差数列,及
成等差数列,及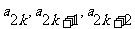 成等比数列,得
成等比数列,得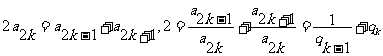
当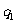 ≠1时,可知
≠1时,可知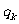 ≠1,k
≠1,k
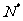
从而
所以 是等差数列,公差为1。
是等差数列,公差为1。
(Ⅱ)证明: ,
,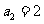 ,可得
,可得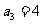 ,从而
,从而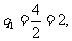
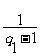 =1.由(Ⅰ)有
=1.由(Ⅰ)有
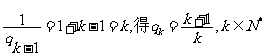
所以
因此,
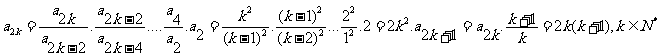 以下分两种情况进行讨论:
以下分两种情况进行讨论:
(1) 当n为偶数时,设n=2m(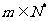 )
)
若m=1,则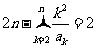 .
.
若m≥2,则
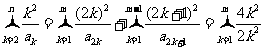 +
+
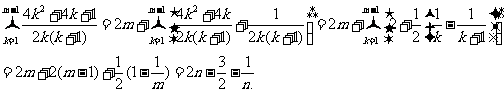
所以
(2)当n为奇数时,设n=2m+1(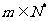 )
)
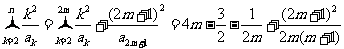
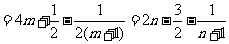
所以 从而
从而 ···
···
综合(1)(2)可知,对任意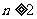 ,
,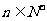 ,有
,有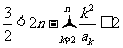
证法二:(i)证明:由题设,可得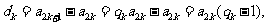
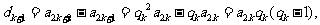 所以
所以

由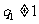 可知
可知 。可得
。可得 ,
,
所以 是等差数列,公差为1。
是等差数列,公差为1。
(ii)证明:因为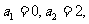 所以
所以 。
。
所以 ,从而
,从而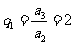 ,
,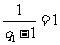 。于是,由(i)可知所以
。于是,由(i)可知所以 是公差为1的等差数列。由等差数列的通项公式可得
是公差为1的等差数列。由等差数列的通项公式可得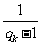 =
= 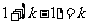 ,故
,故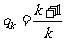 。
。
从而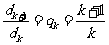 。
。
所以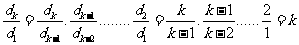 ,由
,由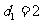 ,可得
,可得
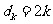 。
。
于是,由(i)可知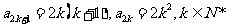
以下同证法一。
(11)甲、乙两人在10天中每天加工零件的个数用茎叶图表示下图,中间一列的数字表示零件个数,两边的数字表示零件个数的位数。则这10天甲、乙两人日加工零件的平均数分别为
和  。
。
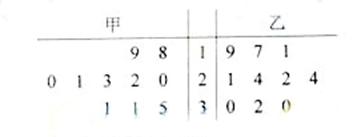
[答案]24,23
[解析]甲加工零件的平均数为
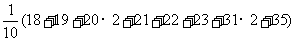 =24;
=24;
乙加工零件的平均数为
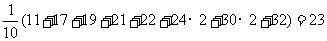 。
。
[命题意图]本题考查茎叶图的基础知识,属容易题。
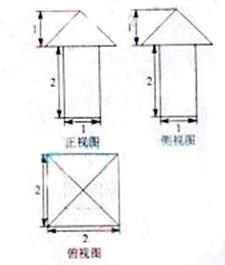
12. 一个几何体的三视图如图所示,则这个几何体的体积为 。
[答案]
[解析]由三视图知:该几何体是一个底面边长为1、高为2的正四棱柱与一个底面边长为2、高为1的正四棱锥组成的组合体.因为正四棱柱的体积为2, 正四棱锥的体积为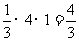 ,故该几何体的体积为
,故该几何体的体积为 .
.
[命题意图]本题考查立体几何中的三视图以及棱柱与棱锥体积的求解,考查空间想象能力、识图能力。
(13)已知圆C的圆心是直线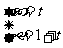 (
(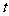 为参数)与
为参数)与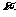 轴的交点,且圆C与直线
轴的交点,且圆C与直线 相切。则圆C的方程为
。
相切。则圆C的方程为
。
[答案]
[解析]令y=0得t=-1,所以直线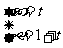 (
(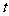 为参数)与
为参数)与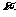 轴的交点为(-1,0),因为直线与圆相切,所以圆心到直线的距离等于半径,即
轴的交点为(-1,0),因为直线与圆相切,所以圆心到直线的距离等于半径,即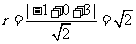 ,故圆C的方程为
,故圆C的方程为 。
。
[命题意图]本题考查直线的参数方程、圆的方程、直线与圆的位置关系等基础知识。
 (14)如图,四边形ABCD是圆O的内接四边形,延长A
(14)如图,四边形ABCD是圆O的内接四边形,延长A B和DC相交于点P。若
B和DC相交于点P。若 ,
,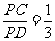 ,则
,则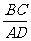 的值为
。
的值为
。
[答案]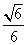
[解析]因为ABCD四点共圆,所以∠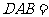 ∠PCB,
∠PCB,
∠CDA=∠PBC,因为∠P为公共角,所以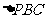 ∽
∽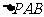 ,所以
,所以
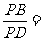
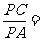
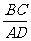 ,设PC=x,PB=y,则有
,设PC=x,PB=y,则有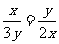 ,即
,即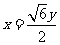 ,所以
,所以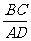 =
=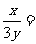
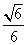 。
。
[命题意图]本题考查四点共圆与相似三角形的性质。
(15)如图,在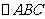 中,
中, ,
,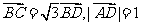 ,则
,则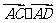 =
。
=
。

[答案]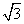
[解析]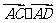 =
=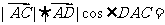
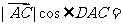
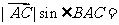
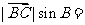
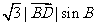 =
=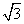 .
.
[命题意图]本题主要考查平面向量、解三角形等基础知识,考查化归与转化的数学思想,有点难度.
(16)设函数 ,对任
,对任 意
意 ,
,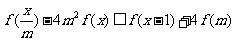
恒成立,则实数m的取值范围是 。
[[答案]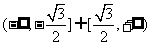
[解析]由题意知: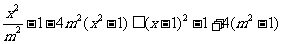 在
在 上恒成立,
上恒成立,
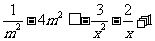 在
在 上恒成立,当
上恒成立,当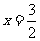 时,函数
时,函数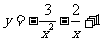 取得最小值
取得最小值 ,所以
,所以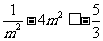 ,即
,即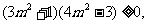 解得
解得 或
或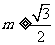 。
。
[命题意图]本题考查函数中的恒成立问题,考查化归与转化的数学思想。
90后出生的学生,思想特殊、行为方式和价值观令人担忧。假如你是一名90后出生的学生王林,请根据下表中所提供信息以“Do trust us-a generation born in the 90s”为题写一篇英语演讲稿,以消除人们的忧虑。
|
90后的境遇 |
面临更多的升学和就业烦恼,所处环境竞争更加激烈。 |
|
|
人们的忧虑 |
1.注重自我,轻视合作,…… 2.缺乏毅力,容易气馁,…… 3.盲目追求,渴望成名,…… |
|
|
我们的长处 |
敢于挑战,…… (请考生联系自己拟定内容,再列举两至三点。) |
|
注意:1.对所给要点,逐一陈述,适当发挥,不要简单翻译。
2.词数150左右。开头和结尾已经写好,不计入总词数。
3.演讲稿中不得提及考生所在班级及本人姓名。
4.参考词汇:盲目:blindly
Good afternoon, everyone!
The topic of my speech today is “Do trust us-a generation born in the 90s”.
Living in an environment full of fiercer competition, we, a generation born in the 90s, are faced with more problems in entering higher schools and getting employed. ____________________
____________________________________________________________________________________________________________________________________________________________
80. Five years after the International standards for digital TV were established ,_______(消费者)could have access to more than 200 channels in the USA.
79. The river water is used by the local people after being (净化).
78. After his ________(获得) of the diploma, he volunteered to work in the Northeast of China.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com