

21、已知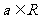 ,函数
,函数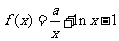 ,
, .
.
(1)求函数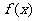 在区间
在区间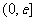 上的最小值;
上的最小值;
(2)是否存在实数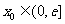 ,使曲线
,使曲线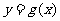 在点
在点 处的切线与
处的切线与 轴垂直?若存在,
轴垂直?若存在,
求出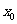 的值,若不存在,请说明理由;
的值,若不存在,请说明理由;
(3)求证: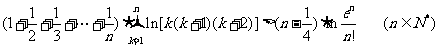 .
.
|
20、设椭圆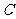 :
: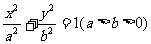 的左、右焦点分别为
的左、右焦点分别为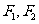 ,上顶点为
,上顶点为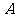 ,过点
,过点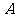 与
与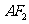 垂直的直线交
垂直的直线交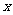 轴负半轴于点
轴负半轴于点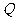 ,且
,且 .
.
(1)若过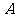 、
、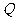 、
、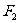 三点的圆恰好与直线
三点的圆恰好与直线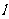 :
: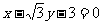 相切,求椭圆
相切,求椭圆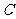 的方程;
的方程;
(2)在(1)的条件下,过右焦点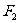 作斜率为
作斜率为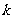 的直线
的直线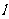 与椭圆
与椭圆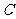 交于
交于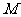 、
、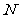 两点.
两点.
① 试证明: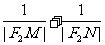 为定值;
为定值;
 ② 在
② 在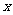 轴上是否存在点
轴上是否存在点 使得以
使得以 为邻边的平行四边形是菱形,如果存在,求出
为邻边的平行四边形是菱形,如果存在,求出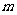 的取值范围,如果不存在,说明理由.
的取值范围,如果不存在,说明理由.
19、今年4月14日,冰岛南部艾雅法拉火山喷发,弥漫在欧洲上空多日的火山灰严重影响欧洲多个国家的多个机场的正常运营。据了解,受火山灰影响而取消的航班多达10万架次,给世界航空业带来的直接损失高达13亿美元,给人们的出行、社会的各项活动带来了很大的困难。因为风向的原因,该火山灰主要飘落在该火山口的东北方向与东南方向之间的欧洲大部,假设该火山喷发停止后,需要了解火山灰的飘散程度,为了测量的需要,若将距离该火山喷口中心50米内的扇形面记为第1区、50米至100米的扇环面记为第2区、....、第 米至
米至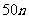 米的扇环面记为第n区、......,现测得第1区的火山灰平均每平方米为1吨、第2区每平方米的平均重量较第1区减少2%、第3区较第2 区又减少2%,若依次类推,问:
米的扇环面记为第n区、......,现测得第1区的火山灰平均每平方米为1吨、第2区每平方米的平均重量较第1区减少2%、第3区较第2 区又减少2%,若依次类推,问:
(1)离火山口1225米处的火山灰大约为每平方米多少千克?
(2)第几区内的火山灰总重量最大?
(3)该火山这次喷发的火山灰从第1区至第n 区的总重量为多少?(用含n的式子表示)
提示:当n较大时,可用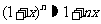 进行近似计算。
进行近似计算。
18、如图,正方形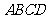 所在平面与
所在平面与 所在平面
所在平面 交于
交于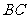 ,
,
且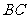 为
为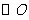 的弦,点
的弦,点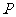 在
在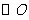 上,
上,
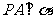 ,
,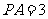 ,
,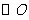 的直径为9.
的直径为9.
(1)求证: 为
为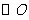 的直径;
的直径;
(2)试求正方形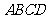 的边长
的边长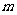 ;
;
(3)求平面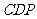 与平面
与平面 所成锐二面角
所成锐二面角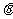 的余弦值.
的余弦值.
17、市二中高一某班级举行一次知识竞赛活动,活动分为初赛和决赛两个阶段、现将初赛答卷成绩(得分均为整数,满分为100分)进行统计,制成如下频率分布表.
|
分数(分数段) |
频数(人数) |
频率 |
|
[60,70) |
① |
0.16 |
|
[70,80) |
22 |
② |
|
[80,90) |
14 |
0.28 |
|
[90,100] |
③ |
④ |
|
合 计 |
50 |
1 |
(1)填充频率分布表中的空格(在解答中直接写出对应空格序号的答案);
(2)决赛规则如下:参加决赛的每位同学依次口答4道小题,答对2道题就终止答题,并获得一等奖。如果前三道题都答错,就不再答第四题。某同学进入决赛,每道题答对的概率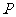 的值恰好与频率分布表中不少于80分的频率的值相同.
的值恰好与频率分布表中不少于80分的频率的值相同.
① 求该同学恰好答满4道题而获得一等奖的概率;
② 记该同学决赛中答题个数为 ,求
,求 的分布列及数学期望.
的分布列及数学期望.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com