
21.[选做题]在A,B,C,D四个小题中只能选做2个小题,每小题10分,共计20分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.
B.选修4-2 矩阵与变换
求矩阵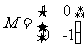 的特征值和特征向量,并计算
的特征值和特征向量,并计算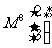 的值.
的值.
C.选修4-4:坐标系与参数方程
在平面直角坐标系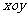 中,椭圆的参数方程为
中,椭圆的参数方程为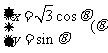 为参数).以
为参数).以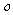 为极点,
为极点,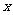 轴正半轴为极轴建立极坐标系,直线的极坐标方程为
轴正半轴为极轴建立极坐标系,直线的极坐标方程为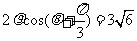 .求椭圆上点到直线距离的最大值和最小值.
.求椭圆上点到直线距离的最大值和最小值.
20. 已知函数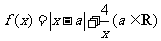 .
.
(1)若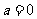 ,求不等式
,求不等式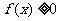 的解集;
的解集;
(2)当方程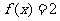 恰有两个实数根时,求
恰有两个实数根时,求 的值;
的值;
(3)若对于一切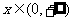 ,不等式
,不等式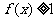 恒成立,求
恒成立,求 的取值范围.
的取值范围.
数 学 附 加 题
(考试时间30分钟,试卷满分40分)
19.已知数列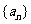 的前
的前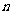 项和为
项和为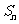 ,且满足
,且满足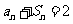 .
.
(1)求数列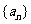 的通项公式;
的通项公式;
(2)求证数列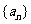 中不存在任意三项按原来顺序成等差数列;
中不存在任意三项按原来顺序成等差数列;
(3)若从数列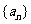 中依次抽取一个无限多项的等比数列,使它的所有项和
中依次抽取一个无限多项的等比数列,使它的所有项和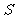 满足
满足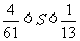 ,这样的等比数列有多少个?
,这样的等比数列有多少个?
18.某地区共有100户农民从事蔬菜种植,据调查,每户年均收入为3万元.为了调整产业
结构,当地政府决定动员部分种植户从事蔬菜加工.据估计,如果能动员x(x>0)户农民从
事蔬菜加工,那么剩下从事蔬菜种植的农民每户年均收入有望提高2x%,从事蔬菜加工的农
民每户年均收入为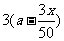 (
(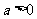 )万元。
)万元。
(1)在动员x户农民从事蔬菜加工后,要使从事蔬菜种植的农民的年总收入不低于动员前从事蔬菜种植的年总收入,试求x的取值范围;
(2)在(1)的条件下,要使这100户农民中从事蔬菜加工农民的年总收入始终不高于从事蔬菜种植农民的年总收入,试求实数 的最大值。
的最大值。
17.如图, 已知椭圆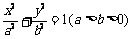 的长轴为
的长轴为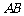 ,过点
,过点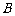 的直线
的直线 与
与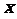 轴垂直.直线
轴垂直.直线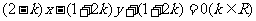 所经过的定点恰好是椭圆的一个顶点,且椭圆的离心率
所经过的定点恰好是椭圆的一个顶点,且椭圆的离心率 .
.
(1)求椭圆的标准方程;
 (2)设
(2)设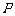 是椭圆上异于
是椭圆上异于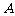 、
、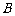 的任意一点,
的任意一点,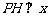 轴,
轴,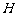 为垂足,延长
为垂足,延长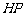 到点
到点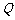 使得
使得 ,连结
,连结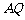 延长交直线
延长交直线 于点
于点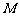 ,
,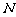 为
为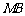 的中点.试判断直线
的中点.试判断直线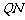 与以
与以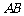 为直径的圆
为直径的圆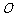 的位置关系.
的位置关系.
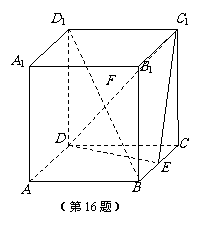
16.如图,在棱长为2的正方体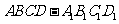 中,
中,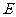 为
为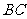 的中点,
的中点,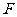 为
为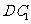 的中点.
的中点.
 (1)求证:
(1)求证: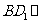 平面
平面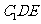 ;
;
(2)求三棱锥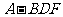 的体积.
的体积.
15.在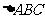 中,已知
中,已知 .
.
(1)求角B的度数;
(2)求 的取值范围.
的取值范围.
14.设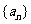 是一个公差为
是一个公差为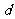 (
(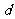 >0)的等差数列.若
>0)的等差数列.若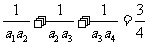 ,且其前6项的和
,且其前6项的和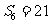 ,则
,则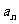 = ▲ .
= ▲ .
13.已知⊙A: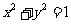 ,⊙B:
,⊙B: 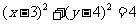 ,P是平面内一动点,过P作⊙A、⊙B的切线,切点分别为D、E,若
,P是平面内一动点,过P作⊙A、⊙B的切线,切点分别为D、E,若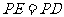 ,则P到坐标原点距离的最小值为 ▲ .
,则P到坐标原点距离的最小值为 ▲ .
12.若函数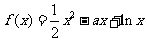 存在垂直于
存在垂直于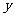 轴的切线,则实数
轴的切线,则实数 的取值范围是 ▲ .
的取值范围是 ▲ .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com