
19.(本小题满分14分)
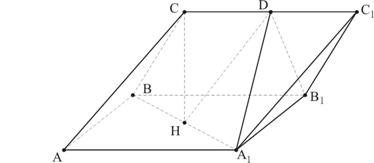
在三棱柱ABC-A1B1C1中,侧面AA1B1B是边长为2的正方形,点C在平面AA1B1B上的射影H恰好为A1B的中点,且CH=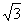 ,设D为
,设D为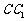 中点,
中点,
(1)求证: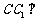 平面
平面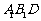 ;
;
 (2)求
(2)求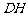 与平面
与平面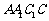 所成角的正弦值.
所成角的正弦值.
18.(本小题满分14分)
已知函数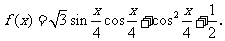
(1)求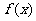 的周期和及其图象的对称中心;
的周期和及其图象的对称中心;
(2)在△ABC中,角A、B、C的对边分别是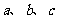 ,满足
,满足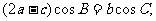 求函数
求函数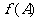 的取值范围.
的取值范围.
17.设函数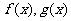 的定义域分别为
的定义域分别为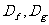 ,且
,且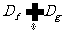 ,若
,若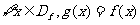 ,则函数
,则函数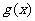 为
为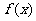 在
在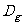 上的一个延拓函数.已知
上的一个延拓函数.已知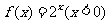 ,
,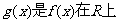 的一个延拓函数,且
的一个延拓函数,且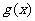 是奇函数,则
是奇函数,则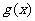 =________________
=________________
16.如果一条直线和一个平面垂直,则称此直线与平面构成一个“正交线面对”,在一个正方体中,由两个顶点确定的直线与含有四个顶点的平面构成“正交线面对”的概率为______.
15.若不等式组 表示的平面区域是一个三角形,则
表示的平面区域是一个三角形,则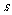 的取值范围是
.
的取值范围是
.
14.已知△AOB,点P在直线AB上,且满足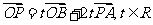 ,则
,则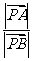 =_________
=_________
13.观察等式
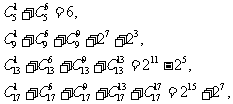
……
由以等式推测到一个一般的结论:
对于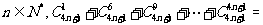 _______________.
_______________.
12.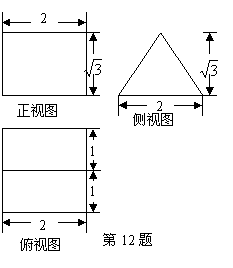 某几何体的三视图(单位:cm)如下图,则这个几何体的体积为_______cm3 .
某几何体的三视图(单位:cm)如下图,则这个几何体的体积为_______cm3 .
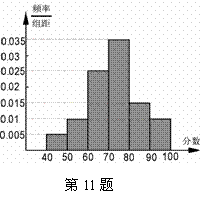
11.某大学对1000名学生的自主招生水平测试成绩进行统计,得到样本频率分布直方图如下图所示,现规定不低于70分为合格,则合格人数是
10.设定义域为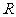 的函数
的函数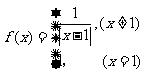
 ,若关于
,若关于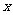 的方程
的方程 有且仅有三个不同的实数解
有且仅有三个不同的实数解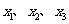 ,则
,则 ( )
( )
A.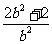 B.
B.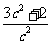 C.5 D.13
C.5 D.13
第II卷(共100分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com