
15.(全国卷2)一简谐横波以4m/s的波速沿x轴正方向传播。已知t=0时的波形如图所示,则

A.波的周期为1s
B.x=0处的质点在t=0时向y轴负向运动
C.x=0处的质点在t=  s时速度为0
s时速度为0
D.x=0处的质点在t=  s时速度值最大
s时速度值最大
答案:AB
解析:由波的图像可知半个波长是2m,波长是4m,周期是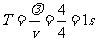 ,A正确。波在沿
,A正确。波在沿 轴正方向传播,则
轴正方向传播,则 =0的质点在沿
=0的质点在沿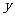 轴的负方向传播,B正确。x=0的质点的位移是振幅的一半则要运动到平衡位置的时间是
轴的负方向传播,B正确。x=0的质点的位移是振幅的一半则要运动到平衡位置的时间是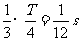 ,则
,则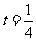 时刻x=0的质点越过了平衡位置速度不是最大,CD错误。
时刻x=0的质点越过了平衡位置速度不是最大,CD错误。
[命题意图与考点定位]本题属于波的图像的识图和对质点振动的判断。
6. (2010江苏卷)14、将边长为1m正三角形薄片,沿一条平行于底边的直线剪成两块,其中一块是梯形,记 ,则S的最小值是____▲____。
,则S的最小值是____▲____。
[解析] 考查函数中的建模应用,等价转化思想。一题多解。
设剪成的小 正三角形的边长为
正三角形的边长为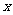 ,
, 则:
则: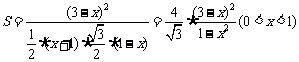
(方法一)利用导数求函数最小值。
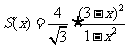 ,
,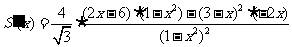

 ,
,
当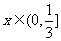 时,
时,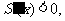 递减;当
递减;当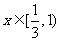 时,
时,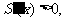 递增;
递增;
故当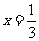 时,S的最小值是
时,S的最小值是 。
。
(方法二)利用函数的方法求最小值。
令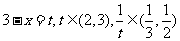 ,则:
,则:
故当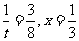 时,S的最小值是
时,S的最小值是 。
。
5. (2010江苏卷)11、已知函数 ,则满足不等式
,则满足不等式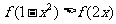 的x的
的x的 范围是__▲___。
范围是__▲___。
[解析] 考查分段函数的单调性。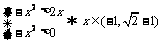
4. (2010江苏卷)5、设函数f(x)=x(ex+ ae-x)(x
ae-x)(x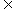 R)是偶函数,则实数
R)是偶函数,则实数 a=_______▲_________
a=_______▲_________
[解析]考查函数的奇偶性的知识。g(x)=ex+ae-x为奇函数,由g(0)=0,得a=-1。
3. (2010福建理数)15.已知定义域为 的函数
的函数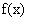 满足:①对任意
满足:①对任意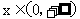 ,恒有
,恒有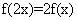 成立;当
成立;当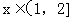 时,
时, 。给出如下结论:
。给出如下结论:
①对任意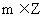 ,有
,有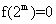 ;②函数
;②函数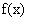 的值域为
的值域为 ;③存在
;③存在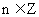 ,使
,使 得
得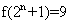 ;④“函数
;④“函数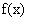 在区间
在区间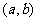 上单调递减”的充要条件是
“存在
上单调递减”的充要条件是
“存在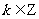 ,使得
,使得
 ”。
”。
其 中所有正确结论的序号是
。
中所有正确结论的序号是
。
[答案]①②④
[解析]对①,因为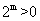 ,所以
,所以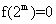 ,故①正确;经分析,容易得出②④也正确。
,故①正确;经分析,容易得出②④也正确。
[命题意图]本题考查函数的性质与充要条件,熟练基础知识是解答好本题的关键。
14.(2010湖南理数)过抛物线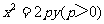 的焦点作斜率为1的
的焦点作斜率为1的 直线与该抛物线交于
直线与该抛物线交于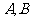 两点,
两点,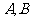 在
在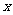 轴上的正射影分别为
轴上的正射影分别为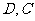 .若梯形
.若梯形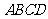
 的面积为
的面积为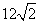 ,则
,则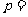 .
.

9. (1,+∞) .∵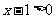 ,∴
,∴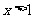 .
.
(2010广东文数)
(2010全国卷1理数)(15)直线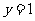 与曲线
与曲线 有四个交点,则
有四个交点,则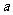 的取值范围是
.
的取值范围是
.

9.(2010广东理数) 函数 =lg(
=lg(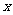 -2)的定义域是
.
-2)的定义域是
.
13.(2010陕西文数)已知函数f(x)=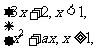 若f(f(0))=4a,则实数a= 2 .
若f(f(0))=4a,则实数a= 2 .
解析:f(0)=2,f(f(0))=f(2)=4+2a=4a,所以a=2
(2010重庆文数)(12)已知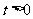 ,则函数
,则函数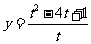 的最小值为____________ .
的最小值为____________ .
解析: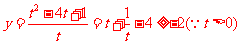 ,当且仅当
,当且仅当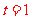 时,
时,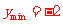
(2010浙江文数)(16) 某商家一月份至五月份累计销售额达3860万元,预测六月份销售额为500万元,七月份销售额比六月份递增x %,八月份销售额比七月份递增x%,九、十月份销售总额与七、八月份销售总额相等,若一月至十月份销售总额至少至少达7000万元,则,x 的最小值 。
%,八月份销售额比七月份递增x%,九、十月份销售总额与七、八月份销售总额相等,若一月至十月份销售总额至少至少达7000万元,则,x 的最小值 。
答案:20
(2010重庆理数)(15)已知函数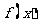 满足:
满足: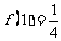 ,
,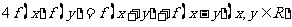 ,则
,则 =_____________.
=_____________.
解析:取x =1 y=0得
=1 y=0得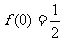
法一:通过计算 ,寻得周期为6
,寻得周期为6
法二:取x=n y=1,有f(n)=f(n+ 1)+f(n-1),同理f(n+1)=f(n+2)+f(n)
1)+f(n-1),同理f(n+1)=f(n+2)+f(n)
联立得f(n+2)= - f(n-1) 所以T=6 故
f(n-1) 所以T=6 故 =f(0)=
=f(0)= 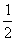
( 2010天津文数)(16)设函数f(x)=x-
2010天津文数)(16)设函数f(x)=x-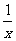 ,对任意x
,对任意x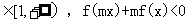 恒成立,则实数m的取值范围是________
恒成立,则实数m的取值范围是________
[答案]m<-1
[解析]本题主要考查了恒成立问题的基本解法及分类讨论思想,属于难题。
已知f(x)为增函数且m≠0
若m>0,由复合函数的单调性可知f(mx)和mf(x)均为增函数,此时不符合题意。
M<0,时有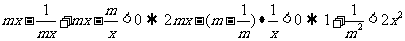 因为
因为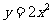 在
在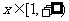 上的最小值为2,所以1+
上的最小值为2,所以1+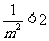 即
即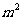 >1,解得m<-1.
>1,解得m<-1.
[温馨提示]本题是较为典型的恒成立问题,解决恒成立问题通常可以利用分离变量转化为最值 的方法求解。
的方法求解。
(2010天津理数)(16)设函数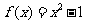 ,对任意
,对任意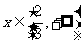 ,
,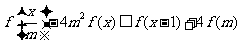 恒成立,则实数
恒成立,则实数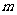 的取值范围是 .
的取值范围是 .
[答案]D
[解析]本题主要考查函数恒成立问题的基本解法,属于难题。
依据题意得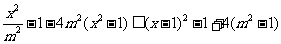 在
在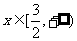 上恒定成立,即
上恒定成立,即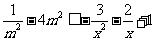 在
在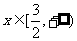 上恒成立。
上恒成立。
当 时函数
时函数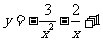 取得最小值
取得最小值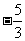 ,所以
,所以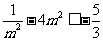 ,即
,即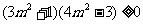 ,解得
,解得 或
或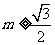
[温馨提示]本题是较为典型的恒成立问题,解决恒成立问题通常可以利用分离变量转化为最值的方法求解
10.(2010湖南文数)已知一种材料的最佳加入量在100g到200g之间,若用0.618法安排试验,则第一次试点的加入量可以是 g
[答案]171.8或148.2
[解析]根据0.618法,第一次试点加入量为
110+(210-110)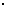 0.618=171.8
0.618=171.8
或 210-(210-110) 0.618=148.2
0.618=148.2
[命题意图]本题考察优选法的0.618法,属容易题。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com