
14.
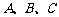 是球面上三点,且
是球面上三点,且 ,
,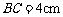 ,
, ,若球心
,若球心 到截面
到截面 的距离为
的距离为 ,则该球的表面积为
.
,则该球的表面积为
.
[解析](回归平几)如图,符合条件的△ABC是Rt三角形,∠BAC=90°.
设球心为O,取BO中点O1,连结OAO1, 则OO1⊥平面ABC,且
 cm,△OAO1中
cm,△OAO1中 .
.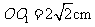 ,
,
故球半径 (cm),
(cm),
13.已知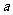 、
、 、
、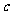 、
、 ,且满足下列两个条件:
,且满足下列两个条件:
①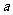 、
、 分别为回归直线方程
分别为回归直线方程 的常数项和一次项系数,其中
的常数项和一次项系数,其中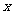 与
与 之间有如下对应数据:
之间有如下对应数据:
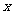 |
3 |
4 |
5 |
6 |
 |
2.5 |
3 |
4 |
4.5 |
② ;则
;则 的最小值是
.
的最小值是
.
[解析](转换,平均值不等式)显然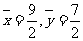 ,再根据线性回归公式计算出
,再根据线性回归公式计算出 .于是
.于是

12.已知函数 在
在 上连续,则
上连续,则 .
.
[解析](极限存在的条件)当x>0时, .当
.当 时,
时,
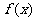 在R上连续,故必
在R上连续,故必 .于是
.于是
11.设函数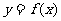 存在反函数
存在反函数 ,且函数
,且函数 的图象过点
的图象过点 ,则函数
,则函数 的图象一定过点 .
的图象一定过点 .
[解析](转换)已知函数 的图象过点
的图象过点 ,
, ,即
,即 .知函数
.知函数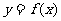 的图象过定点(2,1).其反函数
的图象过定点(2,1).其反函数 的图象过定点(1,2).
在
的图象过定点(1,2).
在 中,令x=1,得y=0.
中,令x=1,得y=0.
于是 的图象过定点(1,0).
的图象过定点(1,0).
10. 在四棱锥
在四棱锥 中,底面
中,底面 是边长为
是边长为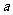 的正方形,顶点S
的正方形,顶点S
在底面内的射影O在正方形ABCD的内部(不在边上),且
, 为常数,设侧面
为常数,设侧面 与底面ABCD所成的二面角
与底面ABCD所成的二面角
依次为 ,则下列各式为常数的是
,则下列各式为常数的是
① ②
② ③
③ ④
④

A.①② B.②④ C.②③ D.③④
[解析](回归平几)如图过点O作正方形两邻边的平行线,分别交正方形各边
于E,F,G,H,连SE,SF,SG,SH.那么
 .
.
令OE=x,OG=y,OF=m,OH=n.则x+y=m+n=a.于是:
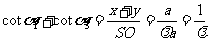 为常数.同理
为常数.同理
 为常数.故选B.
为常数.故选B.
9.若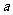 ,
, ,
, 且
且 ,则
,则 的最小值为同上
的最小值为同上
A. B.
B. C.
C. D.
D.
[解析](使用平均值不等式)由
已知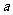 ,
, ,
, ,∴
,∴ .故选D.
.故选D.
8.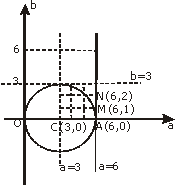 如果关于
如果关于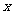 的一元二次方程
的一元二次方程 中,
中,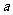 、
、 分别
分别
是两次投掷骰子所得的点数,则该二次方程有两个正根的概率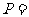
A. B.
B.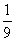 C.
C.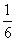 D.
D.
[解析1](图解法)显然 .基本事件总数为6×6=36.
.基本事件总数为6×6=36.
又方程 有二正根的条件是:
有二正根的条件是:

建立如图的直角坐标系,在可行域(1)内的正整数点只有M(6,1)和N(6,2)两个,故所求概率
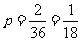 ,选A.
,选A.
[解析2](数据分析法)同上得出关系式(1)满足 的整数b只能为1,2.代入
的整数b只能为1,2.代入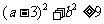 ,只能a=6,故适合(1)的正整数点只有M(6,1)和N(6,2)两个,故所求概率
,只能a=6,故适合(1)的正整数点只有M(6,1)和N(6,2)两个,故所求概率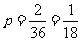 ,选A.
,选A.
7.将函数 的图象上所有点的横坐标伸长到原来的2倍,同时将纵坐标缩小到原来的
的图象上所有点的横坐标伸长到原来的2倍,同时将纵坐标缩小到原来的 倍,得到函数
倍,得到函数 的图象.另一方面函数
的图象.另一方面函数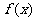 的图象也可以由函数
的图象也可以由函数 的图象按向量
的图象按向量 平移得到,则
平移得到,则 可以是 A.
可以是 A. B.
B. C.
C. D.
D.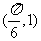
[解析1](逆向思维)将函数 的图象所有点的纵坐标扩大到原来的2倍,再将所有点的横坐标缩小为原来的
的图象所有点的纵坐标扩大到原来的2倍,再将所有点的横坐标缩小为原来的 ,得函数
,得函数 的图象.设点
的图象.设点 为函数
为函数 的图象上一点,有
的图象上一点,有 又设点
又设点 平移
平移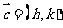 得(x,y)那么:
得(x,y)那么:

 代入(1):
代入(1):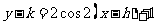 .
.
与 比较得:
比较得:
 ,故选A.
,故选A.
[解析2](取特殊点)如图,函数 图象的一个最高点为(0,3),函数
图象的一个最高点为(0,3),函数
图象的相应最高点为 .∵
.∵
 故选A.
故选A.
6.对于函数 的极值情况,3位同学有下列看法:
的极值情况,3位同学有下列看法:
甲:该函数必有2个极值;乙:该函数的极大值必大于1;丙:该函数的极小值必小于1;
这三种看法中,正确的的个数是 A.0个 B.1个 C.2个 D.3个
[解析](导数法) 时,
时, .令
.令 ,故
,故
方程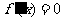 有相异二实根
有相异二实根 不妨设a>0,.易知:
不妨设a>0,.易知:
 ,函数
,函数 的单调情况如下表
的单调情况如下表
|
x |
 |
 |
 |
 |
 |
 |
+ |
0 |
- |
0 |
+ |
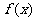 |
 |
极大值 |
 |
极小值 |
 |
由此可知:该函数必有2个极值,甲正确;
∵ ,且
,且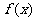 在
在 上为减函数,∴
上为减函数,∴ 乙正确;
乙正确;
 丙也正确.选D.
丙也正确.选D.
5. 是双曲线的两个焦点,Q是双曲线上任一点,从焦点
是双曲线的两个焦点,Q是双曲线上任一点,从焦点 引
引
 的平分线的垂线,垂足为P,则点P的轨迹为
的平分线的垂线,垂足为P,则点P的轨迹为
A.直线 B.圆 C.椭圆 D.双曲线
[解析](黑马一匹几何法)如图,延长 交于R,连OP.
交于R,连OP.
∵QP平分 ,且QP⊥F1R,,∴△Q F1R为等腰三角形,
,且QP⊥F1R,,∴△Q F1R为等腰三角形, 且P为F1R的中点.
且P为F1R的中点.
设双曲线实轴为2a,, ,而
,而
OP是△F1F2R的中位线, 为定值, 则点P的轨迹为圆,选B.
为定值, 则点P的轨迹为圆,选B.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com