
2. 右图表示吞噬细胞摄取和处理细菌、并呈
右图表示吞噬细胞摄取和处理细菌、并呈
递抗原的过程,图中MHC-Ⅱ分子是一种
特异性糖蛋白,能与抗原(图中的a)形成
抗原-MHC复合体,并移动到细胞的表面。
下列叙述正确的是( )
A.抗原a能被效应B细胞特异性识别
B.图中所示细胞器都属于生物膜系统
c.细胞②受刺激活化后将产生淋巴因子
D.细胞①只参与特异性免疫的感应阶段
1.下列四个生物实验中,操作顺序正确的是( )
A.观察植物细胞有丝分裂实验:取材→解离→染色→漂洗→制片→观察
B.蒲公英种群密度的取样调查:确定调查对象→选取样方→计数→计算种群密度
C.制作生态瓶实验:洗净空瓶→装入动植物→灌满自来水→密封瓶口→放在阳光下
D.温度对酶活性的影响实验:取试管→加入淀粉液→注入酶液→保温→加碘液→观察
21. 已知定义在实数集上的函数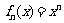 ,
,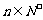 ,其导函数记为
,其导函数记为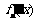 ,且满足:
,且满足:
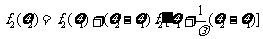
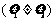 ,
,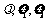 为常数.
为常数.
(Ⅰ)试求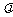 的值;
的值;
(Ⅱ)设函数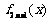 与
与 的乘积为函数
的乘积为函数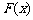 ,求
,求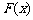 的极大值与极小值;
的极大值与极小值;
(Ⅲ)试讨论关于 的方程
的方程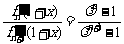 在区间
在区间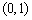 上的实数根的个数.
上的实数根的个数.
解:(Ⅰ)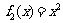 ,则
,则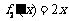 ,
,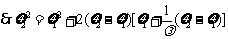 ,又
,又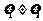 ,
,
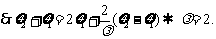
(Ⅱ)令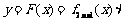
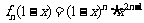 ,则
,则
 ,…3分
,…3分
令 ,得
,得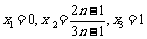 ,且
,且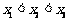 ,
,
当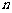 为正偶数时,随
为正偶数时,随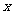 的变化,
的变化,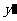 与
与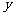 的变化如下:
的变化如下:
 |
 |
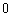 |
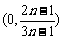 |
 |
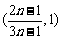 |
 |
 |
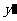 |
 |
0 |
 |
0 |
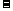 |
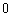 |
 |
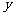 |
 |
|
 |
极大值 |
 |
极小值 |
 |
所以当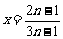 时,
时,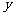 极大=
极大=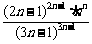 ;当
;当 时,
时,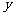 极小=0.
极小=0.
当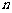 为正奇数时,随
为正奇数时,随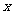 的变化,
的变化,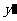 与
与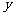 的变化如下:
的变化如下:
 |
 |
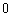 |
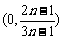 |
 |
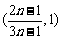 |
 |
 |
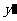 |
 |
0 |
 |
0 |
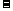 |
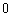 |
 |
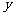 |
 |
|
 |
极大值 |
 |
|
 |
所以当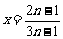 时,
时,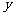 极大=
极大=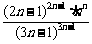 ;无极小值.
;无极小值.
(Ⅲ)由(Ⅰ)知,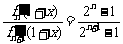 ,即
,即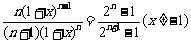 ,
,
所以方程为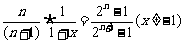 ,
,
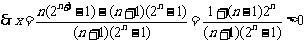 ,又
,又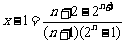 ,而对于
,而对于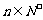 ,有
,有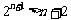 (利用二项式定理可证),
(利用二项式定理可证),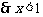 。
。
综上,对于任意给定的正整数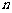 ,方程只有唯一实根,且总在区间
,方程只有唯一实根,且总在区间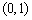 内,所以原方程在区间
内,所以原方程在区间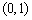 上有唯一实根.
上有唯一实根.
20.对于函数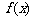 ,若存在
,若存在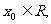 使得
使得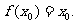 则称
则称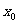 为函数
为函数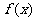 的一个不动点.比如函数
的一个不动点.比如函数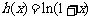 有唯一不动点
有唯一不动点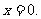 现已知函数
现已知函数 有且仅有两个不动点0和2.
有且仅有两个不动点0和2.
(Ⅰ)试求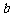 与
与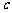 的关系式;
的关系式;
(Ⅱ)若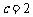 ,各项不为0的数列
,各项不为0的数列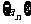 满足
满足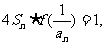 其中
其中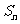 为
为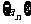 的前
的前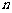 项和,试求
项和,试求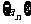 的通项公式;
的通项公式;
(Ⅲ)设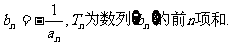 记
记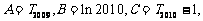 试比较A,B,C的大小,并说明理由.
试比较A,B,C的大小,并说明理由.
解:(Ⅰ)(理解不动点的含义)由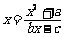 得,
得,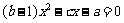 。由题设知
。由题设知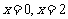 为该方程的两个根。
为该方程的两个根。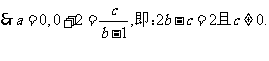
(Ⅱ)(寻找递推关系)若c=2,则b=2.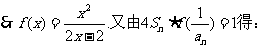
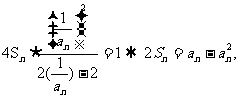 …①,又由
…①,又由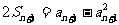 ………②
………②
②式-①式可得: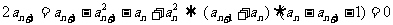

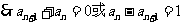
当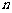 =1时,有
=1时,有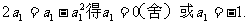
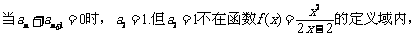
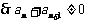
故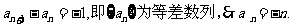
(Ⅲ)(构造)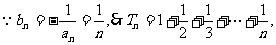
以下首先证明不等式
事实上要证
则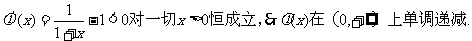
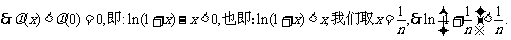
另一方面我们又设函数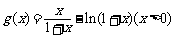 ,则
,则
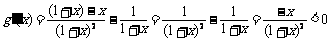 。
。
故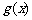 在
在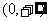 上单调递减,
上单调递减,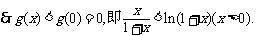
我们取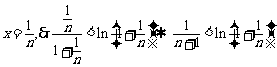
综上: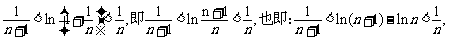
分别令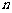 =1,2,3,…,2009得:
=1,2,3,…,2009得:

将这2009个式子累加得: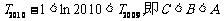
19. (Ⅰ) 解法一(定义法):设椭圆方程为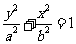
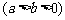 ,由已知
,由已知 。
。
又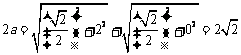 .所以
.所以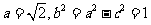 ,椭圆C的方程是
,椭圆C的方程是 +
+ 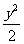 =1.
=1.
解法二(方程法):设椭圆方程为
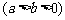 ,由已知
,由已知 ,即
,即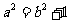 ,得
,得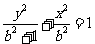
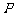 (
(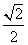 ,1)代入:
,1)代入: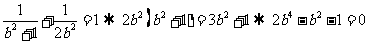
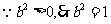
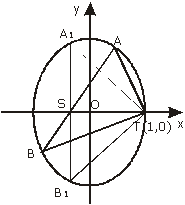 椭圆C的方程是
椭圆C的方程是 +
+ 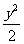 =1.
=1.
(Ⅱ)(先用特殊值探求,再证明探求的结果)在椭圆方程中,
令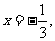 得
得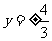 .如图即有:
.如图即有: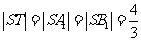 .这说明
.这说明
以弦A1B1为直径的圆过点T(1,0).以下我们证明:椭圆中过点
S的其他弦为直径的圆也过定点T(1,0)只需证明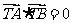 .
.
设直线AB: .代入椭圆方程,整理得:
.代入椭圆方程,整理得: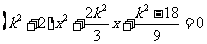 .
.
∵点S在椭圆内,∴此方程必有二实根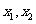 ,且
,且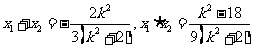 .于是
.于是
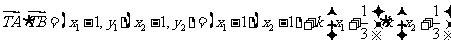
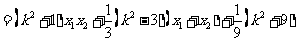
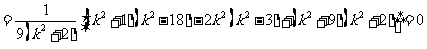
可知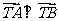 ,也就是任何其他弦为直径的圆都过定点T(1,0).
,也就是任何其他弦为直径的圆都过定点T(1,0).
以下两题用原解
19.以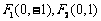 为焦点的椭圆
为焦点的椭圆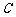 过点
过点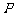 (
(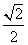 ,1).(Ⅰ)求椭圆
,1).(Ⅰ)求椭圆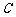 的方程;
的方程;
(Ⅱ)过点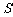 (
(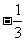 ,0)的动直线
,0)的动直线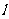 交椭圆
交椭圆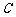 于
于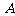 、
、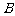 两点,试问:在坐标平面上是否存在一个定点
两点,试问:在坐标平面上是否存在一个定点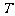 ,使得无论
,使得无论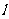 如何转动,以
如何转动,以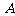
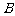 为直径的圆恒过点
为直径的圆恒过点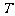 ? 若存在,求出点
? 若存在,求出点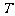 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
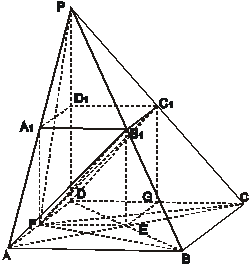
18. 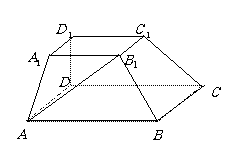 如图,在多面体
如图,在多面体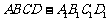 中,上、下两个底面
中,上、下两个底面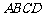 和
和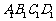 互相平行,且都是正方形,
互相平行,且都是正方形,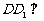 底面
底面 ,
,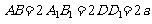 .
.
(Ⅰ)求异面直线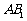 与
与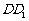 所成的角的余弦值;
所成的角的余弦值;
(Ⅱ)试在平面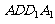 内确定一个点
内确定一个点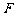 ,使得
,使得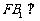 平面
平面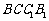 ;
;
(Ⅲ)在(Ⅱ)条件下,求二面角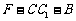 的余弦值.
的余弦值.
解:(补形与转换)如图,将原多面体“延长”成为四棱锥P-ABCD.则其中DA,DP,DC两两垂直..又作此棱锥的内接正方体A1B1C1D1-FEGD.设DA=DC=DP=2,则此正方体棱长为2.
(Ⅰ)∵DD1∥EB1, ∴∠AB1E是异面直线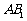 与
与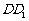 所成的角,设为α直角三角形AB1E中, B1E=1,
所成的角,设为α直角三角形AB1E中, B1E=1,
而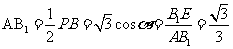 ,即
,即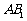 与
与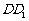 所成的角的余弦值为
所成的角的余弦值为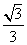
(Ⅱ)△PFB中FP=FB,且B1为PB的中点,
FB1⊥PB,又FB1⊥B1C1,∴FB1⊥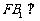 平面
平面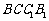
(Ⅲ)注意到△PFC,△PDC是以PC为公共底边
的等腰三角形,且C1为其中点,连DC1,FC1则
DC1⊥PC, FC1⊥PC,∠F C1D为二面角 的
的
平面角,设为θ,则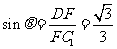
显然二面角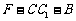 与
与 互余, 故其余弦值为
互余, 故其余弦值为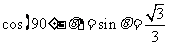
17.某种项目的射击比赛,开始时选手在距离目标100m处射击,若命中则记3分,且停止射击.若第一次射击未命中,可以进行第二次射击,但需在距离目标150m处,这时命中目标记2分,且停止射击.若第二次仍未命中,还可以进行第三次射击,此时需在距离目标200m处,若第三次命中则记1分,并停止射击.若三次都未命中则记0分,并停止射击.已知选手甲的命中率与目标的距离的平方成反比,他在100m处击中目标的概率为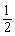 ,且各次射击都相互独立.(Ⅰ)求选手甲在三次射击中命中目标的概率;
,且各次射击都相互独立.(Ⅰ)求选手甲在三次射击中命中目标的概率;
(Ⅱ)设选手甲在比赛中的得分为 ,求
,求 的分布列和数学期望.
的分布列和数学期望.
解:记选手甲第一、二、三次射击命中目标分别为事件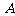 、
、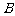 、
、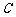 ,三次均为击中目标为事件
,三次均为击中目标为事件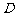 ,则
,则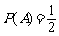 .
.
设选手甲在 m处击中目标的概率为
m处击中目标的概率为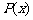 ,则
,则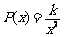 .由
.由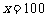 m时
m时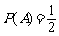 ,得
,得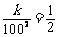 ,∴
,∴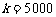 ,
,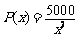 .∴
.∴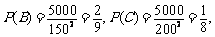
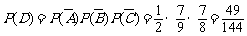 .
.
(Ⅰ)由于各次射击都是相互独立的,所以选手甲在三次射击中击中目标的概率为
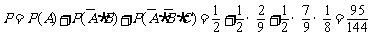 .
.
(Ⅱ)由题设知, 的可取值为
的可取值为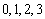 .
.
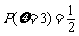 ,
,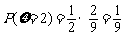 ,
,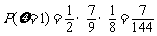 ,
, .
.
∴ 的分布列为
的分布列为
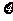 |
0 |
1 |
2 |
3 |
 |
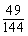 |
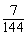 |
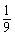 |
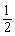 |
数学期望为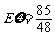 .
.
16.如图,已知O为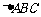 的外心,
的外心,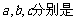 角A、B、C的对边,且满足
角A、B、C的对边,且满足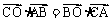 .
.
(Ⅰ)证明: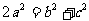 ; (Ⅱ)求
; (Ⅱ)求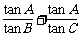 的值.
的值.
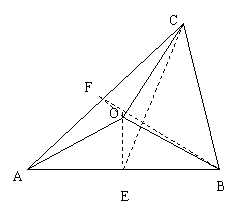 解:(Ⅰ)(向量,利用几何转换)取AB、AC的中点E、F,则
解:(Ⅰ)(向量,利用几何转换)取AB、AC的中点E、F,则
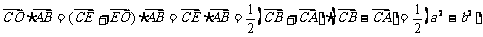
同理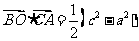 ;
;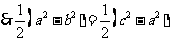
即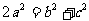 。
。
(Ⅱ)(解三角形)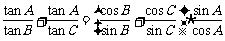
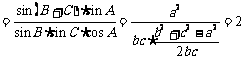
15.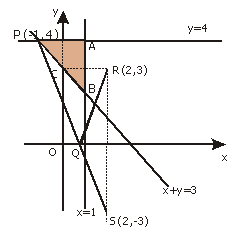 设
设 ,
,  是
是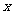 轴上一个动点,
轴上一个动点,
定点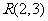 ,当点
,当点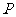 在
在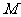 所表示的平面区域内运动时,设
所表示的平面区域内运动时,设
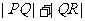 的最小值构成的集合为
的最小值构成的集合为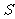 ,则
,则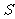 中最大的数是 .
中最大的数是 .
[解析](线性规划,回归平几)如图,点P的可行域为△ABP及其内部.
取P(0,4),作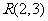 关于x轴的对称点
关于x轴的对称点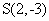 ,连SP交
,连SP交
x轴于Q,连RQ,那么所求S中最大的数即线段PS之长:
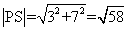 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com