
22.I am afraid we cannot include the item you suggest, as it does not __________ the rest of the programme.
A. come up with B. look down upon C. fit in with D. put up with
第一节:多项选择(共10小题;每小题1分,满分10分)
从A、B、C、D四个选项中,选出可以填入空白处的最佳选项,并在答题卡上将该项涂黑。
21.What I’ve said about him __________ anyone else who is never punctual for appointments. After all, nobody wants to be kept waiting.
A. makes for B. goes for C. stands for D. heads for
21.(本小题满分14分)
已知函数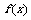 在其定义域上满足
在其定义域上满足 .
.
(1)函数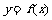 的图象是否是中心对称图形?若是,请指出其对称中心(不证明);
的图象是否是中心对称图形?若是,请指出其对称中心(不证明);
(2)当 时,求x的取值范围;
时,求x的取值范围;
(3)若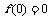 ,数列
,数列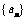 满足
满足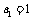 ,那么:
,那么:
①若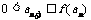 ,正整数N满足
,正整数N满足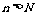 时,对所有适合上述条件的数列
时,对所有适合上述条件的数列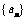 ,
, 恒成立,求最小的N;
恒成立,求最小的N;
②若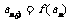 ,求证:
,求证: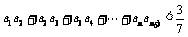 .
.
20.(本小题满分13分)
已知双曲线 的离心率为e,右顶点为A,左、右焦点分别为
的离心率为e,右顶点为A,左、右焦点分别为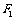 、
、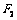 ,点E为右准线上的动点,
,点E为右准线上的动点,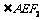 的最大值为
的最大值为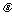 .
.
(1)若双曲线的左焦点为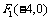 ,一条渐近线的方程为
,一条渐近线的方程为 ,求双曲线的方程;
,求双曲线的方程;
(2)求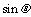 (用
(用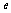 表示);
表示);
(3)如图,如果直线l与双曲线的交点为P、Q,与两条渐近线的交点为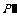 、
、 ,O为坐标原点,求证:
,O为坐标原点,求证: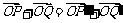 .
.

19.(本小题满分12分)
已知10件不同的产品中共有3件次品,现对它们进行一一测试,直到找出所有3件次品为止.
(1)求恰好在第5次测试时3件次品全部被测出的概率;
(2)记恰好在第k次测试时3件次品全部被测出的概率为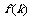 ,求
,求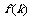 的最大值和最小值.
的最大值和最小值.
18.(本小题满分12分)
设函数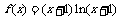 .
.
(1)求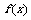 的单调区间;
的单调区间;
(2)若对所有的 ,均有
,均有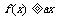 成立,求实数
成立,求实数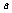 的取值范围.
的取值范围.
17.(本小题满分12分)
如图,在边长为a的正方体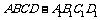 中,M、N、P、Q分别为AD、CD、
中,M、N、P、Q分别为AD、CD、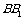 、
、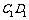 的中点.
的中点.
(1)求点P到平面MNQ的距离;
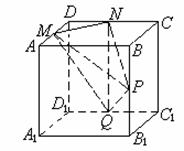
(2)求直线PN与平面MPQ所成角的正弦值.
16.(本小题满分12分)
在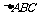 中,
中,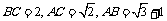 .
.
(1)求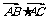 的值;
的值;
(2)若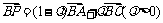 ,且
,且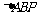 的面积为
的面积为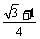 ,求实数
,求实数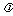 的值.
的值.
15.给出下列四个命题:
①“向量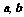 的夹角为锐角”的充要条件是“
的夹角为锐角”的充要条件是“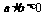 ”;
”;
②如果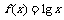 ,则对任意的
,则对任意的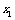 、
、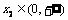 ,且
,且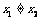 ,都有
,都有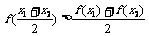 ;
;
③将4个不同的小球全部放入3个不同的盒子,使得每个盒子至少放入1个球,共有72种不同的放法;
④记函数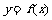 的反函数为
的反函数为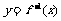 ,要得到
,要得到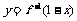 的图象,可以先将
的图象,可以先将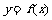 的图象关于直线
的图象关于直线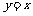 做对称变换,再将所得的图象关于y轴做对称变换,再将所得的图象沿x轴向左平移1个单位,即得到
做对称变换,再将所得的图象关于y轴做对称变换,再将所得的图象沿x轴向左平移1个单位,即得到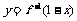 的图象.
的图象.
其中真命题的序号是 .(请写出所有真命题的序号)
14.计算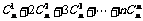 ,可以采用以下方法:
,可以采用以下方法:
构造恒等式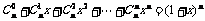 ,两边对x求导,得
,两边对x求导,得
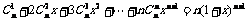 ,在上式中令
,在上式中令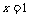 ,得
,得
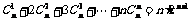 .
.
类比上述计算方法,计算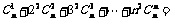 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com