
4.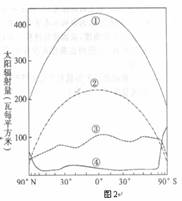 图中曲线中
( )
图中曲线中
( )
A.①表示云层反射的太阳辐射量
B.②表示大气上界的太阳辐射量
C.③表示地表吸收的太阳辐射量
D.④表示地表反射的太阳辐射量
3.由日本横滨开往旧金山的货轮,航行路线始终在300附近,其主要的原因是( )
A.顺西风漂流,节省燃料
B.航行距离短,节省时间
C.天气状况好,航行安全
D.过往船只少,不易拥堵
读到达地球太阳辐射量的分布图,图中曲线分别表示地表吸收太阳辐射量、地表反射太阳辐射量、大气上界太阳辐射量、云层反射太阳辐射量。回答4-6题。
2.2009年3月1日12时(区时),一艘由日本横滨
开往旧金山的货轮经过5分钟越过1800经线(如
图所示),此时其所在地点的区时是 ( )
A.3月2日12时5分
B.3月1日11时55分
C.2月28日12时5分
D.2月29日12时5分
1.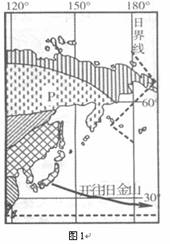 自然带P在大陆东岸分布纬度较低,其主要影
自然带P在大陆东岸分布纬度较低,其主要影
响因素是 ( )
A.地形因素
B.洋流因素
C.太阳辐射
D.大气环流
19.(12分)、随机抽查某地区高三年级100名学生的视力情况的频率分布直方图,如下图,已知前四组的频数成等比数列,后六组的频数成等差数列,组距为0.1,
(1)求视力在4.5和5.1之间的学生人数。
(2)求从这100名学生中任选一人其视力不低于5.0或不足4.5的概率。
(3)求从第 一组、第二组、第九组的学生中任抽2名,视力之和高于9.5的概率。
一组、第二组、第九组的学生中任抽2名,视力之和高于9.5的概率。

2 0.(13分)已知函数
0.(13分)已知函数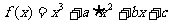 的图像上的一点
的图像上的一点 处的切线的方程为
处的切线的方程为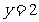 ,其中
,其中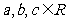
(Ⅰ)若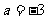 ①求
①求 的解析式。
的解析式。
②求证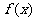 的图像关于点
的图像关于点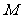 对称;
对称;
(Ⅱ)问函数y =f(x) 是否有单调减区间,若存在,求单调减区间(用 表示),若不
表示),若不
存在 ,请说明理由。
,请说明理由。
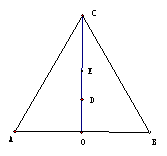
2 1.(14分)如图,在等边
1.(14分)如图,在等边 中,
中,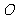 为边长
为边长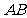 的中点,
的中点,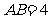 ,
,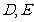 为
为 的高
的高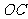 上的点,且
上的点,且 ,
,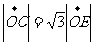 ;若以
;若以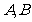 为焦点,
为焦点,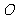 为中心的椭圆过
为中心的椭圆过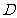 点,建立恰当的直角坐标系,记椭圆为
点,建立恰当的直角坐标系,记椭圆为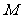
(Ⅰ)求椭圆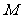 的轨迹方程;
的轨迹方程;
 (Ⅱ)过点
(Ⅱ)过点 的直线
的直线 与椭圆
与椭圆 交于不同的两点
交于不同的两点 ,点
,点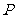 在点
在点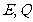 之间,且
之间,且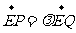 ,求实数
,求实数 的取值范围。
的取值范围。
18. (12分)如图,正方形ABCD所在平面与平面四边形ABEF所在平面互相垂直,△ABE是等腰
(12分)如图,正方形ABCD所在平面与平面四边形ABEF所在平面互相垂直,△ABE是等腰 直角三角形,AB=AE,FA=FE,∠AEF=45°.
直角三角形,AB=AE,FA=FE,∠AEF=45°.
(1)求 证:EF⊥平面BCE;
证:EF⊥平面BCE;
(2)设线段CD、AE的中点分别为P、M,求证:PM∥平面BCE;
17.(12分 )在
)在
 中,三个内角
中,三个内角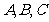 所对的边分别为
所对的边分别为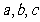
( ),
),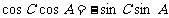 ,
,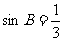
(1)求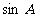 的值,
的值,
(2)若边长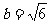 ,求
,求 的面积
的面积
16.(12分)设正数组成的数列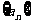 是等比数列,其前
是等比数列,其前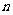 项和为
项和为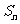 ,且
,且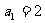 ,
, 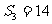
(1)求数列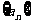 的通项公式;
的通项公式;
 (2)若
(2)若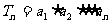 ,其中
,其中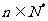 ; 求
; 求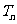 的值,并求
的值,并求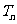 的最小值.
的最小值.
15.A(参数方程与 极坐标)
极坐标)
 直线
直线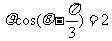 与直线
与直线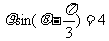 的交点直角坐标为
的交点直角坐标为
B.(不等式选讲)要使关于x的不等式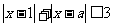 在实数
在实数
范围内有解,则a的取值范围是
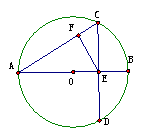
C. (几何证明 选讲)
如图所示,在圆O中,AB是圆O的直径
选讲)
如图所示,在圆O中,AB是圆O的直径
AB =8,E为OB的中点
 ,CD过点E且垂直于AB,EF⊥AC,则
,CD过点E且垂直于AB,EF⊥AC,则
CF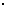 CA=
CA=
14.下列一组命题:
①在区间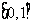 内任取两个实数
内任取两个实数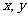 ,求事件“
,求事件“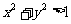 恒成立”的概率是
恒成立”的概率是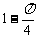
②从200个元素中抽取20个样本,若采用系统抽样的方法则应分为10组,每组抽取2个
③函数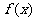 关
关 于(3,0)点对称,满足
于(3,0)点对称,满足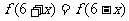 ,且当
,且当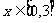 时函数为增函数,则
时函数为增函数,则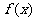 在
在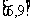 上为减函数。
上为减函数。
④命题“对任意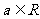 ,方程
,方程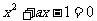 有实数解”的否定形式为“存在
有实数解”的否定形式为“存在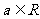 ,方程
,方程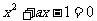 无实数解”
无实数解”
以上命题中正确的是
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com