
1.利用重锤下落验证机械能守恒定律的实验中,下面叙述正确的是( )
A.应该用天平称出物体的质量
B.应该选用点迹清晰,特别是第一点没有拉成长条的纸带
C.操作时应在接通电源的同时放开纸带
D.打点计时器应接在电压为4-6 V的直流电源上
答案:B
22.(安徽卷)(14分)质量为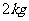 的物体在水平推力
的物体在水平推力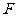 的作用下沿水平面作直线运动,一段时间后撤去
的作用下沿水平面作直线运动,一段时间后撤去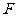 ,其运动的
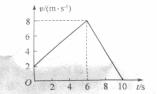
,其运动的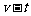 图像如图所示。
图像如图所示。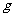 取
取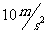 ,求:
,求:
(1)物体与水平面间的运动摩擦因数
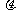 ;
;
(2)水平推力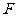 的大小;
的大小;
(3)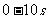 内物体运动位移的大小。
内物体运动位移的大小。
解析:
(1)设物体做匀减速直线运动的时间为△t2、初速度为v20、末速度为v2t、加速度为a2,则
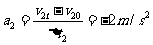 ①
①
设物体所受的摩擦力为Ff,根据牛顿第二定律,有
Ff=ma2 ②
Ff=-μmg ③
联立①②得
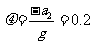 ④
④
(2)设物体做匀加速直线运动的时间为△t1、初速度为v10、末速度为v1t、加速度为a1,则
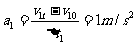 ⑤
⑤
根据牛顿第二定律,有
F+Ff=ma1 ⑥
联立③⑥得
F=μmg+ma1=6N
(3)解法一:由匀变速直线运动位移公式,得
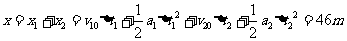
解法二:根据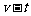 图象围成的面积,得
图象围成的面积,得
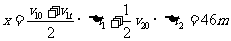
23.(四川卷)(16分)质量为M的拖拉机拉着耙来耙地,由静止开始做匀加速直线运动,在时间t内前进的距离为s。耙地时,拖拉机受到的牵引力恒为F,受到地面的阻力为自重的k倍,耙所受阻力恒定,连接杆质量不计且与水平面的夹角θ保持不变。求:

(1)拖拉机的加速度大小。
(2)拖拉机对连接杆的拉力大小。
(3)时间t内拖拉机对耙做的功。
[答案]⑴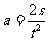
⑵
⑶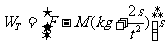
[解析]⑴拖拉机在时间t内匀加速前进s,根据位移公式
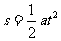 ①
①
变形得
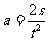 ②
②
⑵对拖拉机受到牵引力、支持力、重力、地面阻力和连杆拉力T,根据牛顿第二定律
 ③
③
②③连立变形得
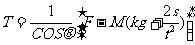 ④
④
根据牛顿第三定律连杆对耙的反作用力为
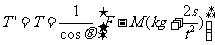 ⑤
⑤
(3)闭合开关调节滑动变阻器使待测表满偏,流过的电流为Im。根据并联电路电压相等有:
拖拉机对耙做功为
 ⑥
⑥
22.(福建卷)(20分)如图所示,物体A放在足够长的木板B上,木板B静止于水平面。t=0时,电动机通过水平细绳以恒力F拉木板B,使它做初速度为零,加速度aB=1.0m/s2的匀加速直线运动。已知A的质量mA和B的质量mg均为2.0kg,A、B之间的动摩擦因数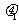 =0.05,B与水平面之间的动摩擦因数
=0.05,B与水平面之间的动摩擦因数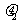 =0.1,最大静摩擦力与滑动摩擦力大小视为相等,重力加速度g取10m/s2。求
=0.1,最大静摩擦力与滑动摩擦力大小视为相等,重力加速度g取10m/s2。求
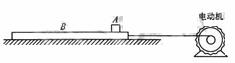
(1)物体A刚运动时的加速度aA
(2)t=1.0s时,电动机的输出功率P;
(3)若t=1.0s时,将电动机的输出功率立即调整为P`=5W,并在以后的运动过程中始终保持这一功率不变,t=3.8s时物体A的速度为1.2m/s。则在t=1.0s到t=3.8s这段时间内木板B的位移为多少?
解析:
(1)物体A在水平方向上受到向右的摩擦力,由牛顿第二定律得
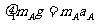
代入数据解得 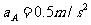
(2)t=1.0s,木板B的速度大小为
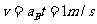
木板B所受拉力F,由牛顿第二定律有
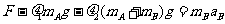
解得:F=7N
电动机输出功率
P= Fv=7W
(3)电动机的输出功率调整为5W时,设细绳对木板B的拉力为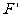 ,则
,则

解得 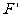 =5N
=5N
木板B受力满足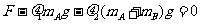
所以木板B将做匀速直线运动,而物体A则继续在B上做匀加速直线运动直到A、B速度相等。设这一过程时间为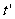 ,有
,有
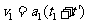
这段时间内的位移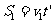 ④
④
A、B速度相同后,由于F> 且电动机输出功率恒定,A、B将一起做加速度逐渐减小的变加速运动,由动能定理有:
且电动机输出功率恒定,A、B将一起做加速度逐渐减小的变加速运动,由动能定理有:
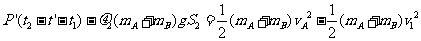
由以上各式代入数学解得:
木板B在t=1.0s到3.8s这段时间内的位移为: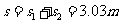
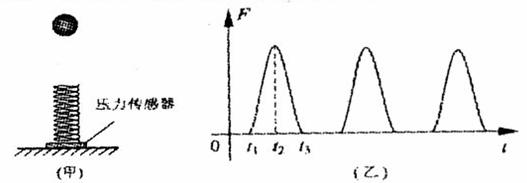
17、(福建卷)如图(甲)所示,质量不计的弹簧竖直固定在水平面上,t=0时刻,将一金属小球从弹簧正上方某一高度处由静止释放,小球落到弹簧上压缩弹簧到最低点,然后又被弹起离开弹簧,上升到一定高度后再下落,如此反复。通过安装在弹簧下端的压力传感器,测出这一过程弹簧弹力F随时间t变化的图像如图(乙)所示,则
A.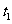 时刻小球动能最大
时刻小球动能最大
B. 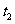 时刻小球动能最大
时刻小球动能最大
C. 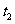 ~
~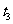 这段时间内,小球的动能先增加后减少
这段时间内,小球的动能先增加后减少
D. 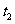 ~
~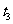 这段时间内,小球增加的动能等于弹簧减少的弹性势能
这段时间内,小球增加的动能等于弹簧减少的弹性势能
[答案]C
[解析]小球在接触弹簧之前做自由落体。碰到弹簧后先做加速度不断减小的加速运动,当加速度为0,即重力等于弹簧弹力时速度达到最大值,而后往下做加速度不断增大的减速K^S*5U运动,与弹簧接触的整个下降过程,小球的动能和重力势能转化为弹簧的弹性势能。上升过程恰好与下降过程互逆。由乙图可知t1时刻开始接触弹簧;t2时刻弹力最大,小球处在最低点,动能最小;t3时刻小球往上运动恰好要离开弹簧;t2-t3这段时间内,小球的先加速后减速,动能先增加后减小,弹簧的弹性势能转化为小球的动能和重力势能。
[命题特点]本题考查牛顿第二定律和传感器的应用,重点在于考查考生对图像的理解。
[启示]图像具有形象快捷的特点,考生应深入理解图像的含义并具备应用能力。
15.(江苏卷)(16分)制备纳米薄膜装置的工作电极可简化为真空中间距为d的两平行极板,如图甲所示,加在极板A、B间的电压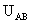 作周期性变化,其正向电压为
作周期性变化,其正向电压为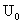 ,反向电压为
,反向电压为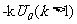 ,电压变化的周期为2r,如图乙所示。在t=0时,极板B附近的一个电子,质量为m、电荷量为e,受电场作用由静止开始运动。若整个运动过程中,电子未碰到极板A,且不考虑重力作用。
,电压变化的周期为2r,如图乙所示。在t=0时,极板B附近的一个电子,质量为m、电荷量为e,受电场作用由静止开始运动。若整个运动过程中,电子未碰到极板A,且不考虑重力作用。
(1)若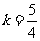 ,电子在0-2r时间内不能到达极板A,求d应满足的条件;
,电子在0-2r时间内不能到达极板A,求d应满足的条件;
(2)若电子在0-2r时间未碰到极板B,求此运动过程中电子速度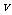 随时间t变化的关系;
随时间t变化的关系;
(3)若电子在第N个周期内的位移为零,求k的值。

解析:
(1)电子在0~T时间内做匀加速运动
加速度的大小 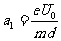 ①
①
位移 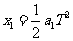 ②
②
在T-2T时间内先做匀减速运动,后反向作匀加速运动
加速度的大小 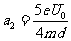 ③
③
初速度的大小 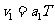 ④
④
匀减速运动阶段的位移 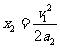 ⑤
⑤
依据题意 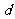 >
>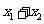 解得
解得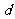 >
>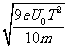 ⑥
⑥
(2)在2nT~(2n+1)T,(n=0,1,2, ……,99)时间内 ⑦
加速度的大小 a′2=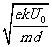
速度增量 △v2=-a′2T ⑧
(a)当0≤t-2nt<T时
电子的运动速度 v=n△v1+n△v2+a1(t-2nT) ⑨
解得 v=[t-(k+1)nT]
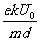 ,(n=0,1,2,
……,99) ⑩
,(n=0,1,2,
……,99) ⑩
(b)当0≤t-(2n+1)T<T时
电子的运动速度 v=(n+1) △v1+n△v2-a′2[t-(2n+1)T] 11
解得v=[(n+1)(k+1)T-kl]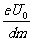 ,(n=0,1,2,
……,99) 12
,(n=0,1,2,
……,99) 12
(3)电子在2(N-1)T~(2N-1)T时间内的位移x2N-1=v2N-2T+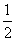 a1T2
a1T2
电子在(2N-1)T~2NT时间内的位移x2N=v2N-1T-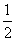 a′2T2
a′2T2
由10式可知 v2N-2=(N-1)(1-k)T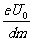
由12式可知 v2N-1=(N-Nk+k)T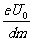
依据题意 x2N-1+ x2N=0
解得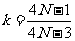
本题考查牛顿运动定律、运动学公式应用和归纳法解题。
难度:难。
32.(上海物理)(14分)如图,宽度L=0.5m的光滑金属框架MNPQ固定板个与水平面内,并处在磁感应强度大小B=0.4T,方向竖直向下的匀强磁场中,框架的电阻非均匀分布,将质量m=0.1kg,电阻可忽略的金属棒ab放置在框架上,并且框架接触良好,以P为坐标原点,PQ方向为x轴正方向建立坐标,金属棒从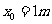 处以
处以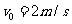 的初速度,沿x轴负方向做
的初速度,沿x轴负方向做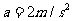 的匀减速直线运动,运动中金属棒仅受安培力作用。求:
的匀减速直线运动,运动中金属棒仅受安培力作用。求:
(1)金属棒ab运动0.5m,框架产生的焦耳热Q;
(2)框架中aNPb部分的电阻R随金属棒ab的位置x变化的函数关系;
(3)为求金属棒ab沿x轴负方向运动0.4s过程中通过ab的电量q,某同学解法为:先算出金属棒的运动距离s,以及0.4s时回路内的电阻R,然后代入
q=
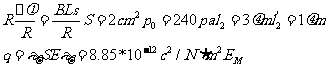 求解。指出该同学解法的错误之处,并用正确的方法解出结果。
求解。指出该同学解法的错误之处,并用正确的方法解出结果。
解析:
(1)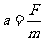 ,
,
因为运动中金属棒仅受安培力作用,所以F=BIL
又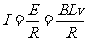 ,所以
,所以
且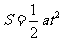 ,得
,得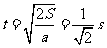
所以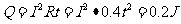
(2)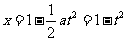 ,得
,得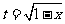 ,所以
,所以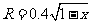 。
。
(3)错误之处:因框架的电阻非均匀分布,所求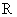 是0.4s时回路内的电阻R,不是平均值。
是0.4s时回路内的电阻R,不是平均值。
正确解法:因电流不变,所以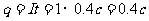 。
。
本题考查电磁感应、电路与牛顿定律、运动学公式的综合应用。难度:难。
11.(上海物理) 将一个物体以某一速度从地面竖直向上抛出,设物体在运动过程中所受空气阻力大小不变,则物体
(A)刚抛出时的速度最大 (B)在最高点的加速度为零
(C)上升时间大于下落时间 (D)上升时的加速度等于下落时的加速度
解析: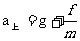 ,
,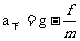 ,所以上升时的加速度大于下落时的加速度,D错误;
,所以上升时的加速度大于下落时的加速度,D错误;
根据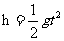 ,上升时间小于下落时间,C错误,B也错误,本题选A。
,上升时间小于下落时间,C错误,B也错误,本题选A。
本题考查牛顿运动定律和运动学公式。难度:中。
10.C.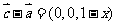 ,
,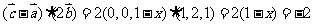 ,解得
,解得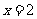 .
.
10.(2010广东理数)若向量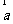 =(1,1,x),
=(1,1,x), 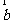 =(1,2,1),
=(1,2,1), 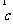 =(1,1,1),满足条件
=(1,1,1),满足条件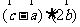 =-2,则
=-2,则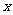 = .
= .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com