
21.(本小题满分14分)
已知函数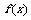 在其定义域上满足
在其定义域上满足 .
.
(1)函数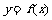 的图象是否是中心对称图形?若是,请指出其对称中心(不证明);
的图象是否是中心对称图形?若是,请指出其对称中心(不证明);
(2)当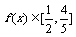 时,求x的取值范围;
时,求x的取值范围;
(3)若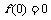 ,数列
,数列 满足
满足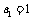 ,那么:
,那么:
①若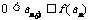 ,正整数N满足
,正整数N满足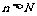 时,对所有适合上述条件的数列
时,对所有适合上述条件的数列 ,
,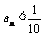 恒成立,求最小的N;
恒成立,求最小的N;
②若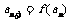 ,求证:
,求证: .
.
20.(本小题满分13分)
已知双曲线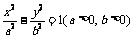 的离心率为e,右顶点为A,左、右焦点分别为
的离心率为e,右顶点为A,左、右焦点分别为 、
、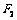 ,点E为右准线上的动点,
,点E为右准线上的动点, 的最大值为
的最大值为 .
.
(1)若双曲线的左焦点为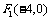 ,一条渐近线的方程为
,一条渐近线的方程为 ,求双曲线的方程;
,求双曲线的方程;
(2)求 (用
(用 表示);
表示);
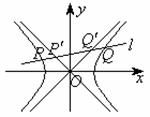
(3)如图,如果直线l与双曲线的交点为P、Q,与两条渐近线的交点为 、
、 ,O为坐标原点,求证:
,O为坐标原点,求证: .
.
19.(本小题满分12分)
已知10件不同的产品中共有3件次品,现对它们进行一一测试,直到找出所有3件次品为止.
(1)求恰好在第5次测试时3件次品全部被测出的概率;
(2)记恰好在第k次测试时3件次品全部被测出的概率为 ,求
,求 的最大值和最小值.
的最大值和最小值.
18.(本小题满分12分)
设函数 .
.
(1)求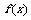 的单调区间;
的单调区间;
(2)若对所有的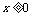 ,均有
,均有 成立,求实数
成立,求实数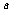 的取值范围.
的取值范围.
17.(本小题满分12分)
如图,在边长为a的正方体 中,M、N、P、Q分别为AD、CD、
中,M、N、P、Q分别为AD、CD、 、
、 的中点.
的中点.
(1)求点P到平面MNQ的距离;

(2)求直线PN与平面MPQ所成角的正弦值.
16.(本小题满分12分)
在 中,
中,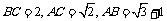 .
.
(1)求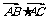 的值;
的值;
(2)若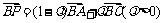 ,且
,且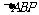 的面积为
的面积为 ,求实数
,求实数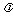 的值.
的值.
15.给出下列四个命题:
①“向量 的夹角为锐角”的充要条件是“
的夹角为锐角”的充要条件是“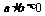 ”;
”;
②如果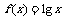 ,则对任意的
,则对任意的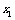 、
、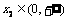 ,且
,且 ,都有
,都有 ;
;
③将4个不同的小球全部放入3个不同的盒子,使得每个盒子至少放入1个球,共有72种不同的放法;
④记函数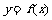 的反函数为
的反函数为 ,要得到
,要得到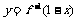 的图象,可以先将
的图象,可以先将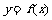 的图象关于直线
的图象关于直线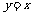 做对称变换,再将所得的图象关于y轴做对称变换,再将所得的图象沿x轴向左平移1个单位,即得到
做对称变换,再将所得的图象关于y轴做对称变换,再将所得的图象沿x轴向左平移1个单位,即得到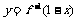 的图象.
的图象.
其中真命题的序号是 .(请写出所有真命题的序号)
14.计算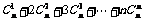 ,可以采用以下方法:
,可以采用以下方法:
构造恒等式 ,两边对x求导,得
,两边对x求导,得
 ,在上式中令
,在上式中令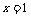 ,得
,得
 .
.
类比上述计算方法,计算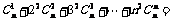 .
.
13.一次单元测验由50道选择题组成,每题选择正确得3分,不选或选错得0分,满分150分.若小明选对任一题的概率均为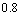 ,则小明在这次测验中成绩的标准差是 分.
,则小明在这次测验中成绩的标准差是 分.
12.若双曲线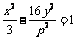 的左焦点在抛物线
的左焦点在抛物线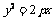 的准线上,则
的准线上,则 的值为 .
的值为 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com