
15.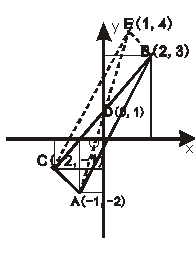 在平面直角坐标系xOy中,点A(-1,-2),B(2,3),C(-2,-1)
在平面直角坐标系xOy中,点A(-1,-2),B(2,3),C(-2,-1)
(1)求以线段AB、AC为邻边的平行四边形两条对角线的长
(2)设实数t满足(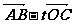 )·
)·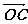 =0,求t的值
=0,求t的值
[分析]本题考查向量及其坐标运算,若借助平几知识,
则解法十分简单.是一道数形结合的好题,也是中等题.
[解析]⑴AB的中点为D(0,1),A(-1,-2)关于D(0,1)的对称点
为E(1,4).连EB,EC.则平行四边形ABEC的对角线之长分别为:
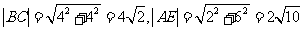
⑵已知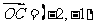 .由(
.由(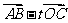 )·
)·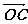 =0,得:
=0,得:

16如图,四棱锥P-ABCD中,PD⊥平面ABCD,PD=DC=BC=1,AB=2,AB∥DC,∠BCD=900
(1)求证:PC⊥BC
(2)求点A到平面PBC的距离
[分析]在立体几何试题中,本题怎么也称不上是难题.可是江苏考纲不要求考点面距离,所以这么简单的试题仍然属于“超纲”.一些老实备考的师生便吃了大亏.本题虽然简单却仍然“超纲”,命题人还是难辞其咎,这真是让人们哭笑不得的事.
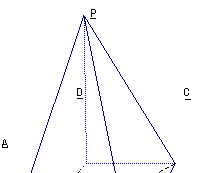 [解析](1)∵PD⊥平面ABCD,∴PD⊥BC;
[解析](1)∵PD⊥平面ABCD,∴PD⊥BC;
∵∠BCD=900∴BC⊥CD.故BC⊥平面PDC.从而
BC⊥PC.也就是PC⊥BC.
(2)连AC.设点A到平面PBC的距离为h.
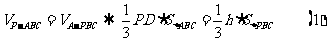
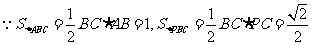 .
.
代入(1):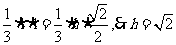 .即点A到平面PBC的距离为
.即点A到平面PBC的距离为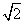 .
.
14.将边长为1的正三角形薄片,沿一条平行于底边的直线剪成两块,其中一块是梯形,记S= ,则S的最小值是_______▲_______
,则S的最小值是_______▲_______
[分析]本题构思简单精美,是小题中的难题,也是数形结合的好题可以用判别式法或导数法解出.
[解析1](判别式法)如图设BM=CM=x,则AM=AN=MN=1-x.作MH⊥BC于H,则
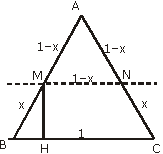
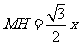 .梯形的周长为2+x,面积为
.梯形的周长为2+x,面积为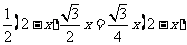
.于是:

即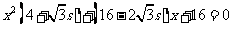 .此方程有实数解的条件是:
.此方程有实数解的条件是:
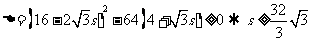 故所求s的最小值为
故所求s的最小值为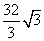
[解析2](导数法)同上得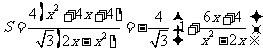
 .
.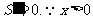 ,可知当
,可知当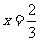 时
时
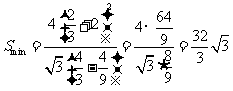
13.在锐角三角形ABC中,A、B、C的对边分别为a、b、c,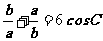 ,则
,则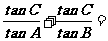 __ ▲
__ ▲
[分析]解本题需要借助正、余弦定理,正弦的和角公式以及弦与切的转换关系,一般学生难于找到正确的解题途径,是一道中等偏难的题,也是一道能力考查的好题
[解析]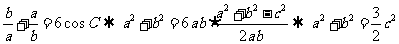
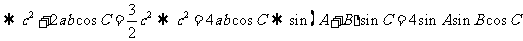
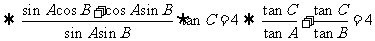
不过,作为无须写出解答过程的填空题,本题也可以通过取特值找到正确的答案.方法是:
取a=b=1,由条件得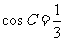 .以下通过解三角形,可以直接求出各角的正切值.
.以下通过解三角形,可以直接求出各角的正切值.
12.设实数x,y满足3≤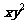 ≤8,4≤
≤8,4≤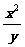 ≤9,则
≤9,则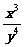 的最大值是_____▲____
的最大值是_____▲____
[分析]本题是中等题.若企图通过解不等式求解则会陷入困境.但若能想到配凑法则非常简单.所以也是一道好题
[解析] .故所求最大值为27.
.故所求最大值为27.
11.已知函数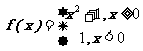 ,则满足不等式
,则满足不等式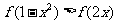 的x的范围是____▲____
的x的范围是____▲____
[分析]本题考查分段函数与不等式,需要详细的分类讨论,是一道中等偏难的题
[解析]严格地说,本题需分分4种情况讨论,然后取并集:
(1)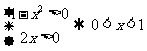 .此时
.此时
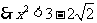 或
或 (与0<x<1不符,舍去).
(与0<x<1不符,舍去).
由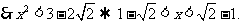 综合0<x<1,得
综合0<x<1,得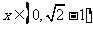 ;
;
(2) .此时
.此时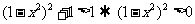 .此式恒成立.综合得:
.此式恒成立.综合得:
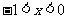 ;
;
(3)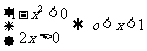 .此时
.此时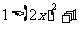 .此式恒不成立;
.此式恒不成立;
(4)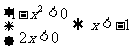 ,此时1>1恒不成立.
,此时1>1恒不成立.
综合(1),(2),(3),(4)得满足不等式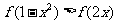 的x的范围是
的x的范围是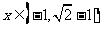
9.在平面直角坐标系xOy中,已知圆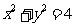
上有且仅有四个点到直线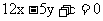 的距离为1,
的距离为1,
则实数c的取值范围是______▲_____
[分析]本题考查直线与圆的位置关系,是一道若数形结合的
好题,解法简单,是一道中等偏易的题.
[解析]原点到此直线的距离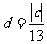 .为使圆上有且仅有4点与该直线距离为1,必须
.为使圆上有且仅有4点与该直线距离为1,必须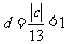 得
得
注意:在某些网站上流传的本题答案为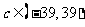 ,显然是错误的答案.
,显然是错误的答案.
8.函数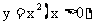 y的图像在点
y的图像在点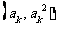 处的切线与x轴交点的横坐标为
处的切线与x轴交点的横坐标为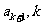 为正整数,a1=16,则
为正整数,a1=16,则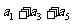 =____▲_____
=____▲_____
[分析]本题至多只能算一道中等题.又是一道区分度较大的好题.即使差生也能够通过列解方程的方法,逐一求出各项然后求和. 可是那样付出的代价可太高了.较好的方法是:
[解析]由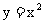 得
得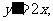 y的图像在点
y的图像在点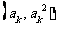 处的切线
处的切线
斜率为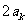 ,切线方程是:
,切线方程是:  .令y=0,得
.令y=0,得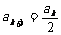 .于是这个数列的前5项为:
.于是这个数列的前5项为:
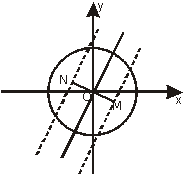 16,8,4,2,1.故
16,8,4,2,1.故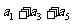 =16+4+1=21.
=16+4+1=21.
7.下图是一个算法的流程图,则输出S的值是______▲_______
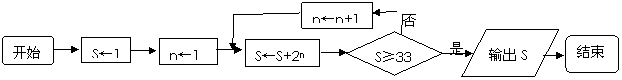
[分析]框图反映的是计算机运算程序,时代信息很强,所以是课改地区的必考内容.但即使是非课改地区,只要能够读懂题意,还是有办法解出来的.至多只能算一道中等题.
[解析1]初始值S=1.第1次操作:令n=1,得S1=1+21=3.显然3<33;
第2次操作:令n=2,得S2=3+22=7.显然7<33;
第3次操作:令n=3,得S3=7+23=15.显然15<33;
第4次操作:令n=4,得S4=15+24=31.显然31<33;
第5次操作:令n=5,得S5=15+25=63.符合63≥33.于是输出63,操作结束.
这就是说,最后输出的s值是63.
[解析2]将本题中的程序语言翻译成数学语言:等比数列的首项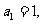 公比
公比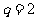 ,求满足
,求满足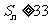 的最小值
的最小值 .由于
.由于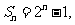 令
令 得
得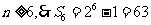
6.在平面直角坐标系xOy中,双曲线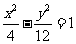 上一点M,点M的横坐标是3,则M到双曲线右焦点的距离是___▲_______
上一点M,点M的横坐标是3,则M到双曲线右焦点的距离是___▲_______
[分析]解本题只需掌握圆锥曲线的第二定义,还是容易题.
[解析]此双曲线的半焦距为4,离心率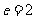 .设双曲线的右焦点为F.∵右准线为
.设双曲线的右焦点为F.∵右准线为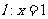
故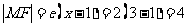
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com