
5、DNA与RNA分类的主要依据是( )
A、空间结构的不同 B、所含磷酸不同
C、所含五碳糖不同 D、在细胞中存在的部位不同
4、一条肽链的分子式C22H34O13N6,其水解后共产生了下列3种氨基酸( )
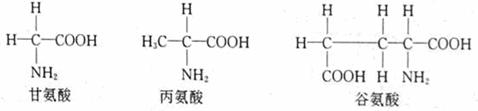
据此判断,下列有关叙述错误的是[( )
A、在细胞中合成C22H34O13N6分子需要有核糖体
B、合成1个C22H34O13N6分子同时将产生5个水分子
C、1个C22H34O13N6分子中存在1个游离的氨基和3个游离的羧基
D、1个C22H34O13N6分子水解后可以产生3个谷氨酸
3、据报道:非洲毒蛇(眼镜蛇)产生的毒素为一种环状十二肽,若氨基酸的平均分子量为a,则该毒素的相对分子质量约为( )
A、12a-12×18 B、12a-11×18 C、 11a-12×18 D、12a-10×18
2、现有氨基酸800个,其中氨基总数为810个,羧基总数为808个,则由这些氨基酸合成的含有2条肽链的蛋白质共有肽键、氨基和羧基的数目依次分别为( )
A、798、2和2 B、798、12和10 C、799、1和1 D、799、11和9
1、某学者正在研究某一种鸟类的季节性迁徙行为,他的研究对象属于哪一生命层次( )
A、个体 B、种群 C、生物群落 D、生态系统
(17)(本小题满分12分)
已知函数 (
( )的最小正周期为
)的最小正周期为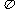 ,
,
(Ⅰ)求 的值;
的值;
(Ⅱ)将函数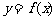 的图像上各点的横坐标缩短到原来的
的图像上各点的横坐标缩短到原来的 ,纵坐标不变,得到
,纵坐标不变,得到
函数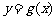 的图像,求函数
的图像,求函数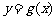 在区间
在区间 上的最小值.
上的最小值.
[命题意图]本小题主要考察综合运用三角函数公式、三角函数的性质,进行运算、变形、转换和求解的能力。
[解析]

因此 1 g(x)
g(x)
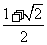 ,故 g(x)在此区间内的最小值为1.
,故 g(x)在此区间内的最小值为1.
(18)(本小题满分12分)
已知等差数列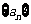 满足:
满足: ,
,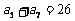 .
.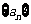 的前n项和为
的前n项和为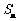 .
.
(Ⅰ)求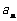 及
及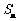 ;(Ⅱ)令
;(Ⅱ)令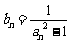 (
( ),求数列
),求数列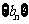 的前n项和
的前n项和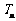 .
.
[命题意图]本题考查等差数列的通项公式与前n项和公式的应用、裂项法求数列的和,熟练数列的基础知识是解答好本类题目的关键。
[解析](Ⅰ)设等差数列 的公差为d,因为
的公差为d,因为 ,
, ,所以有
,所以有
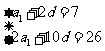 ,解得
,解得 ,
,
所以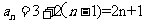 ;
;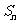 =
=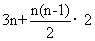 =
=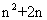 。
。
(Ⅱ)由(Ⅰ)知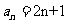 ,所以bn=
,所以bn=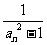 =
=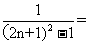
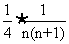 =
=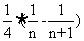 ,
,
所以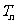 =
= =
=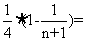
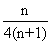 ,
,
即数列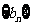 的前n项和
的前n项和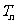 =
=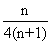 。
。
(19)(本小题满分12分)
一个袋中装有四个形状大小完全相同的球,球的编号分别为1,2,3,4.
(Ⅰ)从袋中随机抽取两个球,求取出的球的编号之和不大于4的概率;
(Ⅱ)先从袋中随机取一个球,该球的编号为m,将球放回袋中,然后再从袋中随机取一个球,该球的编号为n,求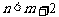 的概率.
的概率.
[命题意图]本小题主要考察古典概念、对立事件的概率计算,考察学生分析问题 、解决问题的能力。
、解决问题的能力。
[解析](I)从袋子中随机取两个球,其一切可能的结果组成的基本事件有1和2,1和3,1和4,2和3,2和4,3和4,共6个。
从袋中随机取出的球的编号之和不大于4的事件共有1和2,1和3两个。
因此所求事件的概率为1/3。
(II)先从袋中随机取一个球,记下编号为m,放回后,在从袋中随机取一个球,记下编号为n,其一切可能的结果(m, n)有:
(1,1)(1,2),(1,3),(1,4),(2,1),(2,2),(2,3),(2,4),(3,1)(3,2), (3,3) (3,4),(4,1) (4,2),(4,3)(4,4),共16个
有满足条件n≥ m+2 的事件为(1,3) (1,4) (2,4),共3个
所以满足条件n ≥ m+2 的事件的概率为 P=3/16
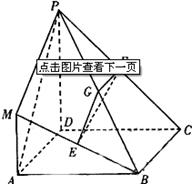 故满足条件n<m+2 的事件的概率为
故满足条件n<m+2 的事件的概率为 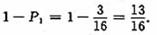
(20)(本小题满分12分)
在如图所示的几何体中,四边形 是正方形,
是正方形,
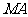
 平面
平面 ,
,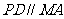 ,
,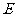 、
、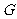 、
、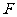 分别为
分别为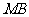 、
、 、
、 的中点,且
的中点,且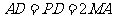 .
.
(I)求证:平面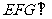 平面
平面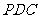 ;
;
(II)求三棱锥 与四棱锥
与四棱锥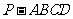 的体积
的体积
之比.
[命题意图]本小题主要考查空间中的线面关系,考查线面垂直、面面垂直的判定及几何体体积的计算,考查试图能力和逻辑思维能力。
[解析](I) 证明:由已知MA 平面ABCD,PD ∥MA,
证明:由已知MA 平面ABCD,PD ∥MA,
所以 PD∈平面ABCD
又 BC ∈ 平面ABCD,
因为 四边形ABCD为正方形,
所以 PD⊥ BC
又 PD∩DC=D,
因此 BC⊥平面PDC
在△PBC中,因为G平分为PC的中点,
所以 GF∥BC
因此 GF⊥平面PDC
又  GF ∈平面EFG,
GF ∈平面EFG,
所以 平面EFG⊥平面PDC.
(Ⅱ )解:因为PD⊥平面ABCD,四边形ABCD为正方形,不妨设MA=1,
则 PD=AD=2,AB CD
CD
所以 Vp-ABCD=1/3S正方形ABCD,PD=8/3
由于 DA⊥面MAB的距离
所以 DA即为点P到平面MAB的距离,
三棱锥 Vp-MAB=1/3×1/2×1×2×2=2/3,所以 Vp-MAB:Vp-ABCD=1:4。
(21)(本小题满分12分)
已知函数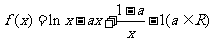
(I)当 时,求曲线
时,求曲线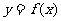 在点
在点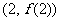 处的切线方程;
处的切线方程;
(II)当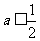 时,讨论
时,讨论 的单调性.
的单调性.
[命题意图]本小题主要考查导数的概念、导数的几何意义和利用导数研究函数性质的能力,考查分类讨论思想、数形 结合思想和等价变换思想。
结合思想和等价变换思想。
[解析]解:(Ⅰ) 当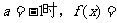

所以 
因此,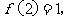
即 曲线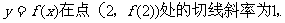 ……………………
……………………
又 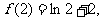
所以曲线
(Ⅱ)因为  ,
,
所以 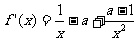
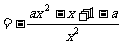
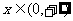 ,
,
 令
令 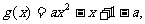

(1) 当a=0时,g(x)=-x+1,x∈(0,+∞),
所以 当x∈(0,1)时,g(x)>0,此时f(x)<0,函数f(x)单调递减
(2)
当a≠0时,由 f(x)=0,
f(x)=0,
即 ax2-x+1=0, 解得 x1=1,x2=1/a-1
① 当a=1/2时,x1= x2, g(x)≥0恒成立,此时f(x)≤0,函数f(x)在(0,+∞)上单调递减;
② 当0<a<1/2时,1/2-1>1>0
x∈(0,1)时,g(x)>0,此时f(x)<0,函数f(x)单调递减
x∈(1,1/a-1)时,g(x)>0,此时f(x)<o,函数f(x)单调递减
x∈(1/a-1,+∞)时,g(x )>0,此时f(x)<o,函数f(x)单调递减
)>0,此时f(x)<o,函数f(x)单调递减
③ 当a<0时,由于1/a-1<0,
x∈(0,1)时,g(x)>0,此时f,(x)<0函数f(x)单调递减;
x∈(1 ,∞)时,g(x)<0此时函数f,(x)<0单调递增。
综上所述:
当a≤ 0 时,函数f(x)在(0,1)上单调递减;
函数f(x)在 (1, +∞) 上单调递增
当a=1/2时,函数f(x)在(0, + ∞)上单调递减
当0<a<1/2时,函数f(x)在(0,1)上单调递减;
函数 f(x)在(1,1/a -1)上单调递增;
函数f(x)在(1/a,+ ∞)上单调递减。
(22)(本小题满分14分)
 如图,已知椭圆
如图,已知椭圆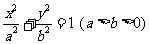 过点.
过点.
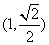 ,离心率为
,离心率为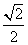 ,左、右焦点分别为
,左、右焦点分别为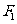 、
、
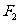 .点
.点 为直线
为直线 上且不在
上且不在 轴上的任意
轴上的任意
一点,直线 和
和 与椭圆的交点分别为
与椭圆的交点分别为 、
、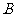
和 、
、 ,
,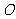 为坐标原点.
为坐标原点.
(I)求椭圆的标准方程;
(II)设直线 、
、 的斜线分别为
的斜线分别为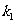 、
、 .
.
(i)证明: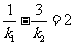 ;
;
(ii)问直线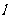 上是否存在点
上是否存在点 ,使得直线
,使得直线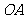 、
、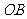 、
、 、
、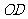 的斜率
的斜率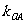 、
、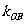 、
、 、
、 满足
满足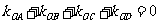 ?若存在,求出所有满足条件的点
?若存在,求出所有满足条件的点 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
[命题意图]本小题主要考查椭圆的基本概念和性质,考查直线与椭圆的位置关系,考查数形结合思想、分类讨论思想以及探求解决新问题的能力。
[解析](Ⅰ)解:因为椭圆过点(1,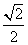 ),e=
),e=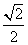 ,
,
所以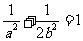 ,
,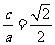 .
.
又a2=b2+c2,
所以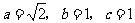 ,故所求椭圆方程为
,故所求椭圆方程为 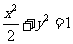 .
.
(Ⅱ)(i)设点P(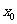 ,
, ),则
),则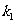 =
=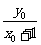 ,
, =
=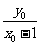 ,因为点
,因为点 不在
不在 轴上,所以
轴上,所以
 ,又
,又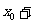
 =2,所以
=2,所以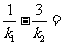
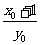
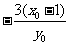 =
=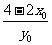
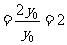 ,
,
因此结论成立。


(13)执行右图所示的程序框图,若输入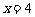 ,则输出y的值为
.
,则输出y的值为
.
[答案]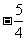
[解析]当x=4时,y=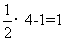 ,此时|y-x|=3;当x=1时,y=
,此时|y-x|=3;当x=1时,y=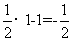 ,此时|y-x|=
,此时|y-x|=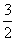 ;
;
当x= 时,y=
时,y= ,此时|y-x|=
,此时|y-x|=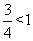 ,故输出y的值为
,故输出y的值为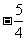 。
。
[命题意图]本题考查程序框图的基础知识,考查了同学们的试图能力。
(14)已知 ,且满足
,且满足 ,则xy的最大值为
.
,则xy的最大值为
.
[答案]3
[解析]
[命题意图]
(15) 在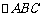 中,角A,B,C所对的边分别为a,b,c,若
中,角A,B,C所对的边分别为a,b,c,若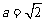 ,
,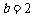 ,
,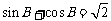 ,则角A的大小为
.
,则角A的大小为
.
[答案]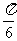
[解析]由 得
得 ,即
,即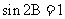 ,因为
,因为 ,所以
,所以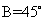 ,又因为
,又因为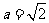 ,
,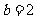 ,所以在
,所以在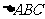 中,由正弦定理得:
中,由正弦定理得: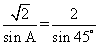 ,解得
,解得 ,又
,又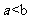 ,所以
,所以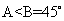 ,所以
,所以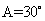 。
。
[命题意图]本题考查了三角恒等变换、已知三角函数值求解以及正弦定理,考查了同学们解决三角形问题的能力,属于中档题。
(16) 已知圆C过点(1,0),且圆心在x轴的正半轴上,直线l: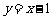 被该圆所截得
被该圆所截得
的弦长为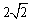 ,则圆C的标准方程为
.
,则圆C的标准方程为
.
[答案]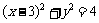
[解析]由题意,设圆心坐标为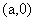 ,则由直线l:
,则由直线l: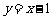 被该圆所截得
被该圆所截得
的弦长为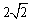 得,
得,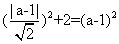 ,解得
,解得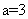 或-1,又因为圆心在x轴的正半轴上,所以
或-1,又因为圆心在x轴的正半轴上,所以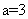 ,故圆心坐标为(3,0),又已知圆C过点(1,0),所以所求圆的半径为2,故圆C的标准方程为
,故圆心坐标为(3,0),又已知圆C过点(1,0),所以所求圆的半径为2,故圆C的标准方程为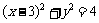 。
。
[命题意图]本题考查了直线的方程、点到直线的距离、直线与圆的关系,考查了同学们解决直线与圆问题的能力。
(1) 已知全集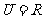 ,集合
,集合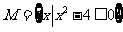 ,则
,则 =
=
A. 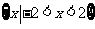 B.
B. 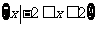
C. D.
D. 
[答案]C
[解析]因为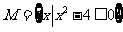
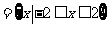 ,全集
,全集 ,
,
所以
 ,故选C。
,故选C。
[命题意图]本题考查集合的补集运算、二次不等式的解法等基础知识,属基础题。
(2)已知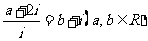 ,其中
,其中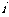 为虚数单位,则
为虚数单位,则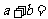
A. 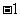 B.
1
C. 2
D. 3
B.
1
C. 2
D. 3
[答案]B
[解析]由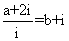 得
得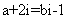 ,所以由复数相等的意义知:
,所以由复数相等的意义知: ,所以
,所以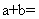 1,故选B.
1,故选B.
[命题意图]本题考查复数相等的意义、复数的基本运算,属保分题。
(3)函数 的值域为
的值域为
A. 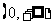 B.
B.  C.
C. 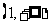 D.
D.

[答案]A
[解析]因为 ,所以
,所以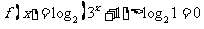 ,故选A。
,故选A。
[命题意图]本题考查对数函数的单调性、函数值域的求法等基础知识。
(4)在空间,下列命题正确的是
A.平行直线的平行投影重合
B.平行于同一直线的两个平面平行
C.垂直于同一平面的两个平面平行
D.垂直于同一平面的两条直线平行
[答案]D
[解析]由空间直线与平面的位置关系及线面垂直与平行的判定与性质定理可以很容易得出答案。
[命题意图]本题考查空间直线与平面的位置关系及线面垂直与平行的判定与性质,属基础题。
(5)设 为定义在
为定义在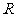 上的奇函数,当
上的奇函数,当 时,
时,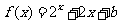 (
( 为常数),则
为常数),则
(A)-3 (B)-1 (C)1 (D)3
[答案]A
[解析]因为 为定义在R上的奇函数,所以有
为定义在R上的奇函数,所以有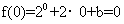 ,解得
,解得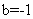 ,所以
,所以
当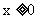 时,
时,  ,即
,即
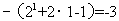 ,故选D.
,故选D.
[命题意图]本题考查函数的基本性质,熟练函数的基础知识是解答好本题的关键.
(6)在某项体育比赛中,七位裁判为一选手打出的分数如下:
90 89 90 95 93 94 93
去掉一个最高分和一个最低分后,所剩数据的平均值和方差分别为
(A)92 , 2 (B) 92 , 2.8
(C) 93 , 2 (D) 93 , 2.8
[答案]B
[解析]由题意知,所剩数据为90,90,93,94,93,所以其平均值为
90+ =92;方差为
=92;方差为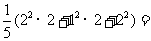 2.8,故选B。
2.8,故选B。
[命题意图]本题考查平均数与方差的求法,属基础题。
(7)设 是首项大于零的等比数列,则“
是首项大于零的等比数列,则“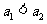 ”是“数列
”是“数列 是递增数列”的
是递增数列”的
(A)充分而不必要条件 (B)必要而不充分条件
(C)充分必要条件 (D)既不充分也不必要条件
[答案]C
[解析]若已知 ,则设数列
,则设数列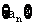 的公比为
的公比为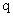 ,因为
,因为 ,所以有
,所以有 ,解得
,解得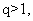 又
又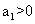 ,所以数列
,所以数列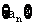 是递增数列;反之,若数列
是递增数列;反之,若数列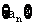 是递增数列,则公比
是递增数列,则公比 且
且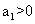 ,所以
,所以 ,即
,即 ,所以
,所以 是数列
是数列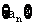 是递增数列的充分必要条件。
是递增数列的充分必要条件。
[命题意图]本题考查等比数列及充分必要条件的基础知识,属保分题。
(8)已知某生产厂家的年利润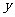 (单位:万元)与年产量
(单位:万元)与年产量 (单位:万件)的函数关系式为
(单位:万件)的函数关系式为 ,则使该生产厂家获得最大年利润的年产量为
,则使该生产厂家获得最大年利润的年产量为
(A)13万件 (B)11万件
(C) 9万件 (D)7万件
[答案]C
[解析]令导数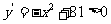 ,解得
,解得 ;令导数
;令导数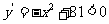 ,解得
,解得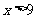 ,所以函数
,所以函数 在区间
在区间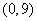 上是增函数,在区间
上是增函数,在区间 上是减函数,所以在
上是减函数,所以在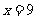 处取极大值,也是最大值,故选C。
处取极大值,也是最大值,故选C。
[命题意图]本题考查导数在实际问题中的应用,属基础题。
(9)已知抛物线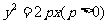 ,过其焦点且斜率为1的直线交抛物线与
,过其焦点且斜率为1的直线交抛物线与 、
、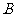 两点,若线段
两点,若线段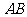 的中点的纵坐标为2,则该抛物线的准线方程为
的中点的纵坐标为2,则该抛物线的准线方程为
(A)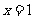 (B)
(B)
(C)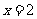 (D)
(D)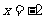
[答案]B
[解析]设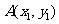 、
、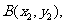 则有
则有 ,
, ,两式相减得:
,两式相减得:
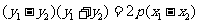 ,又因为直线的斜率为1,所以
,又因为直线的斜率为1,所以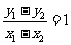 ,所以有
,所以有
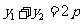 ,又线段
,又线段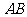 的中点的纵坐标为2,即
的中点的纵坐标为2,即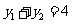 ,所以
,所以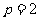 ,所以抛物线的准线方程为
,所以抛物线的准线方程为 。
。
[命题意图]本题考查抛物线的几何性质、直线与抛物线的位置关系等基础知识,
(10)观察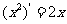 ,
,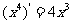 ,
, ,由归纳推理可得:若定义在
,由归纳推理可得:若定义在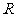 上的函数
上的函数 满足
满足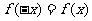 ,记
,记 为
为 的导函数,则
的导函数,则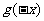 =
=
(A) (B)
(B)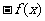 (C)
(C)  (D)
(D)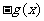
[答案]D
[解析]由给出的例子可以归纳推理得出:若函数 是偶函数,则它的导函数是奇函数,因为定义在
是偶函数,则它的导函数是奇函数,因为定义在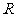 上的函数
上的函数 满足
满足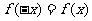 ,即函数
,即函数 是偶函数,所以它的导函数是奇函数,即有
是偶函数,所以它的导函数是奇函数,即有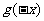 =
=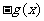 ,故选D。
,故选D。
[命题意图]本题考查函数、归纳推理等基础知识,考查同学们类比归纳的能力。
(11)函数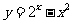 的图像大致是
的图像大致是
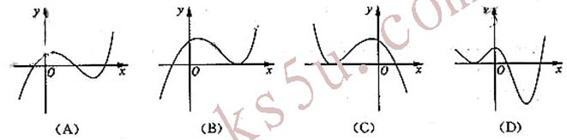
[答案]A
[解析]因为当x=2或4时,2x
 -
- =0,所以排除B、C;当x=-2时,2x
=0,所以排除B、C;当x=-2时,2x
 -
- =
=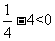 ,故排除D,所以选A。
,故排除D,所以选A。
[命题意图]本题考查函数的图象,考查同学们对函数基础知识的把握程度以及数形结合的思维能力。
(12)定义平面向量之间的一种运算“ ”如下:对任意的
”如下:对任意的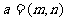 ,
,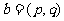 ,令
,令 ,下面说法错误的是
,下面说法错误的是
(A)若a与b共线,则
(B)
(C)对任意的 ,有
,有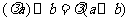
(D)
[答案]B
[解析]若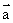 与
与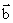 共线,则有
共线,则有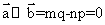 ,故A正确;因为
,故A正确;因为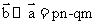 ,而
,而
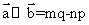 ,所以有
,所以有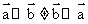 ,故选项B错误,故选B。
,故选项B错误,故选B。
[命题意图]本题在平面向量的基础上,加以创新,属创新题型,考查平面向量的基础知识以及分析问题、解决问题的能力。
第三节 书面表达(满分30分)
假设你是李华,你的美国笔友Peter曾表示希望来中国教书。你校现需招聘外教,请给他写封信,告知招聘信息。内容主要包括:
1. 教授课程:英语口语、英语写作、今日美国、今日英国等
2. 授课对象:高中生(至少三年英语基础)
3. 工作量:
--每周12学时,任先三门课
--担任学生英语俱乐部或英语校报顾问(advisor)
注意:
a) 词数100左右;
b) 可以适当增加细节,以使行文连贯;
c) 开关语已为你写好,请将完整的回信书写在答题卡上。
Dear Peter,
I remember you told me you were interested in teaching in China.
Best,
Li Hua
One possible version
Dear Peter,
I remember you told me you were interested in teaching in China. Our school now is looking for a native-speaker to teach some courses to senior high students. If you come, you can choose three of the following four courses: Speaking, Writing, Britain Today and America Today, and teach 12 hours a week. The students who are going to take these courses have at least three years of English learning experiences. Besides teaching, you will also work as an advisor to our students’ English club or our school’s English newspaper.
Please let me know if you are interested and if you have any other questions. I’d be more than happy to help.
Best,
Li Hua
第二节 短文改错(共10小题;每小题1.5分,满分15分)
此题要求改正所给短文中的错误。对标有题号的第一行作出判断:如无错误,在答题卡相应的的位置上画一个勾(√);如有错误(每行只有一个错误),则按下列情况改正:
此行多一个词:把多余的词在答题卡相应的位置上用斜线(\)划掉。
此行缺一个词:在答题卡相应的位置上写出该加的词,并附带前(后)词。
此行错一个词:在答题卡相应的位置上写出该该错和改正后的词。
注意:原行没有错的不要改。
Christie was one of my best friend at high school 76
At that time, we often spend time together. 77
Thank to her help, I made great progress in my 78
study. Last year, she decided to study abroad. In 79
other words, we would be separated for long time. 80
Before her leaving off, I prepared a gift to show 81
my best whishes to him. She said it was the best 82
gift she has ever had. From then on, we’ve 83
kept touch with another through e-mails. I 84
look forward to see her again in the near future. 85
答案:
76. friend → friends. one of 后接名词复数
77. spend →spent. At that time表示过去发生的事情
78. Thank →Thanks. Thanks to 是固定短语,“多亏了,因为”
79. √
80. for a long. For a long time表示“一段时间”,固定短语
81. 去掉off. leave 已经表示离开之意,off多余
82. him →her. 代词使用要一致。
83. has →had.时态错误,应为过去完成时。
84. kept ∧in touch 固定短语keep in touch with表示“与人保持联系”
85. see →seeing. look forward to中的to是介词,后接动词时要用动名词形式。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com