
1.下列不属于下丘脑功能的是 ( )
A.具有体温调节中枢,可以维持体温的相对稳定
B.能产生促甲状腺激素释放激素、生长激素等多种激素
C.能传导兴奋,并能控制生物节律
D.具有渗透压感受器,能感受细胞外液渗透压的变化
21.已知等比数列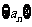 的首项为
的首项为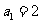 ,公比为
,公比为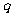 (
(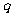 为正整数),且满足
为正整数),且满足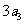 是
是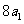 与
与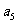 的等差中项;数列
的等差中项;数列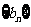 满足
满足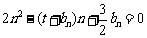 (
(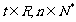 ).
).
(1)求数列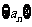 的通项公式;
的通项公式;
(2)试确定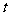 的值,使得数列
的值,使得数列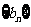 为等差数列;
为等差数列;
(3)当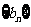 为等差数列时,对任意正整数
为等差数列时,对任意正整数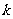 ,在
,在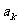 与
与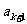 之间插入2共
之间插入2共 个,得到一个新数列
个,得到一个新数列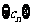 .设
.设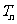 是数列
是数列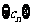 的前
的前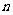 项和,试求满足
项和,试求满足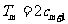 的所有正整数
的所有正整数 的值。
的值。
20.在直角坐标系xOy中,椭圆C1: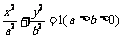 的左、右焦点分别为F1、F2,其中右焦点F2也是拋物线C2:y2 = 4x的焦点,点M为C1与C2在第一象限的交点,且|MF2|
=
的左、右焦点分别为F1、F2,其中右焦点F2也是拋物线C2:y2 = 4x的焦点,点M为C1与C2在第一象限的交点,且|MF2|
= 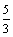 .
.
(1)求椭圆C1的方程;
(2)设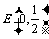 ,是否存在斜率为k (k≠0)的直线l与椭圆C1交于A、B两点,且|AE| = |BE|?若存在,求k的取值范围;若不存在,请说明理由.
,是否存在斜率为k (k≠0)的直线l与椭圆C1交于A、B两点,且|AE| = |BE|?若存在,求k的取值范围;若不存在,请说明理由.
19.某电视生产企业有A、B两种型号的电视机参加家电下乡活动,若企业投放A、B两种型号电视机的价值分别为a、b万元,则农民购买电视机获得的补贴分别为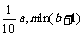 万元(m>0且为常数).已知该企业投放总价值为10万元的A、B两种型号的电视机,且A、B两种型号的投放金额都不低于1万元.
万元(m>0且为常数).已知该企业投放总价值为10万元的A、B两种型号的电视机,且A、B两种型号的投放金额都不低于1万元.
(1)请你选择自变量,将这次活动中农民得到的总补贴表示为它的函数,并求其定义域;
(2)求当投放B型电视机的金额为多少万元时,农民得到的总补贴最大?
18.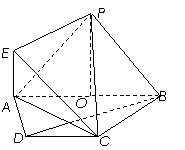 如图,在等腰梯形ABCD中,AB∥DC,AB = 4,CD = 2,等腰梯形的高为3,O为AB中点,PO⊥平面ABCD,垂足为O,PO = 2,EA∥PO.
如图,在等腰梯形ABCD中,AB∥DC,AB = 4,CD = 2,等腰梯形的高为3,O为AB中点,PO⊥平面ABCD,垂足为O,PO = 2,EA∥PO.
(1)求证:BD⊥平面EAC;
(2)求二面角E-AC-P的平面角的余弦值.
17. “上海世博会”将于2010年5月1日至10月31日在上海举行。世博会“中国馆·贵宾厅”作为接待中外贵宾的重要场所,其中陈列的艺术品是体现兼容并蓄、海纳百川的重要文化载体,为此,上海世博会事物协调局将举办“中国2010年上海世博会‘中国馆·贵宾厅’艺术品方案征集”活动.某地美术馆从馆藏的中国画、书法、油画、陶艺作品中各选一件代表作参与应征,假设这四件代表作中中国画、书法、油画入选“中国馆·贵宾厅”的概率均为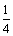 ,陶艺入选“中国馆·贵宾厅”的概率为
,陶艺入选“中国馆·贵宾厅”的概率为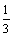 .假定这四件作品是否入选相互没有影响.
.假定这四件作品是否入选相互没有影响.
(1)求该地美术馆选送的四件代表作中恰有一件作品入选“中国馆·贵宾厅”的概率;
(2)设该地美术馆选送的四件代表作中入选“中国馆·贵宾厅”的作品件数为随机变量 ,求
,求 的数学期望.
的数学期望.
16.已知向量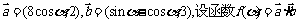 .
.
(1)求函数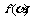 的最大值;
的最大值;
(2)在锐角三角形ABC中,角A、B、C的对边分别为a、b、c,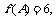 且△ABC的面积为3,
且△ABC的面积为3,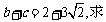 a的值.
a的值.
15.给定项数为m (m∈N*,m≥3)的数列{an},其中ai∈{0,1}(i= 1,2,3,…,m),这样的数列叫”0-1数列”.若存在一个正整数k (2≤k≤m – 1),使得数列{an}中某连续k项与该数列中另一个连续k项恰好按次序对应相等,则称数列{an}是“k阶可重复数列”.例如数列{an}:0,1,1,0,1,1,0,因为a1,a2,a3,a4与a4,a5,a6,a7按次序对应相等,所以数列{an}是“4阶可重复数列”.
(1)已知数列{bn}:0,0,0,1,1,0,0,1,1,0,则该数列 “5阶可重复数列”(填“是”或“不是”);
(2)要使项数为m的所有”0-1数列”都为 “2阶可重复数列”,则m的最小值是 .
14.已知函数f (x) = 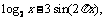 则函数y = f (|x|)的零点个数为
.
则函数y = f (|x|)的零点个数为
.
13.某研究机构为了研究人脚的大小与身高之间的关系,随机抽测了105人,并规定:身高大于175cm的为“高个”,小于或等于175cm的为“非高个”;脚长大于42码的为“大脚”,小于或等于42码的为“非大脚”.根据测得结果得到一个2×2列联表.根据该表信息,能够以 的把握认为“脚的大小与身高有关系”.(填百分比).
|
|
高 个 |
非高个 |
总 计 |
|
大 脚 |
20 |
30 |
50 |
|
非大脚 |
10 |
45 |
55 |
|
总 计 |
30 |
75 |
105 |
附: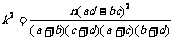 ,其中n = a + b + c
+ d.
,其中n = a + b + c
+ d.
|
P (k2≥k0) |
0.05 |
0.025[ |
0.010[ |
|
k0 |
3.841 |
5.024 |
6.635 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com