
7.质量为m的球A以速率v与质量为3m的静止球B沿光滑水平面发生正碰,碰撞后A球速率为v/2,则B球速率可能为
A.v/6 B.v/3 C.v/2 D.2v
6.从离地面相同的高度以相同的初速率抛出质量相同的甲、乙两球,甲球竖直上抛,乙球竖直下抛,不计空气阻力,两球最后都落在地面上,此过程中,以下说法正确的是
A 两球的动量变化量及落地时的动量均相同
B 两球的动量变化量及落地时的动量均不相同
C. 两球的动量变化量不相同,但落地时的动量相同
D.两球的动量变化量相同,但落地时的动量不相同
5.下列几种现象中,动量不守恒的是
A.在光滑水平面上两球发生碰撞
B.车原来静止在光滑的水平面上,车上的人从车头走到车尾
C.水平放置的弹簧一端固定,另一端与置于光滑水平面的物体相连,伸长的弹簧拉物体运动
D.火箭的反冲运动
4.玻璃杯从同一高度落下,掉在石头上比掉在草地上容易碎,这是由于玻璃杯与石头的撞击过程中
A 玻璃杯的动量较大 B 玻璃杯受到的冲量较大
C 玻璃杯的动量变化较大 D 玻璃杯的动量变化较快
3.几个力作用到物体上,关于其中一个力F的冲量的方向,下列说法中正确的是
A.与物体动量的方向相同
B.与力F的方向相同
C.与物体动量变化的方向相同
D.与物体速度变化的方向相同
2.两个物体具有相同的动量,则它们一定具有
A.相同的速度 B.相同的质量
C.相同的运动方向 D.相同的加速度
1.下列说法中正确的是
A.物体的动量变化,其速度大小一定变化
B.物体的动量变化,其速度方向一定变化
C.物体的动量变化,其动能一定变化
D.物体的速率变化,其动量一定变化
(17)(本小题满分12分)
已知函数 ,其图象过点(
,其图象过点( ,
, ).
).
(Ⅰ)求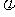 的值;
的值;
(Ⅱ)将函数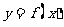 的图象上各点的横坐标缩短到原来的
的图象上各点的横坐标缩短到原来的 ,纵坐标不变,得到函数
,纵坐标不变,得到函数 的图象,求函数
的图象,求函数 在[0,
在[0,  ]上的最大值和最小值.
]上的最大值和最小值.
[解析](Ⅰ)因为已知函数图象过点( ,
, ),所以有
),所以有

 ,即有
,即有
 =
= ,所以
,所以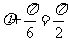 ,解得
,解得 。
。
(Ⅱ)由(Ⅰ)知 ,所以
,所以
= =
=
 ,
,
所以 =
= ,因为x
,因为x [0,
[0,  ],所以
],所以
 ,
,
所以当 时,
时, 取最大值
取最大值 ;当
;当
 时,
时, 取最小值
取最小值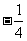 。
。
[命题意图]本题考查三角函数的诱导公式及二倍角等基本公式的灵活应用、图象变换以及三角函数的最值问题、分析问题与解决问题的能力。
(18)(本小题满分12分)
已知等差数列 满足:
满足: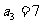 ,
, ,
, 的前n项和为
的前n项和为 .
.
(Ⅰ)求 及
及 ;
;
(Ⅱ)令bn= (n
(n N*),求数列
N*),求数列 的前n项和
的前n项和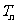 .
.
[解析](Ⅰ)设等差数列 的公差为d,因为
的公差为d,因为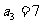 ,
, ,所以有
,所以有
 ,解得
,解得 ,
,
所以 ;
; =
= =
=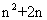 。
。
(Ⅱ)由(Ⅰ)知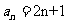 ,所以bn=
,所以bn= =
=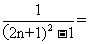
 =
= ,
,
所以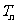 =
= =
=
 ,
,
即数列 的前n项和
的前n项和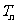 =
= 。
。
[命题意图]本题考查等差数列的通项公式与前n项和公式的应用、裂项法求数列的和,熟练数列的基础知识是解答好本类题目的关键。
 (19)(本小题满分12分)
(19)(本小题满分12分)
如图,在五棱锥P—ABCDE中,PA⊥平面ABCDE,AB∥CD,AC∥ED,AE∥BC,  ABC=45°,AB=2
ABC=45°,AB=2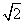 ,BC=2AE=4,三角形PAB是等腰三角形.
,BC=2AE=4,三角形PAB是等腰三角形.
(Ⅰ)求证 :平面PCD⊥平面PAC;
:平面PCD⊥平面PAC;
(Ⅱ)求直线PB与平面PCD所成角的大小;
(Ⅲ)求四棱锥 P—ACDE的体积.
P—ACDE的体积.
[解析](Ⅰ)证明:因为 ABC=45°,AB=2
ABC=45°,AB=2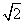 ,BC=4,所以在
,BC=4,所以在 中,由余弦定理得:
中,由余弦定理得: ,解得
,解得 ,
,
所以 ,即
,即 ,又PA⊥平面ABCDE,所以PA⊥
,又PA⊥平面ABCDE,所以PA⊥ ,
,
又PA ,所以
,所以 ,又AB∥CD,所以
,又AB∥CD,所以 ,又因为
,又因为
 ,所以平面PCD⊥平面PAC;
,所以平面PCD⊥平面PAC;
(Ⅱ)由(Ⅰ)知平面PCD⊥平面PAC,所以在平面PAC内,过点A作 于H,则
于H,则
 ,又AB∥CD,AB
,又AB∥CD,AB 平面
平面 内,所以AB平行于平面
内,所以AB平行于平面 ,所以点A到平面
,所以点A到平面 的距离等于点B到平面
的距离等于点B到平面 的距离,过点B作BO⊥平面
的距离,过点B作BO⊥平面 于点O,则
于点O,则 为所求角,且
为所求角,且 ,又容易求得
,又容易求得 ,所以
,所以 ,即
,即 =
=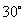 ,所以直线PB与平面PCD所成角的大小为
,所以直线PB与平面PCD所成角的大小为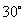 ;
;
(Ⅲ)由(Ⅰ)知 ,所以
,所以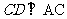 ,又AC∥ED,所以四边形ACDE是直角梯形,又容易求得
,又AC∥ED,所以四边形ACDE是直角梯形,又容易求得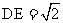 ,AC=
,AC=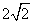 ,所以四边形ACDE的面积为
,所以四边形ACDE的面积为 ,所以
,所以
四棱锥 P—ACDE的体积为
P—ACDE的体积为 =
=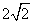 。
。
[命题意图]本题考查了空间几何体的的线面与面面垂直、线面角的求解以及几何体的体积计算问题,考查了同学们的空间想象能力以及空间思维能力。
(19)(标准答案) 本小题主要考察空间中的基本关系,考察线面垂直、面面垂直的判定以及线面角和集合体体积的计算,考查识图能力、空间想象力和逻辑推理能力,满分12分
(|)证明:
在△ABC中,因为∠ABC=45°,BC=4,AB= ,
,
所以AC2=AB+BC2 -2AB·BC·cos45°=8
-2AB·BC·cos45°=8
因此
AC= ,
,
故BC2=AC2+AB2,
所以∠BAC=90°----------------------------------------------------
又PA⊥平面ABCDE,AB∥CD,
所以CD⊥PA,CD⊥AC,
又 PA,AC  平面PAC,且PA
平面PAC,且PA AC
AC =A,
=A,
所以 CD⊥PAC,又 CD 平面PCD,
平面PCD,
所以 平面PCD⊥平面PAC--------------------------------------------

则 ,
,
又  ,
,
所以 
解法二:
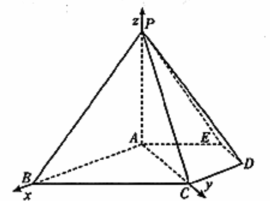
由(|)知AB,AC,AP两两相互垂直,分别以AB、AC、AP为x轴、y轴、z轴建立如图所示的空间直角坐标系,由于△PAB是等腰三角形,
 所以
PA=AB=
所以
PA=AB= ,
,
又AC= ,
,

所以 ,
,
因此直线 PB与平面PCD所成的角为
PB与平面PCD所成的角为
(Ⅲ)因为AC∥ED,CD⊥AC,
所以 四边形ACDE是直角梯形,
因为 AE=2,∠ABC=45°,AE∥BC,
所以 ∠BAE=135°,
因此 ∠CAE=45°,
故
CD=AE·sin45°==2× =
= ,
,
所以

又 PA⊥平面ABCDE,
所以 
(20)(本小题满分12分)
某学校举行知识竞赛,第一轮选拔共设有 四个问题,规则如下:
四个问题,规则如下:
① 每位参加者计分器的初始分均为10分,答对问题 分别加1分、2分、3分、6分,答错任一题减2分;
分别加1分、2分、3分、6分,答错任一题减2分;
② 每回答一题,计分器显示累计分数,当累计分数小于8分时,答题结束,淘汰出局;当累计分数大于或等于14分时,答题结束,进入下一轮;当答完四题,累计分数仍不足14分时,答题结束,淘汰出局,当累计分数大于或等于14分时,答题结束 ,进入下一轮;当答完四题,累计分数仍不足14分时,答题结束,淘汰出局;
,进入下一轮;当答完四题,累计分数仍不足14分时,答题结束,淘汰出局;
③ 每位参加者按问题 顺序作答,直至答题结束.
顺序作答,直至答题结束.
假设甲同学对问题 回答正确的概率依次为
回答正确的概率依次为 ,且各题回答正确与否相互之间没有影响.
,且各题回答正确与否相互之间没有影响.
(Ⅰ)求甲同学能进入下一轮的概率;
(Ⅱ)用 表示甲同学本轮答题结束时答题的个数,求
表示甲同学本轮答题结束时答题的个数,求 的分布列和数学的
的分布列和数学的 .
.
[解析]本小题主要考查离散型随机变量的分布列和数学期望,考查对立事件、独立事件的概率和求解方法,考查用概率知识解决实际问题的能力.
解:设 分别为第一、二、三、四个问题.用
分别为第一、二、三、四个问题.用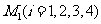 表示甲同学第
表示甲同学第 个问题回答正确,用
个问题回答正确,用 表示甲同学第
表示甲同学第 个问题回答错误,则
个问题回答错误,则 与
与 是对立事件
是对立事件 .由题意得
.由题意得

所以
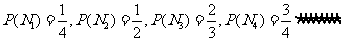
(Ⅰ)记“甲同学能进入下一轮”为事件 ,
,
则

(Ⅱ)由题意,随机变量 的可能取值为:
的可能取值为: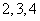 .
.
由于每题答题结果相互独立,
所以

因此
随机变量 的分布列为
的分布列为






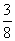
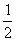
所以
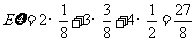 .
.
[命题意图]本题考查了相互独立事件同时发生的概率、考查了离散型随机变量的分布列以及数学期望的知识,考查了同学们利用所学知识解决实际问题的能力。
(21)(本小题满分12分)
如图,已知椭圆 的离心率为
的离心率为 ,以该椭圆上的点和椭圆的左、右焦点
,以该椭圆上的点和椭圆的左、右焦点 为顶点的三角形的周长为
为顶点的三角形的周长为
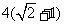 .一等轴双曲线的顶
.一等轴双曲线的顶 点是该椭圆的焦点,设
点是该椭圆的焦点,设 为该双曲线上异于顶点的任一点,直线
为该双曲线上异于顶点的任一点,直线 和
和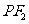 与椭圆的交点分别为
与椭圆的交点分别为 和
和 .
.

(Ⅰ)求椭圆和双曲线的标准方程;
(Ⅱ)设直线 、
、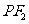 的斜率分别为
的斜率分别为 、
、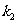 ,证明
,证明 ;
;
(Ⅲ)是否存在常数 ,使得
,使得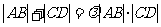 恒成立?若存在,求
恒成立?若存在,求 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
[解析](Ⅰ)由题意知,椭圆离心率为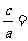
 ,得
,得 ,又
,又
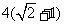 ,所以可解得
,所以可解得 ,
,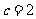 ,所以
,所以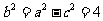 ,所以椭圆的标准方程为
,所以椭圆的标准方程为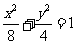 ;所以椭圆的焦点坐标为(
;所以椭圆的焦点坐标为( ,0),因为双曲线为等轴双曲线,且顶
,0),因为双曲线为等轴双曲线,且顶 点是该椭圆的焦点,所以该双曲线的标准方程为
点是该椭圆的焦点,所以该双曲线的标准方程为
 。
。
(Ⅱ)设点P( ,
, ),则
),则 =
= ,
,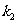 =
=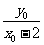 ,所以
,所以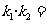

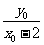 =
=
 ,又点P(
,又点P( ,
, )在双曲线上,所以有
)在双曲线上,所以有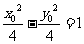 ,即
,即 ,所以
,所以
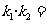
 =1。
=1。
(Ⅲ)假设存在常数 ,使得
,使得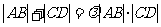 恒成立,则由(Ⅱ)知
恒成立,则由(Ⅱ)知 ,所以设直线AB的方程为
,所以设直线AB的方程为 ,则直线CD的方程为
,则直线CD的方程为 ,
,
由方程组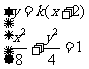 消y得:
消y得: ,设
,设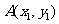 ,
, ,
,
则由韦达定理得:

所以|AB|=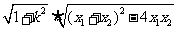 =
= ,同理可得
,同理可得
|CD|= =
= =
=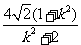 ,
,
又因为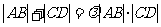 ,所以有
,所以有 =
= +
+
=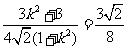 ,所以存在常数
,所以存在常数
 ,使得
,使得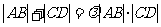 恒成立。
恒成立。
[命题意图]本题考查了椭圆的定义、离心率、椭圆与双曲线的标准方程、直线与圆锥曲线的位置关系,是一道综合性的试题,考查了学生综合运用知识解决问题的能力。其中问题(3)是一个开放性问题,考查了同学们观察、推理以及创造性地分析问题、解决问题的能力,
(标准答案)(21)本小题主要考查椭圆、双曲线的基本概念和基本性质。考查直线和椭圆的位置关系,考查坐标化、定值和存在性问题,考查数行结合思想和探求问题的能力。
解(Ⅰ)设椭圆的半焦距为c,由题意知:
 ,2a+2c=4(
,2a+2c=4(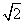 +1)
+1)
所以a=2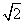 ,c=2,
,c=2,
又 =
= ,因此b=2。
,因此b=2。
故 椭圆的标准方程为
由题意设等轴双曲线的标准方程为
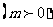 ,因为等轴双曲线的顶点是椭圆的焦点。
,因为等轴双曲线的顶点是椭圆的焦点。
所以m=2,
因此 双曲线的标准方程为
(Ⅱ)设A(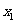 ,
, ),B(
),B( ),P(
),P( ),
),
则 =
= ,
,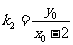 。
。
因为点P在双曲线 上,所以
上,所以 。
。
因此 ,
,
即

同理可 得
得
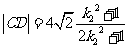 .
.
则
 ,
,
又
 ,
,
所以

 .
.
故

因此
存在 ,使
,使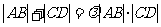 恒成立.
恒成立.
(22)(本小题满分14分)
已知函数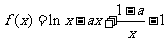
 .
.
(Ⅰ)当 时,讨论
时,讨论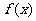 的单调性;
的单调性;
(Ⅱ)设 当
当 时,若对任意
时,若对任意 ,存在
,存在 ,使
,使
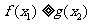 ,求实数
,求实数 取值范围.
取值范围.
[解析](Ⅰ)原函数的定义域为(0,+ ,因为
,因为  =
=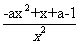 ,所以
,所以
当 时,
时, ,令
,令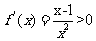 得
得 ,所以
,所以
此时函数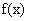 在(1,+
在(1,+ 上是增函数;在(0,1)上是减函数;
上是增函数;在(0,1)上是减函数;
当 时,
时,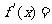


 ,所以
,所以
此时函数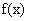 在(0,+
在(0,+ 是减函数;
是减函数;
当 时,令
时,令 =
=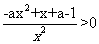 得
得 ,解得
,解得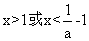 (舍去),此时函数
(舍去),此时函数
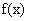 在(1,+
在(1,+ 上是增函数;在(0,1)上是减函数;
上是增函数;在(0,1)上是减函数;
当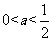 时,令
时,令 =
=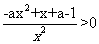 得
得 ,解得
,解得 ,此时函数
,此时函数
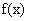 在(1,
在(1, 上是增函数;在(0,1)和
上是增函数;在(0,1)和 +
+ 上是减函数;
上是减函数;
当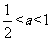 时,令
时,令 =
=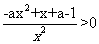 得
得 ,解得
,解得 ,此时函数
,此时函数
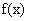 在
在 1)上是增函数;在(0,
1)上是增函数;在(0, )和
)和 +
+ 上是减函数;
上是减函数;
当 时,由于
时,由于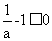 ,令
,令 =
=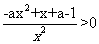 得
得 ,可解得0
,可解得0 ,此时函数
,此时函数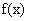 在(0,1)上是增函数;在(1,+
在(0,1)上是增函数;在(1,+ 上是减函数。
上是减函数。
(Ⅱ)当 时,
时,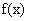 在(0,1)上是减函数,在(1,2)上是增函数,所以对任意
在(0,1)上是减函数,在(1,2)上是增函数,所以对任意 ,
,
有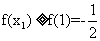 ,又已知存在
,又已知存在 ,使
,使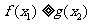 ,所以
,所以 ,
, ,
,
即存在 ,使
,使 ,即
,即 ,即
,即
 ,
,
所以 ,解得
,解得 ,即实数
,即实数 取值范围是
取值范围是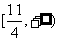 。
。
[命题意图]本题将导数、二次函数、不等式知识有机的结合在一起,考查了利用导数研究函数的单调性、利用导数求函数的最值以及二次函数的最值问题,考查了同学们分类讨论的数学思想以及解不等式的能力;考查了学生综合运用所学知识分析问题、解决问题的能力。
(1)直接利用函数与导数的关系讨论函数的单调性;(2)利用导数求出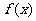 的最小值、利用二次函数知识或分离常数法求出
的最小值、利用二次函数知识或分离常数法求出 在闭区间[1,2]上的最大值,然后解不等式求参数。
在闭区间[1,2]上的最大值,然后解不等式求参数。
(标准答案)(22)本小题主要考查导数的概念以及利用导数研究函数性质的能力,考查分类讨论思想、数形结合思想、等价变换思想,以及综合运用知识解决新情境、新问题的能力。
解:(Ⅰ)因为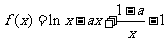 ,
,
所以 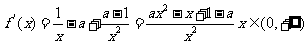 ,
,
令  ,
,

①当 时,
时, 恒成立,此时
恒成立,此时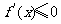 ,函数
,函数 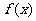 在
在 上单调递减;
上单调递减;
②当 ,
,
 时,
时, ,此时
,此时 ,函数
,函数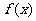 单调递减;
单调递减;
 时
时 ,此时
,此时 ,函数
,函数 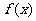 单调递增;
单调递增;
 时,
时, ,此时
,此时 ,函数
,函数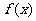 单调递减;
单调递减;
③当 时,由于
时,由于 ,
,
 ,
, ,此时
,此时 ,函数
,函数 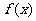 单调递减;
单调递减;
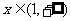 时,
时, ,此时
,此时 ,函数
,函数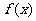 单调递增.
单调递增.
综上所述:

(Ⅱ)因为a=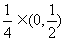 ,由(Ⅰ)知,
,由(Ⅰ)知,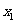 =1,
=1,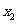 =3
=3 ,当
,当 时,
时, ,函数
,函数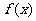 单调递减;
单调递减; 当
当 时,
时,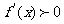 ,函数
,函数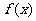 单调递增,所以
单调递增,所以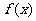 在(0,2)上的最小值为
在(0,2)上的最小值为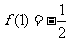 。
。
由于“对任意 ,存在
,存在 ,使
,使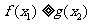 ”等价于
”等价于
“ 在
在 上的最小值不大于
上的最小值不大于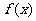 在(0,2)上的最小值
在(0,2)上的最小值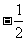 ”(*)
”(*)
又 =
= ,
, ,所以
,所以
①当 时,因为
时,因为 ,此时与(*)矛盾
,此时与(*)矛盾
②当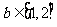 时,因为
时,因为 ,同样与(*)矛盾
,同样与(*)矛盾
③当 时,因为
时,因为 ,解不等式8-4b
,解不等式8-4b ,可得
,可得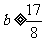
综上,b的取值范围是 。
。
 (13)执行右图所示的程序框图,若输入
(13)执行右图所示的程序框图,若输入 ,则输出
,则输出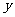 的值为
.
的值为
.
[答案]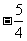
[解析]当x=10时,y= ,此时|y-x|=6;
,此时|y-x|=6;
当x=4时,y=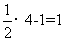 ,此时|y-x|=3;当x=1时,y=
,此时|y-x|=3;当x=1时,y= ,此时|y-x|=
,此时|y-x|= ;
;
当x=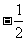 时,y=
时,y= ,此时|y-x|=
,此时|y-x|=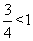 ,故输出y的值为
,故输出y的值为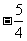 。
。
[命题意图]本题考查程序框图的基础知识,考查了同学们的试图能力。
(14)若对任意 ,
, 恒成立,则
恒成立,则 的取值范围是
.
的取值范围是
.
[答案]
[解析]因为 ,所以
,所以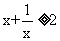 (当且仅当
(当且仅当 时取等号),所以有
时取等号),所以有
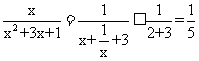 ,即
,即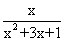 的最大值为
的最大值为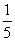 ,故
,故 。
。
[命题意图]本题考查了分式不等式恒成立问题以及参数问题的求解,考查了同学们的转化能力。属中档题。
(15)在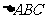 中,角
中,角 所对的边分别为a,b,c,若
所对的边分别为a,b,c,若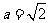 ,
, ,
, ,则角
,则角 的大小为
的大小为
 .
.
[答案]
[解析]由 得
得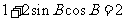 ,即
,即 ,因为
,因为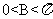 ,所以
,所以
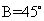 ,又因为
,又因为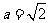 ,
, ,所以在
,所以在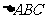 中,由正弦定理得:
中,由正弦定理得: ,解得
,解得
 ,又
,又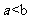 ,所以
,所以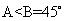 ,所以
,所以 。
。
[命题意图]本题考查了三角恒等变换、已知三角函数值求解以及正弦定理,考查了同学们解决三角形问题的能力,属于中档题。
(16)已知圆C过点(1,0),且圆心在x轴的正半轴上,直线 :
: 被圆C所截得的弦长为
被圆C所截得的弦长为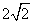 ,则过圆心且与直线
,则过圆心且与直线 垂直的直线的方程为
.
垂直的直线的方程为
.
[答案]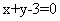
[解析]由题意,设所求的直线方程为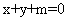 ,设圆心坐标为
,设圆心坐标为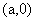 ,则由题意知:
,则由题意知:
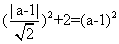 ,解得
,解得 或-1,又因为圆心在x轴的正半轴上,所以
或-1,又因为圆心在x轴的正半轴上,所以 ,故圆心坐标为
,故圆心坐标为
(3,0),因为圆心(3,0)在所求的直线上,所以有 ,即
,即 ,故所求的直线方程为
,故所求的直线方程为
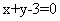 。
。
[命题意图]本题考查了直线的方程、点到直线的距离、直线与圆的关系,考查了同学们解决直线与圆问题的能力。
有一项是满足题目要求的.
(1)
已知全集U=R,集合M={x||x-1| 2},则
2},则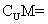
(A){x|-1<x<3} (B){x|-1 x
x 3} (C){x|x<-1或x>3}
(D){x|x
3} (C){x|x<-1或x>3}
(D){x|x -1或x
-1或x 3}
3}
[答案]C
[解析]因为集合
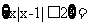
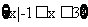 ,全集
,全集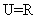 ,所以
,所以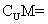
 ,故选C.
,故选C.
[命题意图]本题考查集合的补集运算,属容易题.
(2)
已知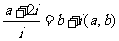
 (a,b∈R),其中i为虚数单位,则a+b=
(a,b∈R),其中i为虚数单位,则a+b=
(A)-1 (B)1 (C)2 (D)3
[答案]B
[解析]由 得
得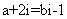 ,所以由复数相等的意义知:
,所以由复数相等的意义知: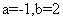 ,所以
,所以 1,故选B.
1,故选B.
[命题意图]本题考查复数相等的意义、复数的基本运算,属保分题。
(3)在空间,下列命题正确的是
(A)平行直线的平行投影重合
( B)平行于同一直线的两个平面平行
B)平行于同一直线的两个平面平行
(C)垂直于同一平面的两个平面平行
(D)垂直于同一平面的两条直线平行
[答案]D
[解析]由空间直线与平面的位置关系及线面垂直与平行的判定与性质定理可以很容易得出答案。
[命题意图]本题考查空间直线与平面的位置关系及线面垂直与平行的判定与性质,属基础题。
(4)设f(x)为定义在R上的奇函数,当x≥0时,f(x)= +2x+b(b为常数),则f(-1)=
+2x+b(b为常数),则f(-1)=
(A) 3 (B) 1 (C)-1 (D)-3
[答案]D
[解析]因为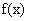 为定义在R上的奇函数,所以有
为定义在R上的奇函数,所以有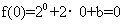 ,解得
,解得 ,所以
,所以
当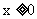 时,
时,  ,即
,即
 ,故选D.
,故选D.
[命题意图]本题考查函数的基本性质,熟练函数的基础知识是解答好本题的关键.
(5)已知随机变量Z服从正态分布N(0, ),若P(Z>2)=0.023,则P(-2≤Z≤2)=
),若P(Z>2)=0.023,则P(-2≤Z≤2)=
(A)0.477
(B)0.625
(C)0.954 (D)0.9 77
77
[答案]C
[解析]因为随机变量 服从正态分布
服从正态分布 ,所以正态曲线关于直线
,所以正态曲线关于直线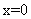 对称,又
对称,又 ,所以
,所以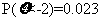 ,所以
,所以

 0.954,故选C.
0.954,故选C.
[命题意图]本题考查正态分布的基础知识,掌握其基础知识是解答好本题的关键.
(6)样本中共有五个个体,其值分别为a,0,1,2,3,,若该样本的平均值为1,则样本方差为
(A) 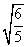 (B)
(B)  (C)
(C)
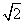 (D)2
(D)2
[答案]D
[解析]由题意知 ,解得
,解得 ,所以样本方差为
,所以样本方差为
 =2,故选D.
=2,故选D.
[命题意图]本题考查用样本的平均数、方差来估计总体的平均数、方差,属基础题,熟记样本的平均数、方差公式是解答好本题的关键.
(7)由曲线y= ,y=
,y= 围成的封闭图形面积为
围成的封闭图形面积为
(A) (B)
(B)
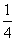 (C)
(C) 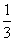 (D)
(D)

[答案]A
[解析]由题意得:所求封闭图形的面积为
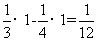 ,故选A。
,故选A。
[命题意图]本题考查定积分的基础知识,由定积分求曲线围成封闭图形的面积。
(8)某台小型晚会由6个节目组成,演出顺序有如下要求:节目甲必须排在第四位、节目乙不能排在第一位,节目丙必须排在最后一位,该台晚会节目演出顺序的编排方案共有
 (A)36种 (B)42种 (C)48种 (D)54种
(A)36种 (B)42种 (C)48种 (D)54种
[答案]B
[解析]分两类:第一类:甲排在第一位,共有 种排法;第二类:甲排在第二位,共有
种排法;第二类:甲排在第二位,共有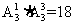 种排法,所以共有编排方案
种排法,所以共有编排方案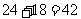 种,故选B。
种,故选B。
[命题意图]本题考查排列组合的基础知识,考查分类与分步计数原理。
(9)设{an}是等比数列,则“a1<a2<a3”是数列{an}是递增数列的
(A)充分而不必要条件 (B)必要而不充分条件、
(C)充分必要条件 (D)既不充分也不必要条件
[答案]C
[解析]若已知 ,则设数列
,则设数列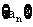 的公比为
的公比为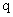 ,因为
,因为 ,所以有
,所以有 ,解得
,解得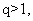 且
且 ,所以数列
,所以数列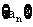 是递增数列;反之,若数列
是递增数列;反之,若数列 是递增数列,则公比
是递增数列,则公比 且
且 ,所以
,所以 ,即
,即 ,所以
,所以 是数列
是数列 是递增数列的充分必要条件。
是递增数列的充分必要条件。
[命题意图]本题考查等比数列及充分必要条件的基础知识,属保分题。
 (10)设变量x、y满足约束条件
(10)设变量x、y满足约束条件 ,则目标函数z=3x-4y的最大值和最小值分别为
,则目标函数z=3x-4y的最大值和最小值分别为
(A)3,-11 (B) -3, -11
(C)11, -3 (D)11,3
[答案]A
[解析]画出平面区域如图所示:
可知当直线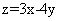 平移到点(5,3)时,目标函数
平移到点(5,3)时,目标函数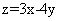 取得最大值3;当直线
取得最大值3;当直线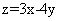 平移到点(3,5)时,目标函数
平移到点(3,5)时,目标函数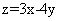 取得最小值-11,故选A。
取得最小值-11,故选A。
[命题意图]本题考查不等式中的线性规划知识,画出平面区域与正确理解目标函数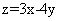 的几何意义是解答好本题的关键。
的几何意义是解答好本题的关键。
(1 1)函数y=2x
1)函数y=2x  -
- 的图像大致是
的图像大致是

[答案]A
[解析]因为当x=2或4时,2x  -
- =0,所以排除B、C;当x=-2时,2x
=0,所以排除B、C;当x=-2时,2x  -
- =
= ,故排除D,所以选A。
,故排除D,所以选A。
[命题意图]本题考查函数的图象,考查同学们对函数基础知识的把握程度以及数形结合的思维能力。
(12)定义平面向量之间的一种运算“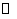 ”如下,对任意的
”如下,对任意的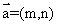 ,
, ,令
,令
 ,下面说法错误的是( )
,下面说法错误的是( )
A.若 与
与 共线,则
共线,则 B.
B.
C.对任意的 ,有
,有
 D.
D. 
[答案]B
[解析]若 与
与 共线,则有
共线,则有 ,故A正确;因为
,故A正确;因为 ,而
,而
 ,所以有
,所以有 ,故选项B错误,故选B。
,故选项B错误,故选B。
[命题意图]本题在平面向量的基础上,加以创新,属创新题型,考查平面向量的基础知识以及分析问题、解决问题的能力。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com