
8.分子式为 的同分异构体共有(不考虑立体异构)
的同分异构体共有(不考虑立体异构)
A.3种 B.4种 C.5种D.6种
一项是符合题目要求的。
7.下列各项表达中正确的是

A.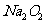 的电子式为
的电子式为
B. 的乙醇和丙醇混合液完全燃烧生成的
的乙醇和丙醇混合液完全燃烧生成的 为
为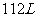 (标准状况)
(标准状况)
C.在氮原子中,质子数为7而中子数不一定为7

(15)(本小题共13分)
已知函数
 。
。
(Ⅰ)求 的值;
的值;
(Ⅱ)求 的最大值和最小值。
的最大值和最小值。
15
(I)

(2)
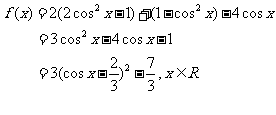
因为 所以当
所以当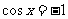 时,
时, 取最大值6;当
取最大值6;当 时,取最小值
时,取最小值 。
。
(16)(本小题共14分)
 如图,正方形ABCD和四边形ACEF所在的平面互相垂直,CE⊥AC,EF∥AC,AB=
如图,正方形ABCD和四边形ACEF所在的平面互相垂直,CE⊥AC,EF∥AC,AB= ,CE=EF=1.
,CE=EF=1.
(Ⅰ)求证:AF∥平面BDE;
(Ⅱ)求证:CF⊥平面BDE;
(Ⅲ)求二面角A-BE-D的大小。
16 证明:(I)设AC与BD交于点G,因为EF∥AG,且EF=1,AG=
证明:(I)设AC与BD交于点G,因为EF∥AG,且EF=1,AG= AC=1,所以四边形AGEF为平行四边形。所以AF∥EG。因为EG
AC=1,所以四边形AGEF为平行四边形。所以AF∥EG。因为EG P平面BDE,AF
P平面BDE,AF 平面BDE,所以AF∥平面BDE。
平面BDE,所以AF∥平面BDE。
 (II)因为正方形ABCD和四边形ACEF所在的平面互相垂直,且CE⊥AC,所以CE⊥AC,所以CE⊥平面ABCD。如图,以C为原点,建立空间直角坐标系C-xyz。则C(0, 0, 0),A(
(II)因为正方形ABCD和四边形ACEF所在的平面互相垂直,且CE⊥AC,所以CE⊥AC,所以CE⊥平面ABCD。如图,以C为原点,建立空间直角坐标系C-xyz。则C(0, 0, 0),A( ,
, ,0),D(
,0),D( ,0, 0),E(0, 0, 1),F(
,0, 0),E(0, 0, 1),F( ,
, ,1)。所以
,1)。所以 =(
=( ,
, ,1),
,1), =(0,-
=(0,- ,1),
,1), =(-
=(- ,0,1)。所以
,0,1)。所以 ·
· =
0-1+1=0,
=
0-1+1=0, ·
· =-1+0+1=0。所以CF⊥BE,CF⊥DE,所以CF⊥平面BDE
=-1+0+1=0。所以CF⊥BE,CF⊥DE,所以CF⊥平面BDE
(III)由(II)知, =(
=( ,
, ,1),是平面BDE的一个法向量,设平面ABE的法向量
,1),是平面BDE的一个法向量,设平面ABE的法向量 =(x,y,z),则
=(x,y,z),则 ·
· =0,
=0, ·
· =0。
=0。
即
所以x=0,且z= y。令y=1,则z=
y。令y=1,则z= 。所以n=(
。所以n=( ),从而cos(
),从而cos( ,
, )=
)=
因为二面角A-BE-D为锐角,所以二面角A-BE-D为 。
。
(17)(本小题共13分)
某同学参加3门课程的考试。假设该同学第一门课程取得优秀成绩的概率为 ,第二、第三门课程取得优秀成绩的概率分别为
,第二、第三门课程取得优秀成绩的概率分别为 ,
, (
( >
> ),且不同课程是否取得优秀成绩相互独立。记ξ为该生取得优秀成绩的课程数,其分布列为
),且不同课程是否取得优秀成绩相互独立。记ξ为该生取得优秀成绩的课程数,其分布列为
|
ξ |
0 |
1 |
2 |
3 |
|
P |
 |
 |
b |
 |
(Ⅰ)求该生至少有1门课程取得优秀成绩的概率;
(Ⅱ)求 ,
, 的值;
的值;
(Ⅲ)求数学期望 ξ。
ξ。
17
解:事件A,表示“该生第i门课程取得优异成绩”,i=1,2,3。由题意可知
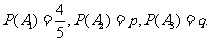
(I)由于事件“该生至少有一门课程取得优异成绩”与事件“ ”是对立的,所以该生至少有一门课程取得优秀成绩的概率是
”是对立的,所以该生至少有一门课程取得优秀成绩的概率是

(II)由题意可知,

整理得pq= 。
。
(III)由题意知,

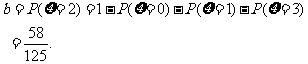

(18)(本小题共13分)
已知函数
(Ⅰ)当 =2时,求曲线
=2时,求曲线 =
= (
(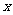 )在点(1,
)在点(1,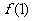 )处的切线方程;
)处的切线方程;
(Ⅱ)求 (
(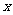 )的单调区间。
)的单调区间。
18
解:(I)当 时,
时, 
由于 所以曲线
所以曲线 处的切线方程为
处的切线方程为
 。即
。即
(II)
当 时,
时,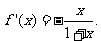
因此在区间 上,
上, ;在区间
;在区间 上,
上, ;
;
所以 的单调递增区间为
的单调递增区间为 ,单调递减区间为
,单调递减区间为 ;
;
当 时,
时, ,得
,得 ;
;
因此,在区间 和
和 上,
上, ;在区间
;在区间 上,
上, ;
;
即函数  的单调递增区间为
的单调递增区间为 和
和 ,单调递减区间为
,单调递减区间为 ;
;
当 时,
时, .
. 的递增区间为
的递增区间为
当 时,由
时,由 ,得
,得 ;
;
因此,在区间 和
和 上,
上, ,在区间
,在区间 上,
上, ;
;
即函数  的单调递增区间为
的单调递增区间为 和
和 ,单调递减区间为
,单调递减区间为 。
。
(19)(本小题共14分)
在平面直角坐标系xOy中,点B与点A(-1,1)关于原点O对称,P是动点,且直线AP与BP的斜率之积等于 .
.
(Ⅰ)求动点P的轨迹方程;
(Ⅱ)设直线AP和BP分别与直线x=3交于点M,N,问:是否存在点P使得△PAB与△PMN的面积相等?若存在,求出点P的坐标;若不存在,说明理由。
19,
解:(1)因点B与(-1,1)关于原点对称,得B点坐标为(1,-1)。
设P点坐标为 ,则
,则 ,由题意得
,由题意得 ,
,
化简得: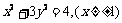 。
。
即P点轨迹为: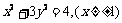
(2)因 ,可得
,可得 ,
,
又 ,
,
若 ,则有
,则有 , 即
, 即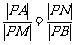
设P点坐标为 ,则有:
,则有:
解得: ,又因
,又因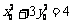 ,解得
,解得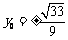 。
。
故存在点P使得 与
与 的面积相等,此时P点坐标为
的面积相等,此时P点坐标为 或
或
(20)(本小题共13分)
已知集合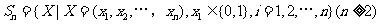 对于
对于 ,
, ,定义A与B的差为
,定义A与B的差为

A与B之间的距离为
(Ⅰ)证明: ,且
,且 ;
;
(Ⅱ)证明: 三个数中至少有一个是偶数
三个数中至少有一个是偶数
(Ⅲ) 设P ,P中有m(m≥2)个元素,记P中所有两元素间距离的平均值为
,P中有m(m≥2)个元素,记P中所有两元素间距离的平均值为 .
.
证明: ≤
≤ .
.
20,
[分析]:这道题目的难点主要出现在读题上,这里简要分析一下。
题目所给的条件其实包含两个定义,第一个是关于 的,其实
的,其实 中的元素就是一个n维的坐标,其中每个坐标值都是0或者1,
也可以这样理解,就是一个n位数字的数组,每个数字都只能是0和1,
第二个定义叫距离,距离定义在两者之间,如果直观理解就是看两个数组有多少位不同,因为只有0和1才能产生一个单位的距离,因此这个大题最核心的就是处理数组上的每一位数,然后将处理的结果综合起来,就能看到整体的性质了。
中的元素就是一个n维的坐标,其中每个坐标值都是0或者1,
也可以这样理解,就是一个n位数字的数组,每个数字都只能是0和1,
第二个定义叫距离,距离定义在两者之间,如果直观理解就是看两个数组有多少位不同,因为只有0和1才能产生一个单位的距离,因此这个大题最核心的就是处理数组上的每一位数,然后将处理的结果综合起来,就能看到整体的性质了。
第一问,因为每个数位上都是0或者1,取差的绝对值仍然是0或者1,符合 的要求。然后是减去C的数位,不管减去的是0还是1,
每一个a和每一个b都是同时减去的,因此不影响他们原先的差。
的要求。然后是减去C的数位,不管减去的是0还是1,
每一个a和每一个b都是同时减去的,因此不影响他们原先的差。
第二问,先比较A和B有几个不同(因为距离就是不同的有几个),然后比较A和C有几个不同,这两者重复的(就是某一位上A和B不同,A和C不同,那么这一位上B和C就相同)去掉两次(因为在前两次比较中各计算了一次),剩下的就是B和C的不同数目,很容易得到这样的关系式: ,从而三者不可能同为奇数。
,从而三者不可能同为奇数。
第三问,首先理解P中会出现 个距离,所以平均距离就是距离总和再除以
个距离,所以平均距离就是距离总和再除以 ,而距离的总和仍然可以分解到每个数位上,第一位一共产生了多少个不同,第二位一共产生了多少个不同,如此下去,直到第n位。然后思考,第一位一共m个数,只有0和1会产生一个单位距离,因此只要分开0和1的数目即可,等算出来
,而距离的总和仍然可以分解到每个数位上,第一位一共产生了多少个不同,第二位一共产生了多少个不同,如此下去,直到第n位。然后思考,第一位一共m个数,只有0和1会产生一个单位距离,因此只要分开0和1的数目即可,等算出来 一切就水到渠成了。
一切就水到渠成了。
此外,这个问题需要注意一下数学语言的书写规范。
解:(1)设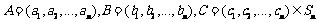
因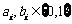 ,故
,故 ,
,
即
又
当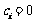 时,有
时,有 ;
;
当 时,有
时,有
故
(2)设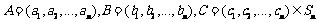
记
记 ,由第一问可知:
,由第一问可知:



即 中1的个数为k,
中1的个数为k, 中1的个数为l,
中1的个数为l,
设t是使 成立的i的个数,则有
成立的i的个数,则有 ,
,
由此可知, 不可能全为奇数,即
不可能全为奇数,即 三个数中至少有一个是偶数。
三个数中至少有一个是偶数。
(3)显然P中会产生 个距离,也就是说
个距离,也就是说 ,其中
,其中 表示P中每两个元素距离的总和。
表示P中每两个元素距离的总和。
分别考察第i个位置,不妨设P中第i个位置一共出现了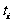 个1,
那么自然有
个1,
那么自然有 个0,因此在这个位置上所产生的距离总和为
个0,因此在这个位置上所产生的距离总和为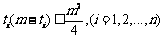 ,
,
那么n个位置的总和
即
下面就一些具体问题来阐述一下解题思路,希望可以指点今后高三学生的一些复习方向。
选择题,第5题,考察知识点:极坐标系,在这个问题的设置上,命题人很巧妙地加入了一个乘积为0的现象,这违背了不少考生在之前的模拟考试中对于极坐标题的认识,认为就是简简单单的坐标转化,这一设置虽未增加多少难度,但构思仍然值得称赞。
选择题,第6题,考察知识点:常用逻辑,向量。借助函数的背景,把几个小知识点灵活地放在一起,若略有粗心便可能失分。
选择题,第7题,考察知识点:线性规划,指数函数。同样是求参数范围,这道题却能突破常规,最大值是3容易想,所有的a大于1却需要学生敏锐的观察力。
选择题,第8题,考察知识点:立体几何。四个运动的点会让考生感觉不太舒服,而几何的美妙之处很大程度上就在于如何从运动中寻找不变,这也是一向北京市命题风格,09年的选择题最后一题也体现了这个风格。
填空题,第14题,一个正方形的滚动虽然是新背景,但也不是第一次在考试中见到,但是这样的滚动方式还是会让不少学生感觉陌生,如何迅速地考察运动状态的每一次变化,就成为了解决这个问题的关键。
解答题整体难度梯度较好,第15题直接考察三角函数虽然有些出人意外,但题目本身中规中矩,跟平时三角函数的练习并没有太大区别,立体几何,概率,导数三道大题也依然维持常态,与我们平时在课堂上讲解的东西保持一致。值得说的是最后两道大题。
19题为解析几何大题,第二问很多考生反映说计算量很大,的确,如果按照一般的计算交点然后计算距离的方式去求三角形面积,计算量的确不小,但是这样做的同学大多数都是拿到题目,未详细思考直接动笔运算,事实上,如果认真考察两个三角形之间的关系,便可以发现这道题目并不需要过于复杂的运算,我后面给出的解法口算即可完成。
最后一题的立意继承了07年的压轴题立意,在离散情况下处理集合的新背景规则,带有一些组合技巧。考生的瓶颈在于读题上,大多数同学读到复杂的符号和定义的时候便头晕眼花,这说明了许多考生对于数学语言的理解层面尚浅,不能将抽象的符号语言转化为直观的认识,北京近年来的压轴题风格多为此类,下一届的高三应该在这方面多下功夫。
2010年普通高等学校招生全国统一考试
(9)在复平面内,复数 对应的点的坐标为
。
对应的点的坐标为
。
9,(-1,1).
解析:
(10)在△ABC中,若b = 1,c = ,
, ,则a =
。
,则a =
。
10, 1。
解析: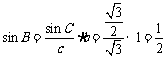 ,因此
,因此 ,故
,故

 (11)从某小学随机抽取100名同学,将他们的身高(单位:厘米)数据绘制成频率分布直方图(如图)。由图中数据可知a=
。若要从身高在[ 120 , 130),[130 ,140) , [140 , 150]三组内的学生中,用分层抽样的方法选取18人参加一项活动,则从身高在[140 ,150]内的学生中选取的人数应为
。
(11)从某小学随机抽取100名同学,将他们的身高(单位:厘米)数据绘制成频率分布直方图(如图)。由图中数据可知a=
。若要从身高在[ 120 , 130),[130 ,140) , [140 , 150]三组内的学生中,用分层抽样的方法选取18人参加一项活动,则从身高在[140 ,150]内的学生中选取的人数应为
。
11,0.030, 3
解析:由所有小矩形面积为1不难得到 ,而三组身高区间的人数比为3:2:1,由分层抽样的原理不难得到140-150区间内的人数为3人。
,而三组身高区间的人数比为3:2:1,由分层抽样的原理不难得到140-150区间内的人数为3人。
(12)如图, 的弦ED,CB的延长线交于点A。若BD
的弦ED,CB的延长线交于点A。若BD AE,AB=4, BC=2, AD=3,则DE=
;CE=
。
AE,AB=4, BC=2, AD=3,则DE=
;CE=
。
12,5,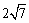
解析:首先由割线定理不难知道 ,于是
,于是 ,又
,又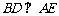 ,故
,故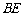 为直径,因此
为直径,因此 ,由勾股定理可知
,由勾股定理可知 ,故
,故
(13)已知双曲线 的离心率为2,焦点与椭圆
的离心率为2,焦点与椭圆 的焦点相同,那么双曲线的焦点坐标为 ;渐近线方程为
。
的焦点相同,那么双曲线的焦点坐标为 ;渐近线方程为
。
13,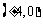 ,
,
解析:双曲线焦点即为椭圆焦点,不难算出为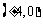 ,又双曲线离心率为2,即
,又双曲线离心率为2,即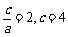 ,故
,故 ,渐近线为
,渐近线为
 (14)如图放置的边长为1的正方形PABC沿
(14)如图放置的边长为1的正方形PABC沿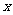 轴滚动。
轴滚动。
设顶点P(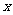 ,y)的轨迹方程是
,y)的轨迹方程是 ,则
,则 的最小正周期为
;
的最小正周期为
; 在其两个相邻零点间的图像与
在其两个相邻零点间的图像与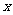 轴
轴
所围区域的面积为 。
说明:“正方形PABC沿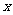 轴滚动”包括沿
轴滚动”包括沿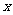 轴正方向和沿
轴正方向和沿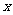 轴负方向滚动。沿
轴负方向滚动。沿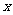 轴正方向滚动指的是先以顶点A为中心顺时针旋转,当顶点B落在
轴正方向滚动指的是先以顶点A为中心顺时针旋转,当顶点B落在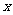 轴上时,再以顶点B为中心顺时针旋转,如此继续。类似地,正方形PABC可以沿
轴上时,再以顶点B为中心顺时针旋转,如此继续。类似地,正方形PABC可以沿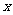 轴负方向滚动。
轴负方向滚动。
14, 4,
解析:不难想象,从某一个顶点(比如A)落在x轴上的时候开始计算,到下一次A点落在x轴上,这个过程中四个顶点依次落在了x轴上,而每两个顶点间距离为正方形的边长1,因此该函数的周期为4。下面考察P点的运动轨迹,不妨考察正方形向右滚动,P点从x轴上开始运动的时候,首先是围绕A点运动 个圆,该圆半径为1,然后以B点为中心,滚动到C点落地,其间是以BP为半径,旋转90°,然后以C为圆心,再旋转90°,这时候以CP为半径,因此最终构成图象如下:
个圆,该圆半径为1,然后以B点为中心,滚动到C点落地,其间是以BP为半径,旋转90°,然后以C为圆心,再旋转90°,这时候以CP为半径,因此最终构成图象如下:


因此不难算出这块的面积为
(1) 集合 ,则
,则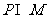 =
=
(A) {1,2} (B) {0,1,2} (C){x|0≤x<3} (D) {x|0≤x≤3}
1,B.
解析: ,
,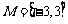 ,因此
,因此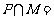
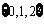
(2)在等比数列 中,
中, ,公比
,公比 .若
.若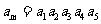 ,则m=
,则m=
 (A)9 (B)10 (C)11
(D)12
(A)9 (B)10 (C)11
(D)12
2,C.
解析: ,因此有
,因此有
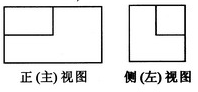
(3)一个长方体去掉一个小长方体,所得几何体的正(主)视图与侧(左)视图分别如右图所示,则该几何体的俯视图为

3,C.
解析:很容易看出这是一个面向我们的左上角缺了一小块长方体的图形,不难选出答案。
(4)8名学生和2位第师站成一排合影,2位老师不相邻的排法种数为
(A) (B)
(B)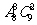 (C)
(C)
 (D)
(D)
4,A.
解析:基本的插空法解决的排列组合问题,将所有学生先排列,有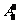 种排法,然后将两位老师插入9个空中,共有
种排法,然后将两位老师插入9个空中,共有 种排法,因此一共有
种排法,因此一共有 种排法。
种排法。
(5)极坐标方程(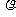 -1)(
-1)( )=0(
)=0(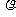
 0)表示的图形是
0)表示的图形是
(A)两个圆 (B)两条直线
(C)一个圆和一条射线 (D)一条直线和一条射线
5,C.
解析:原方程等价于 或
或 ,前者是半径为1的圆,后者是一条射线。
,前者是半径为1的圆,后者是一条射线。
(6)若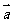 ,
, 是非零向量,“
是非零向量,“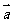 ⊥
⊥ ”是“函数
”是“函数 为一次函数”的
为一次函数”的
(A)充分而不必要条件 (B)必要不充分条件
(C)充分必要条件 (D)既不充分也不必要条件
6,B.
解析: ,如
,如 ,则有
,则有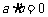 ,如果同时有
,如果同时有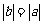 ,则函数恒为0,不是一次函数,因此不充分,而如果
,则函数恒为0,不是一次函数,因此不充分,而如果 为一次函数,则
为一次函数,则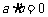 ,因此可得
,因此可得 ,故该条件必要。
,故该条件必要。
(7)设不等式组  表示的平面区域为D,若指数函数y=
表示的平面区域为D,若指数函数y= 的图像上
的图像上
存在区域D上的点,则a 的取值范围是
(A)(1,3]
(B )[2,3] (C )
(1,2]
(D )[ 3,  ]
]
7,A.
解析:这是一道略微灵活的线性规划问题,作出区域D的图象,联系指数函数 的图象,能够看出,当图象经过区域的边界点(2,9)时,a可以取到最大值3,而显然只要a大于1,图象必然经过区域内的点。
的图象,能够看出,当图象经过区域的边界点(2,9)时,a可以取到最大值3,而显然只要a大于1,图象必然经过区域内的点。
 (8)如图,正方体ABCD-
(8)如图,正方体ABCD- 的棱长为2,动点E、F在棱
的棱长为2,动点E、F在棱 上,动点P,Q分别在棱AD,CD上,若EF=1,
上,动点P,Q分别在棱AD,CD上,若EF=1, E=x,DQ=y,DP=z(x,y,z大于零),则四面体PEFQ的体积
E=x,DQ=y,DP=z(x,y,z大于零),则四面体PEFQ的体积
(A)与x,y,z都有关
(B)与x有关,与y,z无关
(C)与y有关,与x,z无关
(D)与z有关,与x,y无关
8,D.
解析:这道题目延续了北京高考近年8,14,20的风格,即在变化中寻找不变,从图中可以分析出, 的面积永远不变,为面
的面积永远不变,为面 面积的
面积的 ,而当
,而当 点变化时,它到面
点变化时,它到面 的距离是变化的,因此会导致四面体体积的变化。
的距离是变化的,因此会导致四面体体积的变化。
第II卷(共110分)
5.标志确定法
有些虚词是构成文言虚词句式的标志词,抓住标志即可事半功倍。如判断句的标志词“者”“也”“乃”等,被动句的标志词“见”“于”“为所”等,宾语前置的标志词“是”“之”等;定语前置的标志词语“者”“之”等。如第1题A项中“句读之不知”中的“之”就是宾语前置的标志。再如,判断句:“廉颇者,赵之良将也”“当立者乃公子扶苏”。被动句:“见笑于大方之家”“若属皆且为所虏”。宾语前置标志:“何罪之有”“唯利是图”“唯马首是瞻”。定语后置句:“求人可使报秦者”“处江湖之远”。
4.结构推断法
一是对称法。文言句子里讲究整齐对称,根据这个特点,可以由一个词的意义和用法来推断另一个词的意义和用法。如“木欣欣以向荣,泉涓涓而始流”中的“以”和“而”用法和意义是相同的,都是表修饰的连词。二是成分法。就是依据虚词在句子中充当的成分进行推断。不同的句子成分决定词语的不同词性和用法。如第2题中的C项“其母上书言于王曰”一句的主语是“母”,“其”作“母”的定语,定语一般由代词充当,因此“其”的义项为“代词,他(赵括)的”。
3.代入验证法
一是直接代入法。即将每个虚词的各种用法分别代入句子里去理解,从而判断正误。如前面第1题C项中的“而”,“而”字的常见义项有:①表并列,②表顺承,③表递进,④表转折,⑤表修饰,将其分别代入,结合语境推断出其用法即可。二是换位代入法。即将同组一个句子中的虚词的意义和用法代入另一个句子理解,看是否讲得通,依此来推断正误。如第1题中的D项“月出于东山之上”很容易推断出“于”的义项是介词“从”,把这种意义和用法代入“人力不至于此”中理解讲不通,依此推断出两组的“而”字意义用法不相同。
2.语境辨析法
即根据上下文语境(包括外部语境)来推断,在整体把握文句意义的基础上来确定某个词语的用法和意义。如前面第1题中“齐人伐燕,胜之”中的“之”,前句的意思是“齐国人讨伐燕国”,“胜之”的意思是“战胜了它”,表结果。因此“之”是代指“燕国”。
1.词性界定法
有些文言词语兼有实词和虚词的双重性质,根据上下文只要是能从词性的角度作出正确的判断,一般就能对词语进行正确的判断。如果一组句子中同一个文言虚词的词性不一样,那么,其用法也肯定不同。例如2009年广东卷第二大题第6小题中“发兵捕之,久不得”和“周怀政之诛,帝怒甚”的两句,前一个“之”是代词,他;后一个“之”是助词,取消句子独立性,不翻译。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com