
22.(本小题满分10分)选修4-1:几何证明选讲
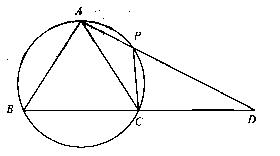
在 中,AB=AC,过点A的直线与其外接圆交于点P,交BC延长线于点D。
中,AB=AC,过点A的直线与其外接圆交于点P,交BC延长线于点D。
 (1)求证:
(1)求证: ;
;
(2)若AC=3,求 的值。
的值。
21.(本小题满分12分)
已知函数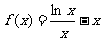
(1)求函数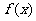 的最大值;
的最大值;
(2)证明:对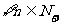 ,不等式
,不等式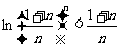 恒成立。
恒成立。
请考生在第22、23、24三题中任选一题作答,如果多做,则按所做的第一题记分。
20.(本小题满分12分)
已知定点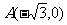 ,B是圆
,B是圆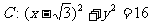 (C为圆心)上的动点,AB的垂直平分线与BC交于点E。
(C为圆心)上的动点,AB的垂直平分线与BC交于点E。
(1)求动点E的轨迹方程;
(2)设直线 与E的轨迹交于P,Q两点,且以PQ为对角线的菱形的一顶点为(-1,0),求斜率
与E的轨迹交于P,Q两点,且以PQ为对角线的菱形的一顶点为(-1,0),求斜率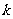 的取值范围。
的取值范围。
19.(本小题满分12分)
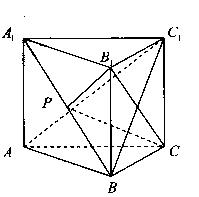 如图,三棱柱ABC-A1B1C1中,侧棱
如图,三棱柱ABC-A1B1C1中,侧棱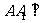 底面ABC,
底面ABC,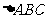 为边长为2的正三角形,点P在A1B上,且AB
为边长为2的正三角形,点P在A1B上,且AB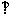 CP。
CP。
(1)证明:P为A1B中点;
(2)若A1B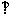 AC1,求三棱锥P-A1AC的体积。
AC1,求三棱锥P-A1AC的体积。
18.(本小题满分12分)
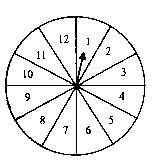
某种日用品上市以后供不应求,为满足更多的消费者,某商场在销售的过程中要求购买这种产品的顾客必须参加如下活动:摇动如图所示的游戏转盘(上面扇形的圆心角都相等),按照指针所指区域的数字购买商品的件数,每人只能参加一次这个活动。
(1)某顾客自己参加活动,购买到不少于5件该产品的概率是多少?
(2)甲、乙两位顾客参加活动,求购买该产品件数之和为10的概率。
17.(本小题满分12分)
2009年11月30时3时许,位于哈尔滨市南岗区东大直街323号的大世界商城发生火灾,为扑灭某着火点,现场安排了两支水枪,如图,D是着火点,A,B分别是水枪位置,已知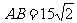 米,在A处看到着火点的仰角为60°,
米,在A处看到着火点的仰角为60°, ,求两支水枪的喷射距离至少是多少?
,求两支水枪的喷射距离至少是多少?
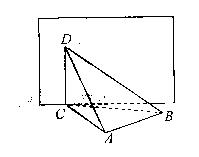
16.已知矩形ABCD,AB=2,BC=1,沿对角线BD将 折起,使二面角C-BD-A为直二面角,则异面直线BC与AD所成角的余弦值为 。
折起,使二面角C-BD-A为直二面角,则异面直线BC与AD所成角的余弦值为 。
15.给定下列四个命题:①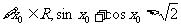 ;②
;②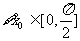 ,
,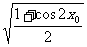 =
=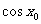 ;③回归方程只适用我们所研究的样本的总体;④用相关指数R2来刻画回归的效果时,R2取值越大,则残差平方和越小,模型拟合的效果就越好,其中为真命题的是
。
;③回归方程只适用我们所研究的样本的总体;④用相关指数R2来刻画回归的效果时,R2取值越大,则残差平方和越小,模型拟合的效果就越好,其中为真命题的是
。
案填在题后的横线上)
|
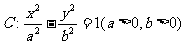 的一条渐近线的方程为
的一条渐近线的方程为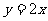 ,则双曲线C的离心率为
。
,则双曲线C的离心率为
。14.如图为一三角形数阵,它满足:
①第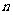 行首尾两数均为
行首尾两数均为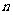 ;②表中的递推关
;②表中的递推关
系类似杨辉三角(三角形数阵中的数为其肩
上两数之和),则第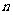 行(
行( )第2个数
)第2个数
是 。
12.定义在R上的函数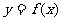 是增函数,且为奇函数,若实数
是增函数,且为奇函数,若实数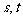 满足不等式
满足不等式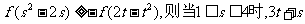 的取值范围是 ( )
的取值范围是 ( )
A.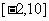 B.
B.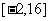
C.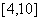 D. [4,16]
D. [4,16]
第Ⅱ卷(非选择题,共90分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com