

2.菜刀在生活中有重要应用。下列情况中,菜刀腐蚀由快到慢的是
①切青菜后用清水冲洗②切湿咸菜后未清洗③切肥猪肉后放置
A.①③② B.②①③ C.③①② D.③②①
1.在我们的日常生活中涉及到许多变化。下列变化中不包含化学变化的是
A.用石灰浆涂抹墙壁后,表面有水珠生成
B.在口中咀嚼米饭或馒头时感到有甜味
C.用干冰做制冷剂进行人工降雨
D.绿色植物的光合作用
(17)(本小题满分10分)(注意:在试题卷上作答无效)
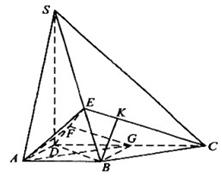
已知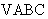 的内角
的内角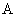 ,
, 及其对边
及其对边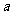
 ,
,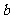
 满足
满足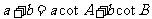 ,求内角
,求内角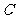 .
.
17. [命题意图]本小题主要考查三角恒等变形、利用正弦、余弦定理处理三角形中的边角关系,突出考查边角互化的转化思想的应用.
[解析]

(18)(本小题满分12分)(注意:在试题卷上作答无效)
投到某杂志的稿件,先由两位初审专家进行评审.若能通过两位初审专家的评审,
则予以录用;若两位初审专家都未予通过,则不予录用;若恰能通过一位初审专家的评
审,则再由第三位专家进行复审,若能通过复审专家的评审,则予以录用,否则不予录
用.设稿件能通过各初审专家评审的概率均为0.5,复审的稿件能通过评审的概率为0.3.
各专家独立评审.
(I)求投到该杂志的1篇稿件被录用的概率;
(II)记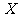 表示投到该杂志的4篇稿件中被录用的篇数,求
表示投到该杂志的4篇稿件中被录用的篇数,求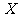 的分布列及期望.
的分布列及期望.
[命题意图]本题主要考查等可能性事件、互斥事件、独立事件、相互独立试验、分布列、数学期望等知识,以及运用概率知识解决实际问题的能力,考查分类与整合思想、化归与转化思想.
[解析](18)解:
(Ⅰ)记 A表示事件:稿件能通过两位初审专家的评审;
B表示事件:稿件恰能通过一位初审专家的评审;
C表示事件:稿件能通过复审专家的评审;
D表示事件:稿件被录用.
则 D=A+B·C,
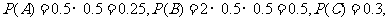
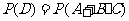
=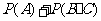
=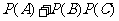
=0.25+0.5×0.3
=0.40.
(Ⅱ)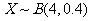 ,其分布列为:
,其分布列为:
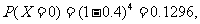
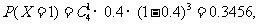
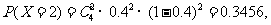
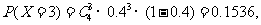
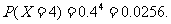
期望 .
.
(19)(本小题满分12分)(注意:在试题卷上作答无效)
如图,四棱锥S-ABCD中,SD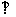 底面ABCD,AB//DC,AD
底面ABCD,AB//DC,AD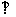 DC,AB=AD=1,DC=SD=2,E为棱SB上的一点,平面EDC
DC,AB=AD=1,DC=SD=2,E为棱SB上的一点,平面EDC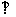 平面SBC .
平面SBC .
(Ⅰ)证明:SE=2EB;
 (Ⅱ)求二面角A-DE-C的大小 .
(Ⅱ)求二面角A-DE-C的大小 .
[命题意图]本小题主要考查空间直线与直线、直线与平面、平面与平面的位置关系,二面角等基础知识,考查空间想象能力、推理论证能力和运算能力.
(19) [解析]解法一:
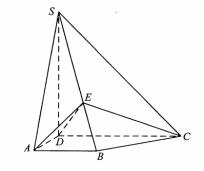
(Ⅰ)连接BD,取DC的中点G,连接BG,
 由此知
由此知  即
即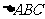 为直角三角形,故
为直角三角形,故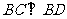 .
.
又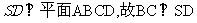 ,
,
所以,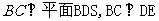 .
.
作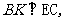
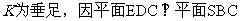 ,
,

(Ⅱ) 由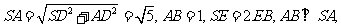 知
知
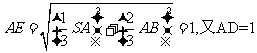 .
.
故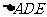 为等腰三角形.
为等腰三角形.
取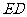 中点F,连接
中点F,连接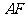 ,则
,则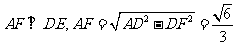 .
.
连接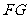 ,则
,则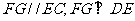 .
.
所 以,
以,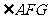 是二面角
是二面角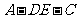 的平面角.
的平面角.
连接AG,A G=
G= ,
,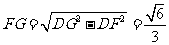 ,
,

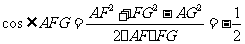 ,
,
所以,二面角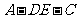 的大小为120°.
的大小为120°.
解法二:
以D为坐标原点,射线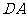 为
为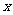 轴的正半轴,建立如图所示的直角坐标系
轴的正半轴,建立如图所示的直角坐标系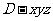 ,
,

由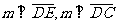 ,得
,得
 ,
,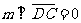
故
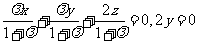 .
.
令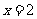 ,则
,则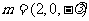 .
.

(20)(本小题满分12分)(注意:在试题卷上作答无效)
已知函数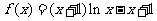 .
.
(Ⅰ)若 ,求
,求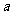 的取值范围;
的取值范围;
(Ⅱ)证明: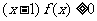 .
.
[命题意图]本小题主要考查函数、导数、不等式证明等知识,通过运用导数知识解决函数、不等式问题,考查了考生综合运用数学知识解决问题的能力以及计算能力,同时也考查了函数与方程思想、化归与转化思想.
[解析]20.解:
(Ⅰ)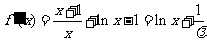 ,
,
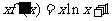 ,
,
题设 等价于
等价于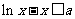 .
.
令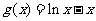 ,则
,则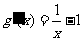
当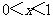 ,
,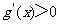 ;当
;当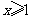 时,
时,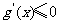 ,
,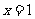 是
是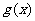 的最大值点,
的最大值点,

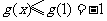
综上,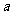 的取值范围是
的取值范围是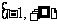 .
.
(Ⅱ)有(Ⅰ)知,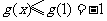 即
即 .
.
当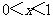 时,
时,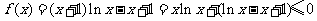 ;
;
当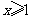 时,
时,
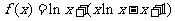

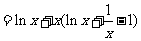
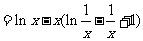
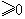
所以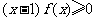
(21)(本小题满分12分)(注意:在试题卷上作答无效)
已知抛物线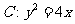 的焦点为F,过点
的焦点为F,过点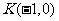 的直线
的直线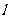 与
与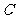 相交于
相交于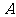 、
、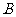 两点,点A关于
两点,点A关于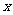 轴的对称点为D .
轴的对称点为D .
(Ⅰ)证明:点F在直线BD上;
(Ⅱ)设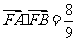 ,求
,求 的内切圆M的方程 .
的内切圆M的方程 .
[命题意图]本小题为解析几何与平面向量综合的问题,主要考查抛物线的性质、直线与圆的位置关系,直线与抛物线的位置关系、圆的几何性质与圆的方程的求解、平面向量的数量积等知识,考查考生综合运用数学知识进行推理论证的能力、运算能力和解决问题的能力,同时考查了数形结合思想、设而不求思想.
[解析](21)解:
设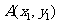 ,
,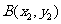 ,
, ,
,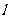 的方程为
的方程为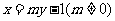 .
.

(Ⅱ)由①知,
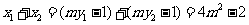
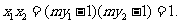
因为 
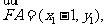
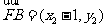 ,
,

故 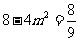 ,
,
解得 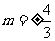
所以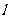 的方程为
的方程为

又由①知 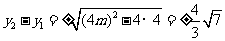
故直线BD的斜率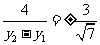 ,
,
因而直线BD的方程为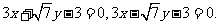
因为KF为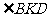 的平分线,故可设圆心
的平分线,故可设圆心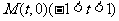 ,
,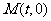 到
到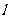 及BD的距离分别为
及BD的距离分别为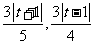 .
.
由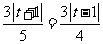 得
得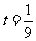 ,或
,或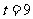 (舍去),
(舍去),
故
圆M的半径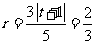 .
.
所以圆M的方程为 .
.
(22)(本小题满分12分)(注意:在试题卷上作答无效)
已知数列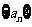 中,
中,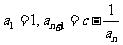 .
.
(Ⅰ)设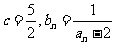 ,求数列
,求数列 的通项公式;
的通项公式;
(Ⅱ)求使不等式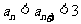 成立的
成立的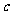 的取值范围 .
的取值范围 .
[命题意图]本小题主要考查数列的通项公式、等比数列的定义、递推数列、不等式等基础知识和基本技能,同时考查分析、归纳、探究和推理论证问题的能力,在解题过程中也渗透了对函数与方程思想、化归与转化思想的考查.
[解析]

(Ⅱ)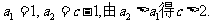
用数学归纳法证明:当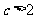 时
时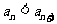 .
.
(ⅰ)当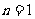 时,
时,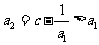 ,命题成立;
,命题成立;

16.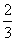
 [命题意图]本小题主要考查椭圆的方程与几何性质、第二定义、平面向量知识,考查了数形结合思想、方程思想,本题凸显解析几何的特点:“数研究形,形助数”,利用几何性质可寻求到简化问题的捷径.
[命题意图]本小题主要考查椭圆的方程与几何性质、第二定义、平面向量知识,考查了数形结合思想、方程思想,本题凸显解析几何的特点:“数研究形,形助数”,利用几何性质可寻求到简化问题的捷径.
[解析]如图,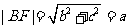 ,
,
作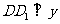 轴于点D1,则由
轴于点D1,则由 ,得
,得
 ,所以
,所以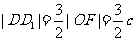 ,
,
即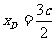 ,由椭圆的第二定义得
,由椭圆的第二定义得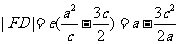
又由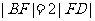 ,得
,得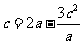 ,整理得
,整理得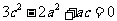 .
.
两边都除以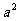 ,得
,得 ,解得
,解得
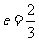 .
.
15.(1,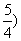 [命题意图]本小题主要考查函数的图像与性质、不等式的解法,着重考查了数形结合的数学思想.
[命题意图]本小题主要考查函数的图像与性质、不等式的解法,着重考查了数形结合的数学思想.
[解析]如图,在同一直角坐标系内画出直线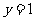 与曲线
与曲线 ,观图可知,a的取值必须满足
,观图可知,a的取值必须满足 解得
解得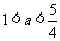 .
.
(16)已知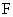 是椭圆
是椭圆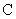 的一个焦点,
的一个焦点, 是短轴的一个端点,线段
是短轴的一个端点,线段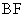 的延长线交
的延长线交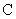 于点
于点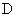 ,且
,且 ,则
,则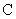 的离心率为
.
的离心率为
.
14.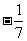 [命题意图]本小题主要考查三角函数值符号的判断、同角三角函数关系、和角的正切公式,同时考查了基本运算能力及等价变换的解题技能.
[命题意图]本小题主要考查三角函数值符号的判断、同角三角函数关系、和角的正切公式,同时考查了基本运算能力及等价变换的解题技能.
[解析]因为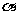 为第三象限的角,所以
为第三象限的角,所以 ,又
,又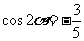 <0, 所以
<0, 所以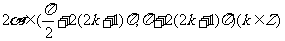 ,于是有
,于是有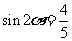 ,
,
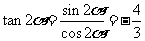 ,所以
,所以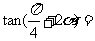
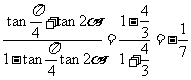 .
.
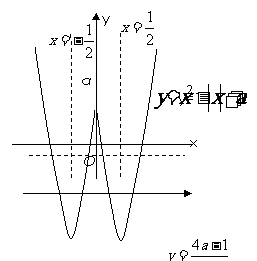 (15)直线
(15)直线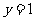 与曲线
与曲线 有四个交点,则
有四个交点,则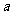 的取值范围是 .
的取值范围是 .
(注意:在试题卷上作答无效)
(13)不等式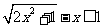 的解集是
.
的解集是
.
13.[0,2] [命题意图]本小题主要考查根式不等式的解法,利用平方去掉根号是解根式不等式的基本思路,也让转化与化归的数学思想体现得淋漓尽致.
解析:原不等式等价于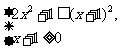 解得0≤x≤2.
解得0≤x≤2.
(14)已知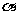 为第三象限的角,
为第三象限的角,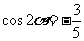 ,则
,则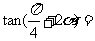 .
.
3。第Ⅱ卷共l0小题,共90分。
2.第Ⅱ卷共2页,请用直径0.5毫米黑色墨水签字笔在答题卡上各题的答题区域
内作答,在试题卷上作答无效。
12.B[命题意图]本小题主要考查几何体的体积的计算、球的性质、异面直线的距离,通过球这个载体考查考生的空间想象能力及推理运算能力.
[解析]过CD作平面PCD,使AB⊥平面PCD,交AB与P,设点P到CD的距离为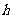 ,则有
,则有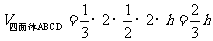 ,当直径通过AB与CD的中点时,
,当直径通过AB与CD的中点时,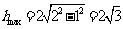 ,故
,故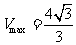 .
.
绝密★启用前
2010年普通高等学校招生全国统一考试
理科数学(必修+选修II)
第Ⅱ卷
证号填写清楚,然后贴好条形码。请认真核准条形码上的准考证号、姓名和科目。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com